Построить отрицание высказывания различными способами

Пример высказывания и его отрицания

Пусть предложение А – высказывание. Если перед сказуемым данного предложения поставить частицу «не» либо перед всем предложением поставить слова «неверно, что», то получится новое предложение, которое называется отрицанием данного и обозначается Ā (читают: «не А» или «неверно, что А).

Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.

Таблица истинности отрицания имеет вид :

А	Ā
и	л
л	и

Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.

Построим отрицание ложного высказывания «число 28 делится на 9:

А) Число 28 не делится на 9.

Б) Неверно, что число 28 делится на 9.

Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.

Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний. Если перед всем составным высказыванием поставим слова «неверно, что», то, безусловно, получим его отрицание. А как быть с частицей «не»? Можно ли поставить перед сказуемым составного предложения и получить его отрицание? На примере можно показать, что нельзя.

Можно доказать, что отрицанием конъюнкции двух высказываний А и В является дизъюнкция их отрицаний. Для этого надо убедиться в том, что значения истинности высказываний вида А∧В и А∨ В совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:

А	В	А∧В	А∧В	А	В	А∨ В
и	и	и	л	л	л	л
и	л	л	и	л	и	и
л	и	л	и	и	л	и
л	л	л	и	и	и	и

Про высказывания вида А∧В и А∨ В говорят, что они равносильны, и пишут

А∧В ⇔ А ∨ В.

Аналогично можно доказать, что имеет место равносильность

А∨В ⇔ А ∧ В.

Эти равносильности носят название законов де Моргана.

Из них вытекает следующее правило построения отрицания конъюнкции и дизъюнкции: чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и).

10. Отношения следования и равносильности между предложениями.

Следование: Рассмотрим две высказывательные формы: «число х кратно 4» и «число х кратно 2», заданные на множестве N натуральных чисел.

Можно сказать так: из того, что число х кратно 4, следует, что хкратно 2, т.к. при всех значениях х, при которых истинно предложение «число х кратно 4», будет истинно и предложение «число х кратно 2». В этом случае говорят, что данные предложения находятся в отношении логического следования.

Определение.Высказывательная форма В(х) следует из высказывательной формы А (х), если В(х) обращается в истинное высказывание при всех тех значениях х, при которых А (х) истинна.

Если А и В – высказывания, тогда говорят, что из А следует В, если всякий раз, когда А истинно, истинно и В.

Для обозначения отношения логического следования используется знак Þ. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) Þ В(х), прочитать которое можно по – разному:

1. Из А(х) следует В(х).

2. Всякое А(х) есть В(х).

3. Если А(х), то В(х).

4. В(х) есть следствие А(х).

5. А(х) есть достаточное условие для В(х).

6. В(х) есть необходимое условие для А(х).

Например, утверждение о том, что из предложения «число х кратно 4», следует предложение «число х кратно 2», можно сформулировать еще так:

– Всякое число, которое кратно 4, кратно и 2.

– Если число кратно 4, то оно кратно и 2.

– Кратность числа 2 есть следствие кратности его 4.

– Кратность числа 4 есть достаточное условие для его кратности 2.

– Кратность числа 2 есть необходимое условие для его кратности 4.

Как и любое высказывание, предложение А(х) Þ В(х) может быть истинным либо ложным. Но так как оно может быть сформулировано в виде «всякое А(х) есть В(х)», то его истинность устанавливается путем доказательства, а с помощью контрпримера – что оно ложно.

Равносильность: Рассмотрим две высказывательные формы А(х) – «число делится на 3» и В(х) – «сумма цифр в записи числа делится на 3». Из школьного курса математики известно, что если число делится на 3, то сумма цифр в записи этого числа разделится на 3, и наоборот. В этом случае говорят, что предложения А(х) и В(х) равносильны.

Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложение В(х), а из предложения В(х) следует предложение А (х).

Для обозначения отношения равносильности используется знак Û. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) Û В(х), прочитать которое можно по-разному:

1. А(х) равносильно В(х).

2. А(х) тогда и только тогда, когда В(х).

3. А(х) – необходимое и достаточное условие для В(х).

4. В(х) – необходимое и достаточное условие для А(х).

Например, утверждение о том, что предложение «число делится на 3» и «сумма цифр в записи числа делится на 3» равносильны, можно сформулировать еще так:

· Число делится на 3 тогда и только тогда, когда сумма цифр вегозаписи делится на 3.

· Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.

В обыденной речи мы очень часто используем частицу «не» или слова «неверно, что», когда что-нибудь отрицаем. В математике также приходится строить предложения, в которых что-либо отрицается.

Например, говоря, что ∆ АВС является непрямоугольным, мы отрицаем, что ∆ АВС – прямоугольный. При этом, отрицая ложное высказывание, получаем истинное, а отрицая истинное высказывание, получаем ложное.

Пусть дано высказывание А. Определим операцию отрицания высказывания.

Отрицанием высказывания А называется высказывание, которое истинно, когда данное высказывание ложно, и ложно, когда данное высказывание истинно.

Отрицание высказывания А обозначается: Ā. Читаем: «не А» или «неверно, что А».

1. А: «3+4=7» – это истинное высказывание. Образуем отрицание данного высказывания.

Ā: «3+4≠7» (три плюс четыре не равно 7»), это будет ложное высказывание.

2. В: «7>9» – это ложное высказывание.

`В: «Неверно, что 7>9» или «7 не больше 9». Слова «не больше» означают «меньше или равно», поэтому в символах `Взапишется: «7≤9», это высказывание истинное.

Определение отрицания высказывания можно записать в так называемой таблице истинности.

Таблицей истинности называется таблица, в которой устанавливается значение истинности составного высказывания при различных комбинациях значений истинности входящих в него элементарных высказываний.

Таблица истинности отрицания высказывания имеет вид:

А	Ā
и л	л и

Пример ознакомления дошкольников с отрицанием «Не А». Наглядный материал изображён на рисунке 15:

яблоко груша апельсин лук

Задание ребенку: «Выбери лишний предмет, объясни, почему ты так думаешь».

Элементарное предложение: А – «предмет фрукт». Составное предложение: «Не А» – «предмет не является фруктом».

Если предложение А – элементарное высказывание, то для построения отрицания следует либо предварить его словами «неверно, что…», либо поставить частицу «не» перед сказуемым (если А содержит частицу «не», то отбросить ее).

Выбор ребенка	Значение истинности элементарных предложений А	Оценка воспитателя
и	«неправильно»
л	«правильно»

Для операции отрицания высказывания А выполняется закон, называемый закономдвойного отрицания:

( А) ( =А).

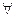
Читаем: «Для любого высказывания А двойное отрицание высказывания А равно высказыванию А».

Доказательство этого закона выполняем в следующей таблице истинности, используя определение отрицания высказывания и определение равносильных высказываний.

А	Ā
и л	л и	и л

Как видно из таблицы, значения истинности высказываний А и по строкам совпадают, поэтому высказывания А и равносильны и равенство А= является верным.

Убедимся в справедливости этого закона и на примерах.

1. А: «Кызыл – столица Тувы» – и;

Ā: «Кызыл не является столицей Тувы» – л;

: «Неверно, что Кызыл не является столицей Тувы» – и.

: «Неверно, что 2³ ≠ 9» – л.

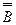
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10803 – | 7379 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Министерство образования и науки РД

ГБПОУ «Профессионально- педагогический колледж имени Р. Гамзатова».

Разработка урока по математике

Тема: Отрицание высказываний.

2015-2016 уч. год.

Тема: Отрицание высказываний.

Цели : Ознакомить с правилами построения отрицаний высказываний ; совершенствовать навыки по определению значений истинности различных математических предложений; развивать навыки логического мышления и интерес к математике.

Оборудование : таблицы, тесты.

Повторение пройденного материала.

Объяснение нового материала.

Закрепление нового материала.

Итоги урока. Домашнее задание.

-Здравствуйте, сегодня мы закрепим знания о конъюнкции и дизъюнкции высказываний, о высказываниях с кванторами и научимся строить отрицания различных видов высказываний.

Повторение пройденного материала.

– Сначала выполним несколько заданий на повторение пройденного материала.

Что называется высказыванием? Что называется высказывательной формой?

а) Среди предложений укажите высказывания и высказывательные формы

В сутках 48 часов.

Почему снег белый?

Число х кратно 2.

Что больше: 5 или 7?

б) Придумайте предложение являющееся высказыванием.

Приведите пример предложений, не являющихся высказываниями.

в) Среди предложений укажите истинное высказывание.

Волга впадает в Черное море.

г) Придумайте два истинных и два ложных высказывания.

д) Верно ли высказывание? Объясните.

Через две точки можно провести несколько прямых.

Уравнение x+7=5 не имеет корней.

Число 4 является корнем уравнения 72:х=18.

Что называется конъюнкцией высказываний? Что называется дизъюнкцией высказываний?

Определите значение истинности высказываний.

Число 16 кратно 2 и нечетное.

Число 20 делится на 3 или на 6.

Квадрат является прямоугольником или трапецией.

Решите систему неравенств и уравнение и покажите связь с конъюнкцией и дизъюнкцией высказывательных форм

4) – Какие различают кванторы?

– Как показать истинность и ложность высказываний с квантором общности?

– Как показать истинность и ложность высказываний с квантором существования?

Существует число, которое делится на 7.

Все четырехугольники – квадраты.

Любое двузначное число больше 5.

Среди прямоугольных треугольников есть равносторонние.

Поставьте вместо многоточия логическую связку «и» или «или», чтобы получилось истинное высказывание

а) Число 18 четное … кратно 9.

б) Прямоугольник является трапецией … параллелограммом.

в) Число 10 делится на 5 … однозначное.

г) Число 12 кратно 2 … 6.

2) Вместо многоточия поставьте квантор, чтобы получилось истинное высказывание

а) … число кратно 5.

б) … прямоугольник является параллелограммом.

в) … натуральное число больше 0.

г) … треугольник является равносторонним.

3) Решите систему неравенств и уравнение и покажите связь с конъюнкцией и дизъюнкцией высказывательных форм, если хϵ R

Поставьте вместо многоточия логическую связку «и» или «или», чтобы получилось истинное высказывание

а) Число 21 меньше 8 … нечетное.

б) Квадрат является ромбом … прямоугольником.

в) Число 18 делится на 3 … больше 5.

г) Трапеция является четырехугольником … квадратом.

2) Вместо многоточия поставьте квантор, чтобы получилось истинное высказывание

а) … равносторонний треугольник является равнобедренным.

б) … число четное.

в) … двузначное число больше 9.

г) … трапеция является равнобокой.

3) Решите систему неравенств и уравнение и покажите связь с конъюнкцией и

дизъюнкцией высказывательных форм, если хϵ R

Объяснение нового материала.

Часто в математике приходится строить отрицания высказыванийй.

Пусть А-высказывание. Если перед сказуемым данного предложения поставить частицу «не», либо перед всем предложением поставить слова «неверно, что», то получится предложение, которое называется отрицанием данного высказывания и обозначается А (читается: «не А» или «неверно, что А»).

Определение: Отрицанием высказывания А называется высказывание А, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А-ложно.

Пример: А: Число 16 делится на 9.

А: а) Число 16 не делится на 9.

б) Неверно, что число 16 делится на 9.

Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний.

Чтобы построить отрицание конъюнкции и дизъюнкции, достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и»).

Это правило можно записать в виде равносильностей А˄В ⇔ А˅В и А˅В ⇔ А˄В.

Эти равносильности называют законами де Моргана.

1) Построить отрицание высказывания: «Число 25 кратно 3 или 5».

Отрицание можно построить двумя способами:

а) Неверно, что число 25 кратно 3 или 5.

б) Число 25 не кратно 3 или 5.

2) Построить отрицание высказывания: «Число 6 четное и делится на 4».

Отрицание можно построить двумя способами.

а) Неверно, что число 6 четное и делится на 4.

б) Число 6 нечетное или не делится на 4.

Теперь рассмотрим правила построения отрицаний высказываний, которые содержат кванторы.

Для того, чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.

Это правило можно записать двумя раносильностями:

( ∀ х) А(х) ⇔ ( ∃ х) А(х) и ( ∃ х) А(х) ⇔ ( ∀ х) А(х)

1) Построить отрицание высказывания: «Некоторые студенты отличники».

Отрицание можно построить двумя способами:

а) Неверно, что некоторые студенты отличники.

б) Всякий студент не отличник.

2) Построить отрицание высказывания: «Все числа больше 10»

Отрицание можно построить двумя способами:

а) Неверно, что все числа больше 10

б) Существуют числа не больше 10

Закрепление нового материала.

Сформулируйте отрицания следующих предложений двумя способами:

Квадрат является ромбом.

а) Неверно, что квадрат является ромбом.

б) Квадрат не является ромбом.

Число 6 однозначное и меньше 8.

а) Неверно, что число 6 однозначное и меньше 8.

б) Число 6 не однозначное или не меньше 8.

Трапеция является параллелограммом или прямоугольником.

а) Неверно, что трапеция является параллелограммом или прямоугольником.

б) Трапеция не является параллелограммом и прямоугольником.

Всякое число четное.

а) Неверно, что всякое число четное.

б) Существует число, которое не является четным.

Хотя бы одно число четное.

а) Неверно, что хотя бы одно число четное.

б) Любое число нечетное.

Итоги урока. Домашнее задание.

Махмудов Алиярбек МахмудовичНаписать 769 04.04.2019

Номер материала: ДБ-538382

04.04.2019 47

04.04.2019 343

04.04.2019 118

04.04.2019 584

04.04.2019 6086

04.04.2019 442

04.04.2019 57

04.04.2019 119

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Источник