Глава 9. Преобразование комплексных чертежей
§ 59. Способ вращения
Как уже отмечалось, при преобразовании комплексного чертежа возможно изменение положения заданных геометрических элементов относительно плоскостей проекций при неизменном положении основных плоскостей проекций. Это осуществляется путем вращения этих элементов вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей. Такое преобразование комплексного чертежа носит название способа вращения .
В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.
При вращении вокруг горизонтально проецирующей прямой горизонтальная проекция А1 точки А перемещается по окружности, а фронтальная А2 — по прямой, перпендикулярной фронтальной проекции оси, являющейся фронтальной проекцией плоскости вращения Г2 (рис. 115).
При этом расстояние между горизонтальными проекциями двух точек А и В (рис. 116) при их повороте на один и тот же угол остается неизменным (A1B1 = A 1 B 1).
Аналогичные выводы можно сделать и для вращения вокруг фронтально проецирующей прямой. При вращении плоской фигуры вокруг оси, перпендикулярной плоскости проекций, проекция ее на эту плоскость не изменяется ни по величине, ни по форме, так как не изменяется наклон плоской фигуры к этой плоскости, а меняется лишь положение этой проекции относительно линии связи. Вторая же проекция на плоскости, параллельной оси вращения, изменяется и по форме, и по величине. Проекции точек на этой плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Пользуясь этими свойствами, можно применить для преобразования чертежа способ вращения, не задаваясь изображением оси вращения и не устанавливая величину радиуса вращения. Это — способ плоскопараллельного перемещения , при котором все точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения действительного вида и размеров этой фигуры (рис. 117).
Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующующмшую в ее плоскости вращения Г ׀׀ П. При этом A1B1C1 = ∆ A 1 B 1 C 1, а плоскости вращения точек В и С параллельны плоскости Г.
Вторым перемещением ∆АВС расположен параллельно плоскости П1. Без изменения оставлена вырожденная фронтальная проекция треугольника ( А 2 В 2 С 2 = А 2 В 2 С 2), а новая горизонтальная проекция, дающая истинную величину ∆АВС поручена построением новых горизонтальных проекций точек A 1, B 1 и С 1 в результате их вращения в параллельных фронтальных плоскостях уровня ( В 2 ∈ Ф; В ∈ Ф).
На этом примере построено решение третьей и четвертой исходных задач путем преобразования комплексного чертежа плоскости общего положения способом плоскопараллельного перемещения.
Если в качестве оси вращения взять линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, т.е. избежать двойного преобразования чертежа, что имело место в замене плоскостей проекций и плос-копараллельномперемещении. На рис. 118 построено изображение ∆АВС ( A 1 B 1 C 1) после поворота его вокруг горизонтали h(C, 1) уровня Г ∈ h.
Так как горизонталь проходит через точку С, то последняя неподвижна при вращении треугольника. Нужно повернуть только точки А и В вокруг горизонтали до совмещения с плоскостью Г ׀׀ П1. Точка А вращается в горизонтально проецирующей плоскости Σ A , перпендикулярной оси вращения. Центр вращения 0 точки А лежит на оси вращения. В момент, когда в результате вращения точка А окажется в плоскости Г, т. е. совместится с горизонтальной плоскостью уровня, ее горизонтальная проекция A 1 будет удалена от горизонтальной проекции оси вращения h1 на расстояние, равное истинной величине радиуса вращения R A точки А. Натуральную величину R A можно построить как гипотенузу О1А прямоугольного треугольника (см. § 42), одним катетом которого является горизонтальная проекция радиуса А1О1, а вторым — разность высот точек А и О. Построив совмещенную горизонтальную проекцию точки А, легко достроить изображение всего треугольника А1В1С1 в совмещенном с плоскостью /положении, используя неподвижную точку и плоскость вращения точки В (Σ1 B ⊥ h1). Фронтальная проекция ∆АВС выродится в прямую и совместится с проекцией Г2 плоскости совмещения.
Аналогичные действия выполняют при вращении плоской фигуры вокруг ее фронтали. Совмещение в этом случае ведется с фронтальной плоскостью уровня (Ф ׀׀ П2), проходящей через ось вращения — фронталь.
Способом вращения могут быть решены и другие задачи, применительно к их условиям.



© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Источник
Задача № 5
По заданным в таблице координатам построить наглядное изображение и эпюр точки. Для каждой точки построить отдельный чертеж. Ось оу проводим под углом 45 0 к горизонтали и откладываем на ней размеры в 2 раза меньше заданного в таблице размера. При построении ортогональных проекций точек размеры откладываем в натуральную величину.
| 1. А | 2. В | 3. С | 4.Д | ||||||||||||
| № | х | у | z | № | х | у | z | № | х | у | z | № | х | у | z |
Задача № 6* и образец ее решения.
Дать наглядные изображения точек А, В, С, D Относительно плоскостей V и H. Точки заданы своими проекциями (рис. а).
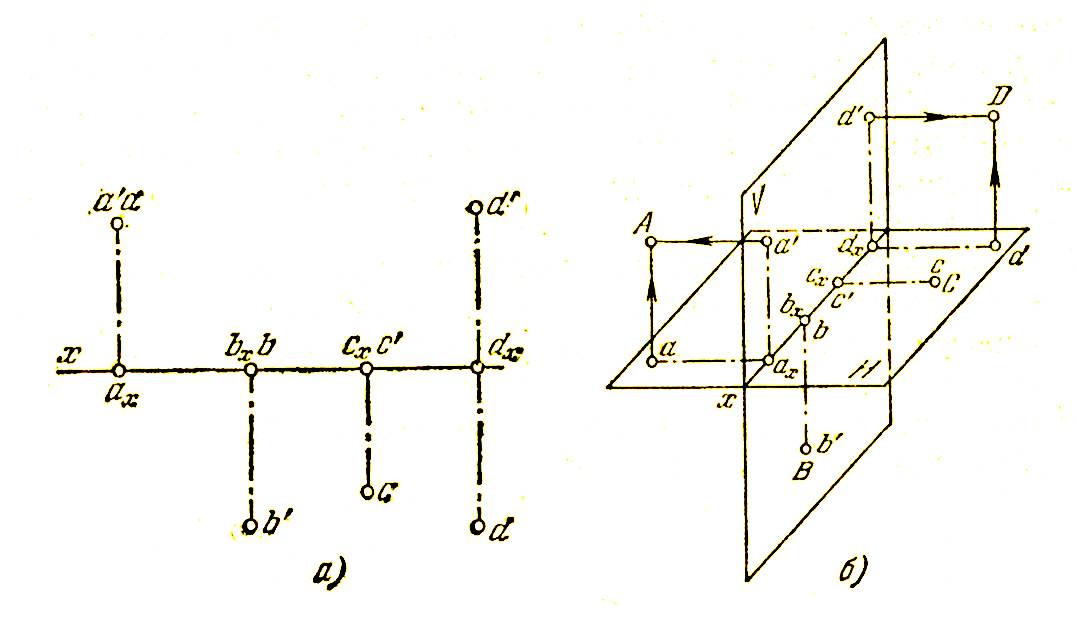 |
Решение: Точки ах, вх, сх, dх ( рис. б) выбираем на оси х произвольно. Так как точка А находится во второй четверти (аппликата точки положительна, ордината отрицательна), то отрезок аха, соответствующий значению ординаты откладываем влево от плоскости V . Отрезок аха‘, соответствующий значению аппликаты, откладываем вверх от плоскости Н.
Для построения точки D, находящейся в первой четверти (аппликата и ордината положительны), отрезок dxd откладываем влево от плоскости, а отрезок dxd’ – вверх от плоскости Н.
Положения точек А и D, получены на пересечении перпендикуляров, проведенных через точки а и d к плоскости Ни через точки а’ и d’ к плоскости V.
Точка В лежит в плоскости V, это следует из того, что проекция b лежит на оси х (ордината равна 0) следовательно на рис б, точка b совпадает с bх . Отрезок bхb’ соответствующий отрицательному значению аппликаты откладываем вниз от плоскости Н. Положение самой точки В совпадает с положением ее фронтальной проекции b’.
Точка С располагается на плоскости Н, это следует из того, что проекция с’ лежит (рис. а) на оси х (аппликата точки С равна 0) Поэтому и на рис. б схс’.
Так как для точки С ордината положительна, то соответствующей этой ординате отрезок схс откладывается вправо от плоскости V, положение самой точки совпадает с положением ее горизонтальной проекции с.
Задача № 7.Изобразить наглядно положения точек А,B,C,D и E, заданных своими проекциями на рисунке.
Задача № 8*.Построить проекции точек А и В по их координатам. Построить проекцию точки С, расположенной симметрично точке А относительно фронтальной плоскостей проекций. Изобразить наглядно положения этих точек относительно плоскостей V и Н.
| координаты точка | x | y |
| A | 13,5 | |
| B | 6,5 | -20 |
Решение.Намечаем ось х (рис.а) и на ней точку ах . Так кА точка А положительна, расположена в первой четверти (аппликата и ордината положительны), то проекция а’ находится над осью х на расстоянии 13,5.
Для построения точки В сначала задаемся (на оси х) произвольно точкой bх и откладываем вниз отрезок bх b равный значению ординаты 6,5 и отрезок bх b’, соответствующий отрицательному значению аппликаты (-20). Точка В находится в первой четверти.
Точка С должна быть расположена симметрично точке А относительно плоскости V. Следовательно ордината точки С равна -13,5, а аппликата равно 20. Точка сх совпадает с точкой ах, с’ – с а’, а горизонтальная проекция с находится над осью х на расстоянии 13,5.
Задача № 9.Построить проекции точек А, В, С по их координатам. Построить проекцию точки D ,расположенной симметрично точке С относительно оси х. Изобразить наглядно положения этих точек относительно плоскостей V и Н.
| координаты точка | x | y |
| A | -25 | |
| B | -20 | |
| С | -30 | -20 |
| х |
Задача № 10. Построить недостающие проекции точек А, В, С, D и их наглядное изображение в системе трех плоскостей проекций.
Тема 1.3. Проекции прямой линии. Взаимное положение прямых в пространстве.
| Задача № 11. По заданным фронтальной а2 и профильной а3 проекциям прямой построить горизонтальную проекцию а1 , прямой а |  |
 | Задача № 12. По фронтальному N2 и профильному T3 следам прямой а построить её проекции. Определить через какие октанты она проходит. |
| Задача № 13. По горизонтальному M1 и профильному T3 следам прямой а построить её проекции. Определить через какие октанты она проходит. | 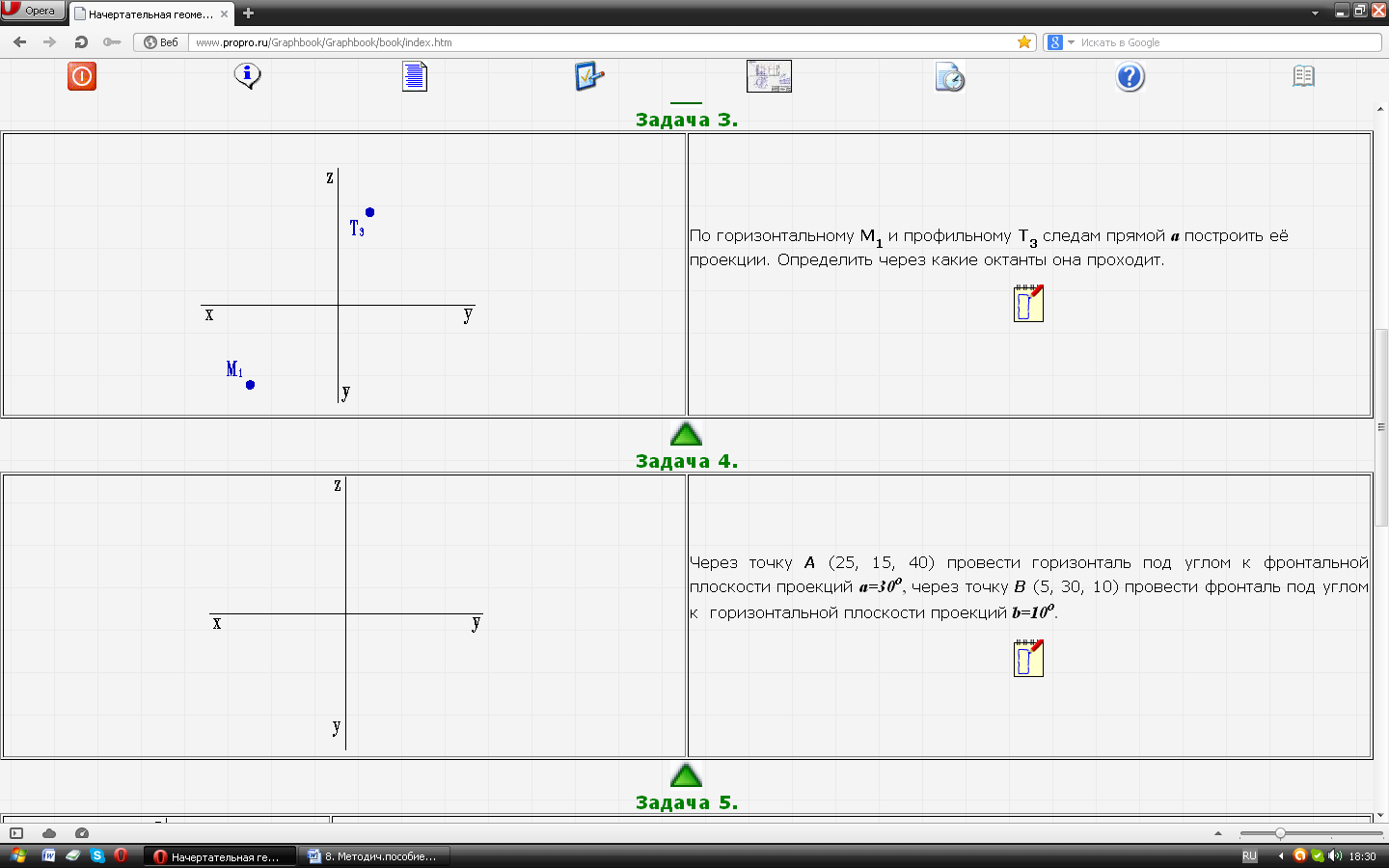 |
| Задача № 14. Через точку А (25, 15, 40) провести горизонталь под углом к фронтальной плоскости проекций a=30 o , через точку В (5, 30, 10) провести фронталь под углом к горизонтальной плоскости проекций b=10 o . | |
 | |
| Задача № 15. Построить три проекции отрезка АВ прямой линии п по заданным координатам ее концов А(30,10,10) , В(10,25,40). Построить проекции точки С, делящей отрезок в отношении АС:СВ=1:2. | |
 | |
| Задача № 16. Построить следы прямой линии заданной отрезком | 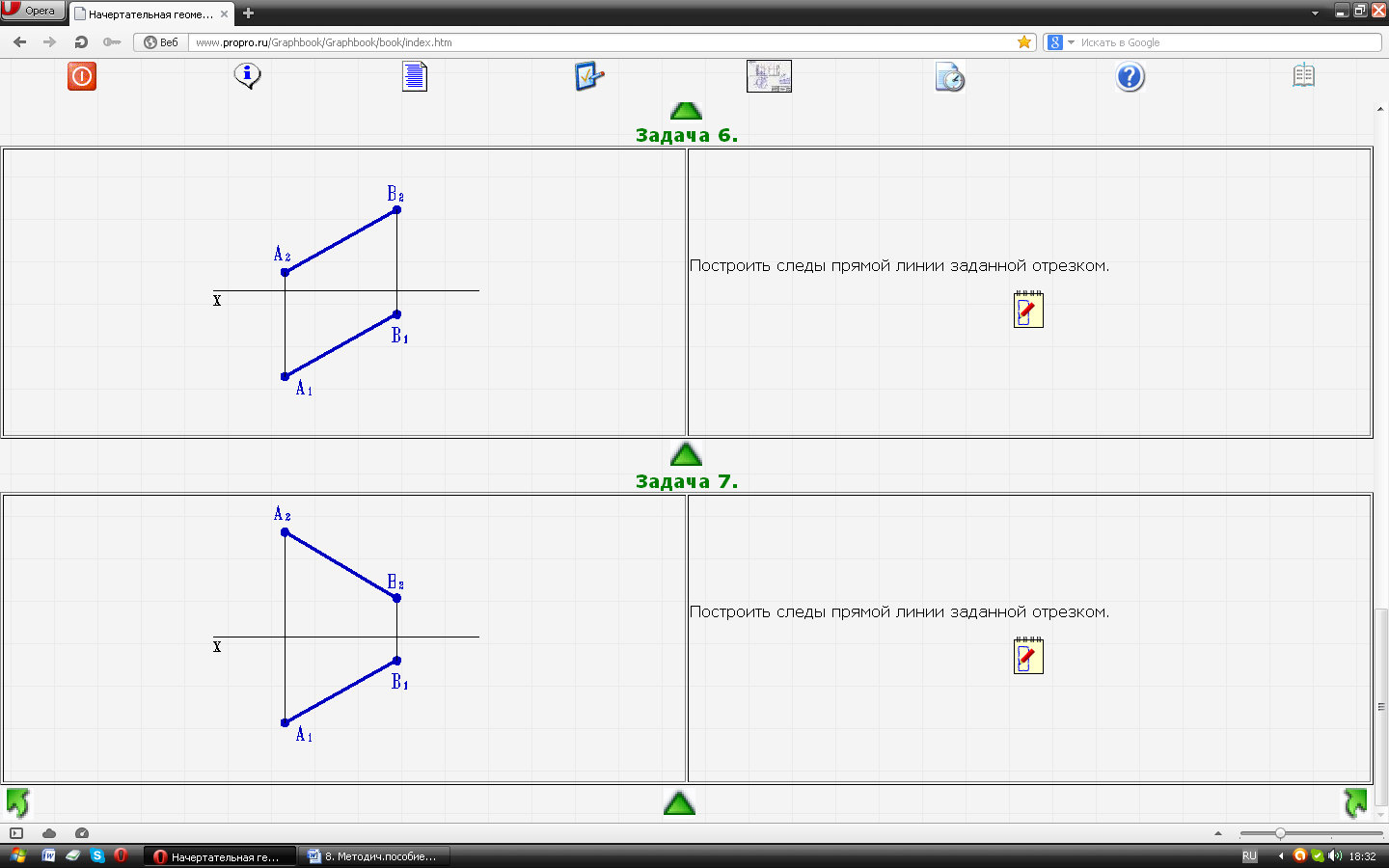 |
 | Задача № 17. Построить следы прямой линии заданной отрезком |
| Взаимное расположение точки и прямой | |
| Задача № 18.Определить какая из предложенных на проекциях точек принадлежит прямой m. |  |
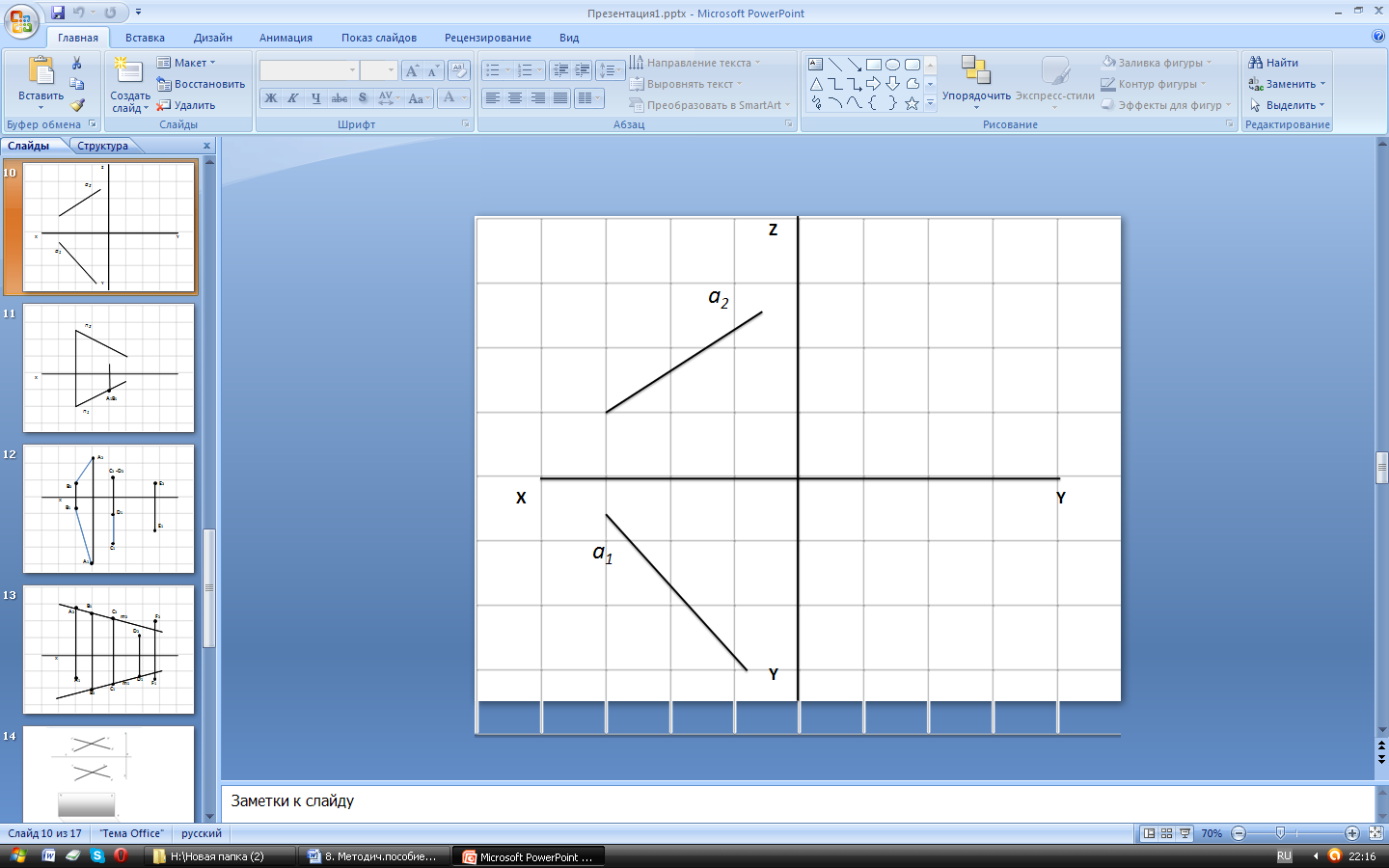 | Задача № 19.Построить проекции точки А равноотстоящей от плоскостей П1 и П2 и принадлежащей прямой а заданной на эпюре. |
| Задача № 20.Построить недостающие проекции точек А и В, если известно, что точка А лежит на прямой п, а В на 10 мм выше точки А. |  |
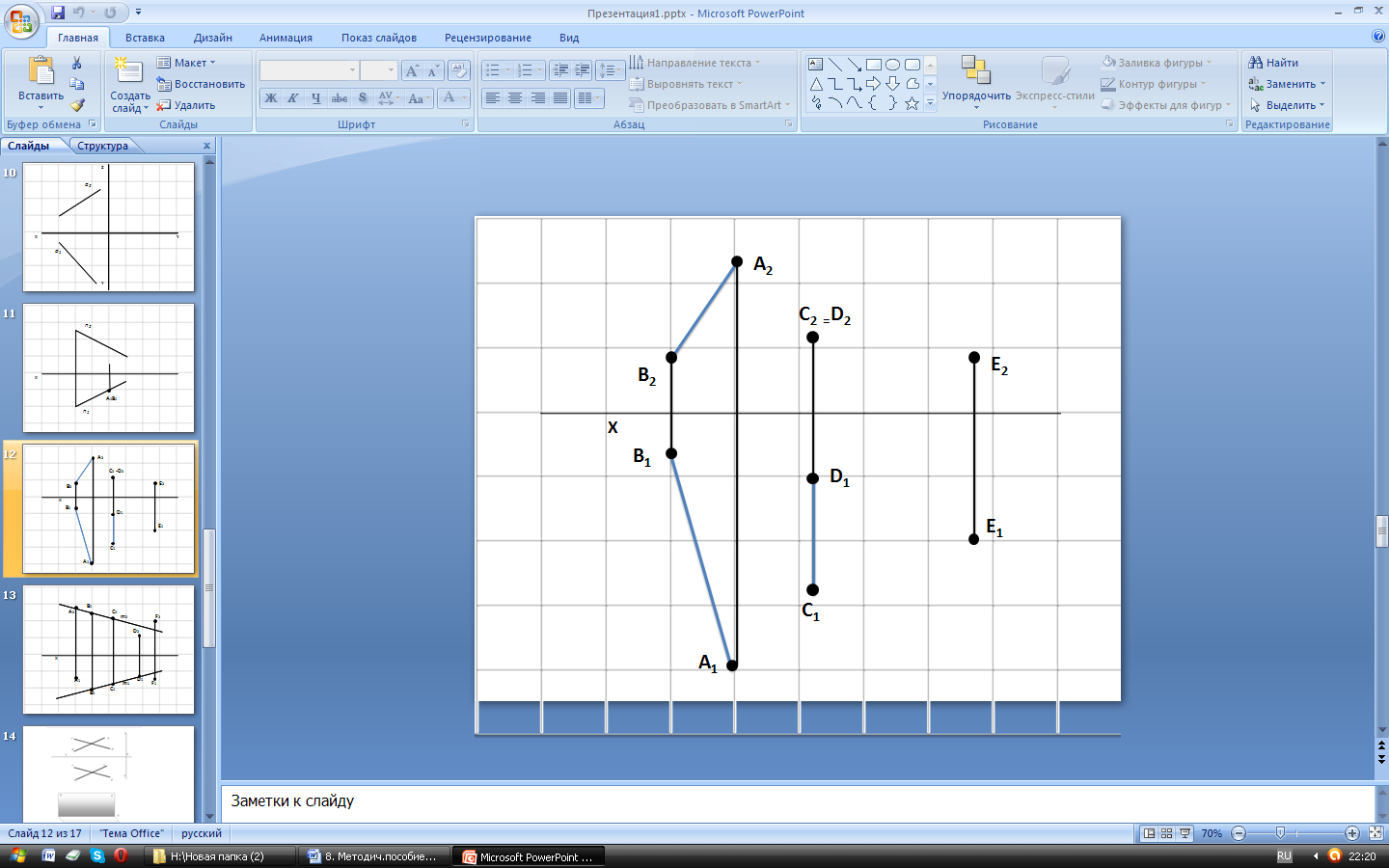 | Взаимное расположение прямых Задача № 21.Через точку Е провести прямую, пересекающую прямые АВ и СD. |
Тема 1.4. Плоскость.
| Задача № 22.По координатам трех точек А(45,30,10), B(30,10,45) и С(5,25,5) построить проекции плоскости и её следы. | 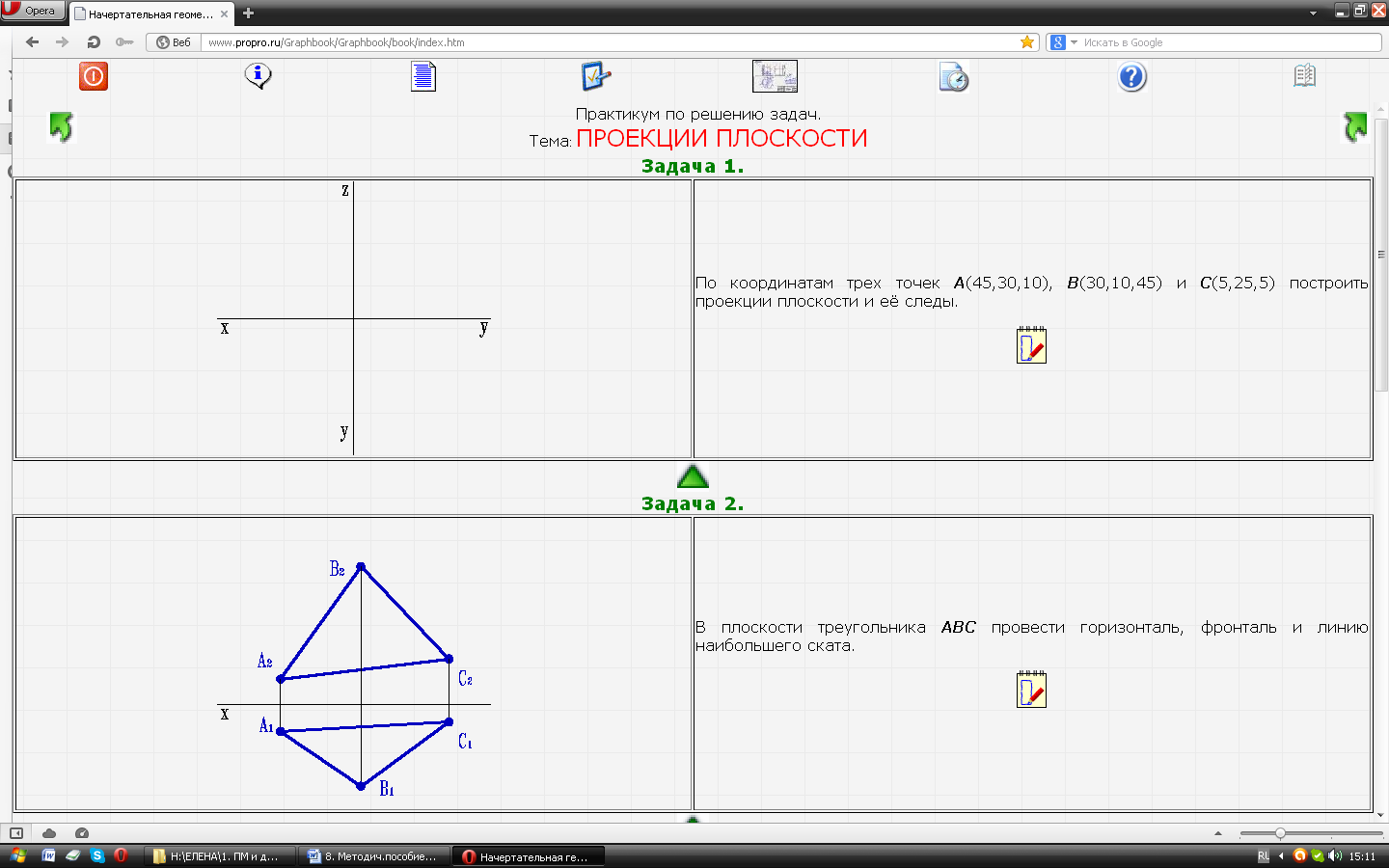 |
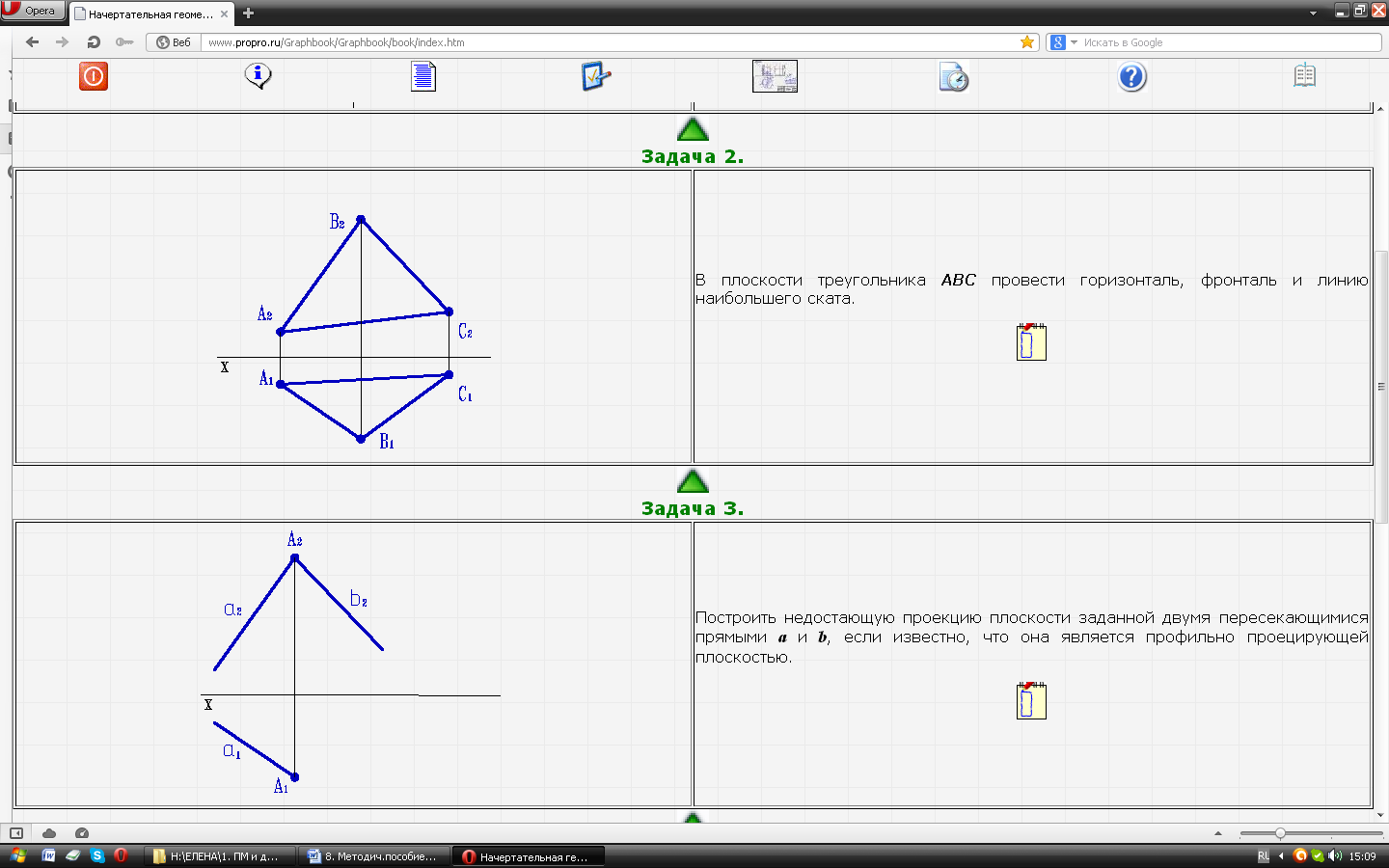 | Задача № 23. В плоскости треугольника АВС провести горизонталь, фронталь и линию наибольшего ската. |
| Задача № 24.Построить недостающую проекцию плоскости заданной двумя пересекающимися прямыми a и b, если известно, что она является профильно проецирующей плоскостью. |  |
Тема 1.5. Задание точки и прямой в плоскости.
Прямая и точка в плоскости. Главные линии плоскости. Пересечение прямой и плоскости. Определение видимости на чертеже.
| Задача № 25 Построить недостающую проекцию точки D принадлежащей плоскости АВС. | 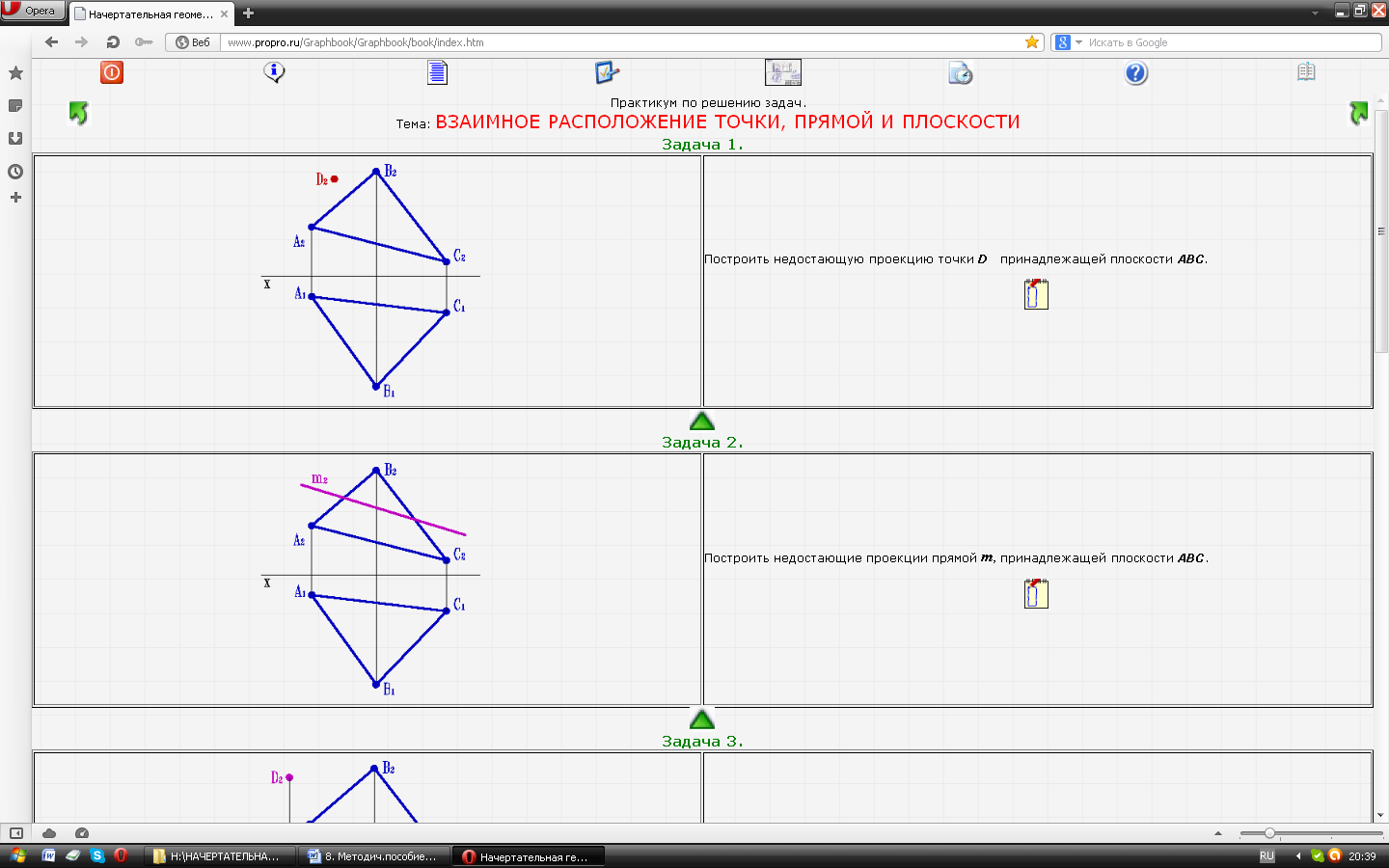 |
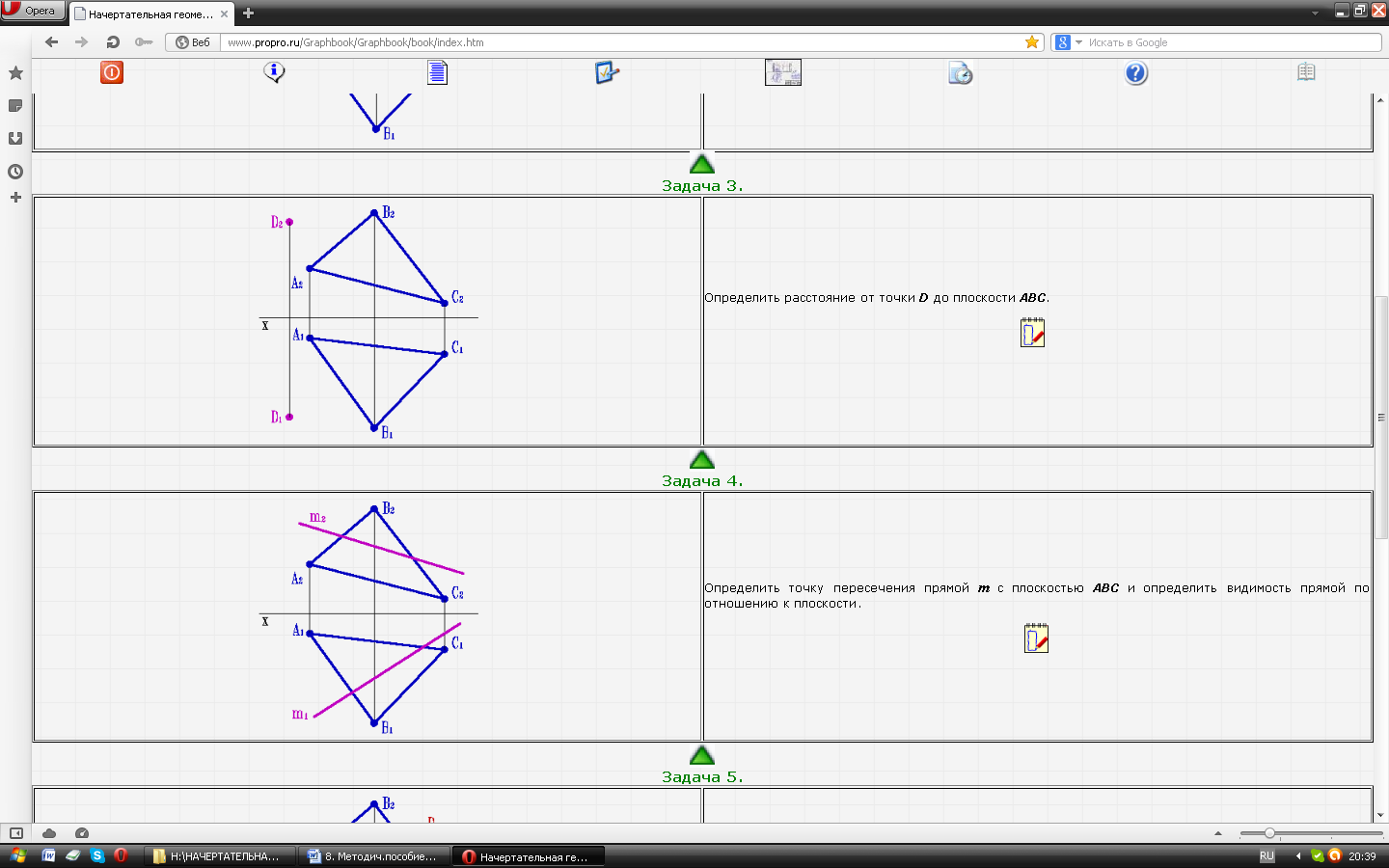 | Задача № 26. Определить расстояние от точки D до плоскости АВС |
 | Задача № 27. Построить недостающие проекции прямой m, принадлежащей плоскости АВС.. |
| Задача № 28 Определить точку пересечения прямой m с плоскостью АВС и определить видимость прямой по отношению к плоскости. |  |
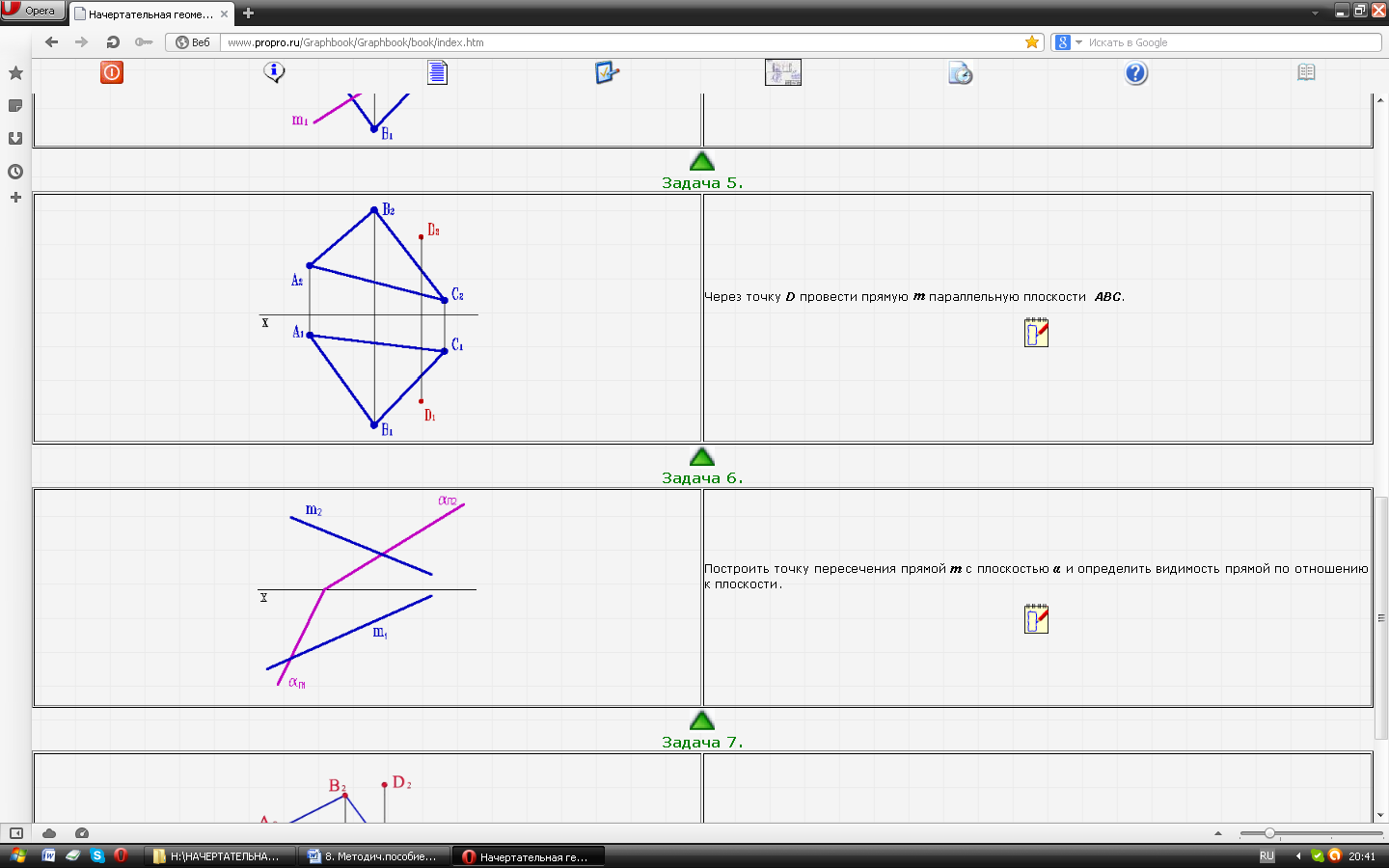 | Задача № 29. Через точку D провести прямую параллельную плоскости АВС. |
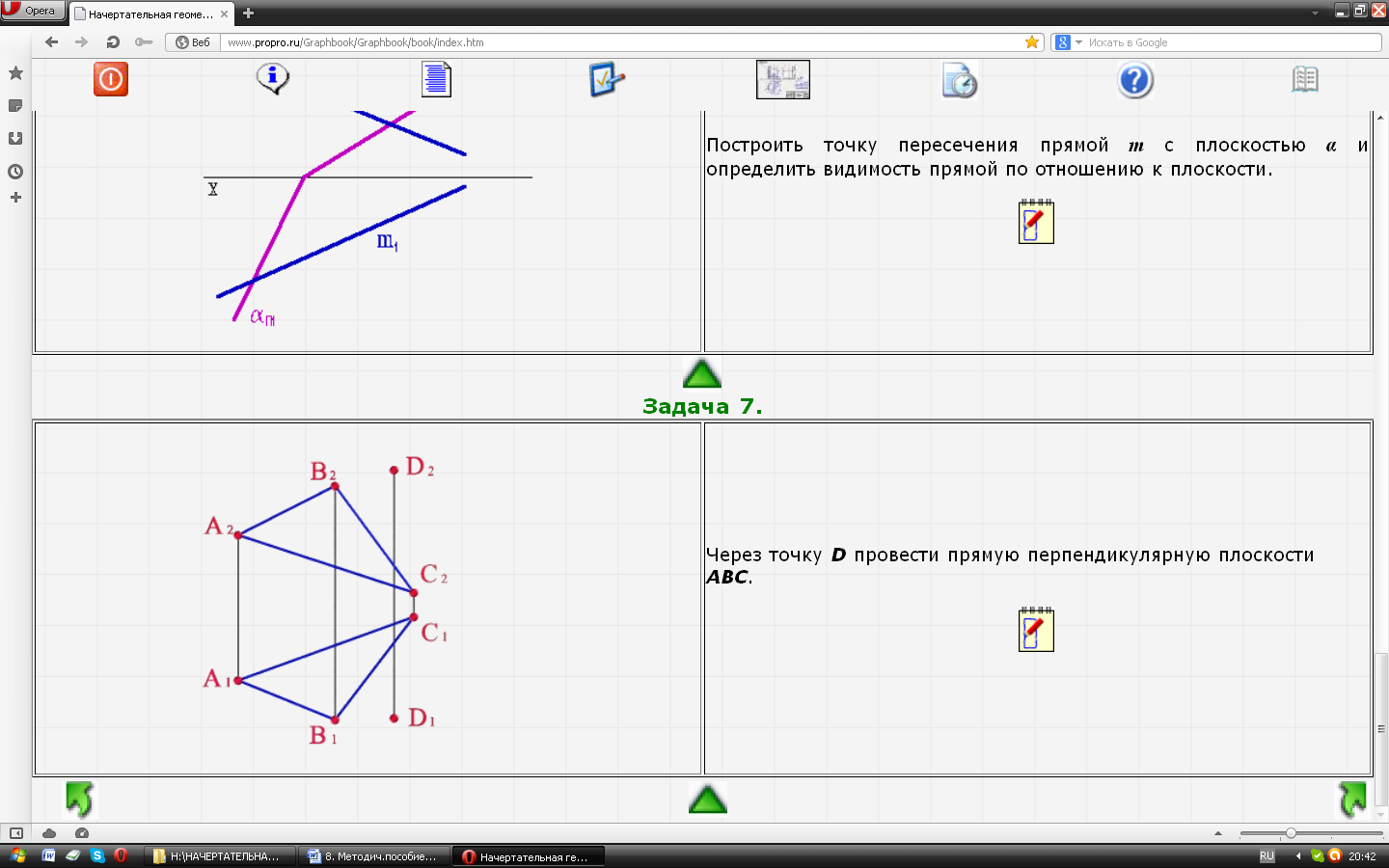 | Задача № 30. Через точку D провести прямую перпендикулярную плоскости АВС. |
| Тема 1.6.Взаимное положение плоскостей. | |
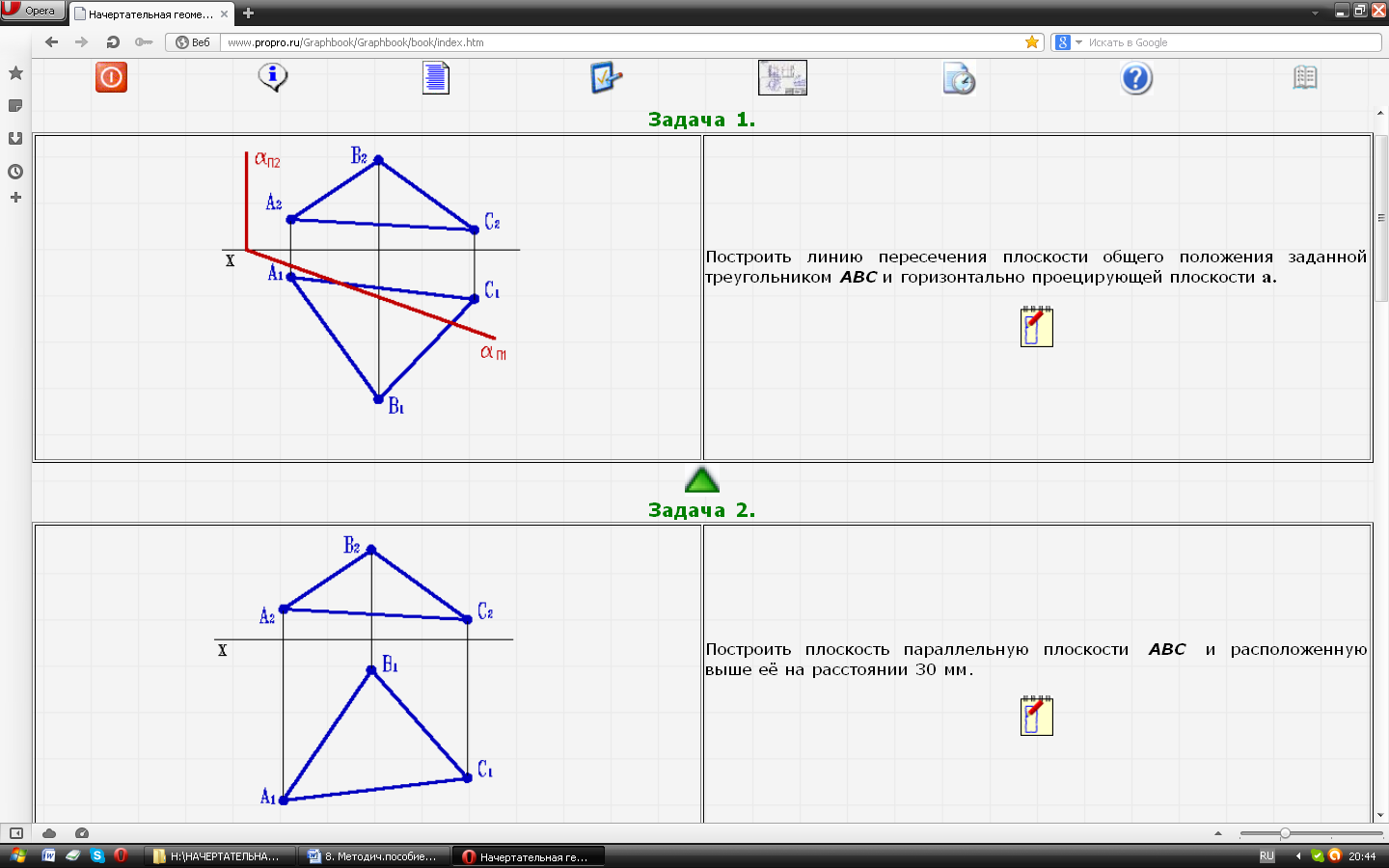 | Задача № 31. Построить плоскость параллельную плоскости АВС и расположенную выше её на расстоянии 30 мм. |
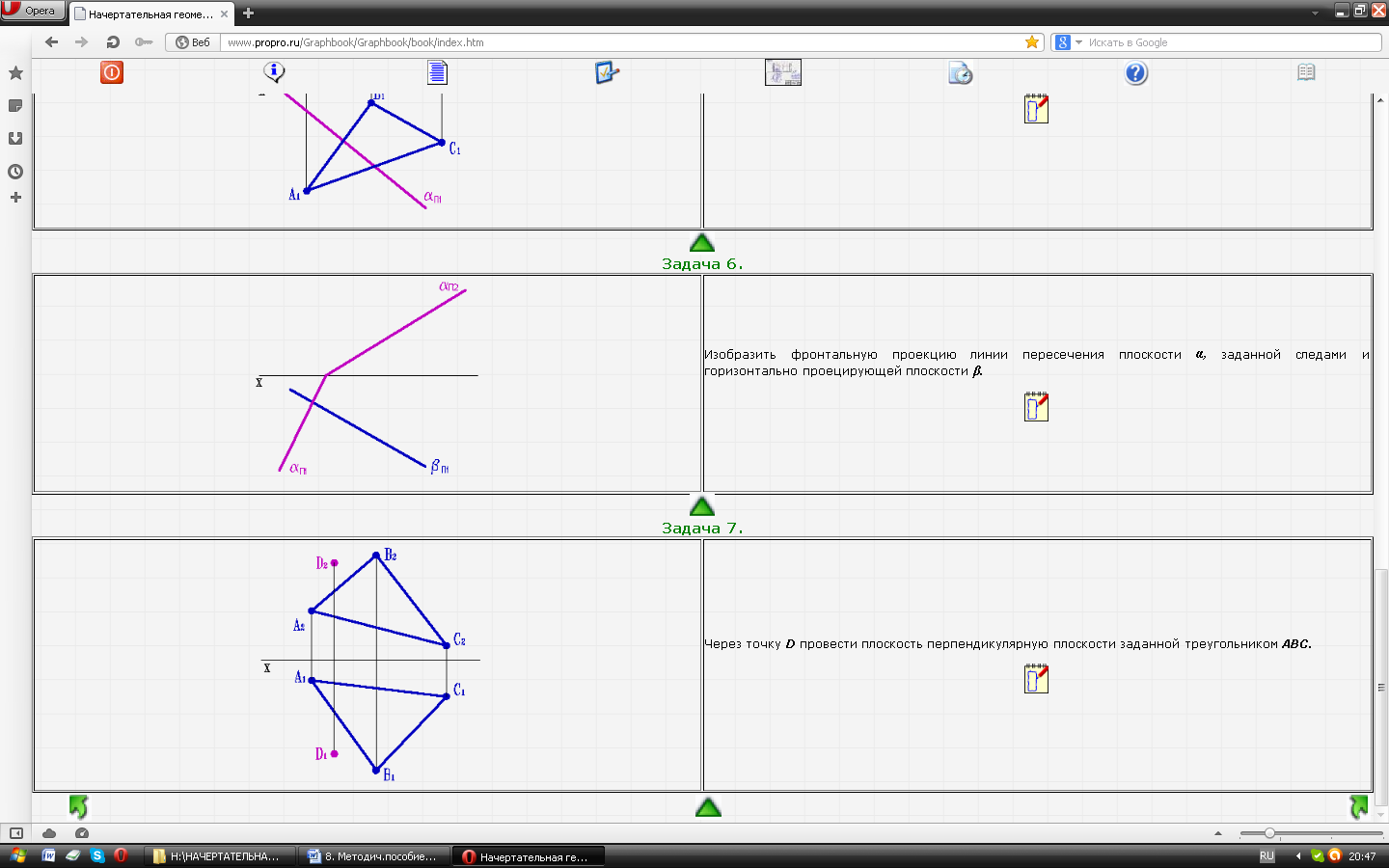 | Задача № 32. Через точку D провести плоскость перпендикулярную плоскости заданной треугольником АВС. |
| Задача № 33. Построить линию пересечения плоскости АВС и плоскости заданной двумя параллельными прямыми п и т. Определить видимость. | 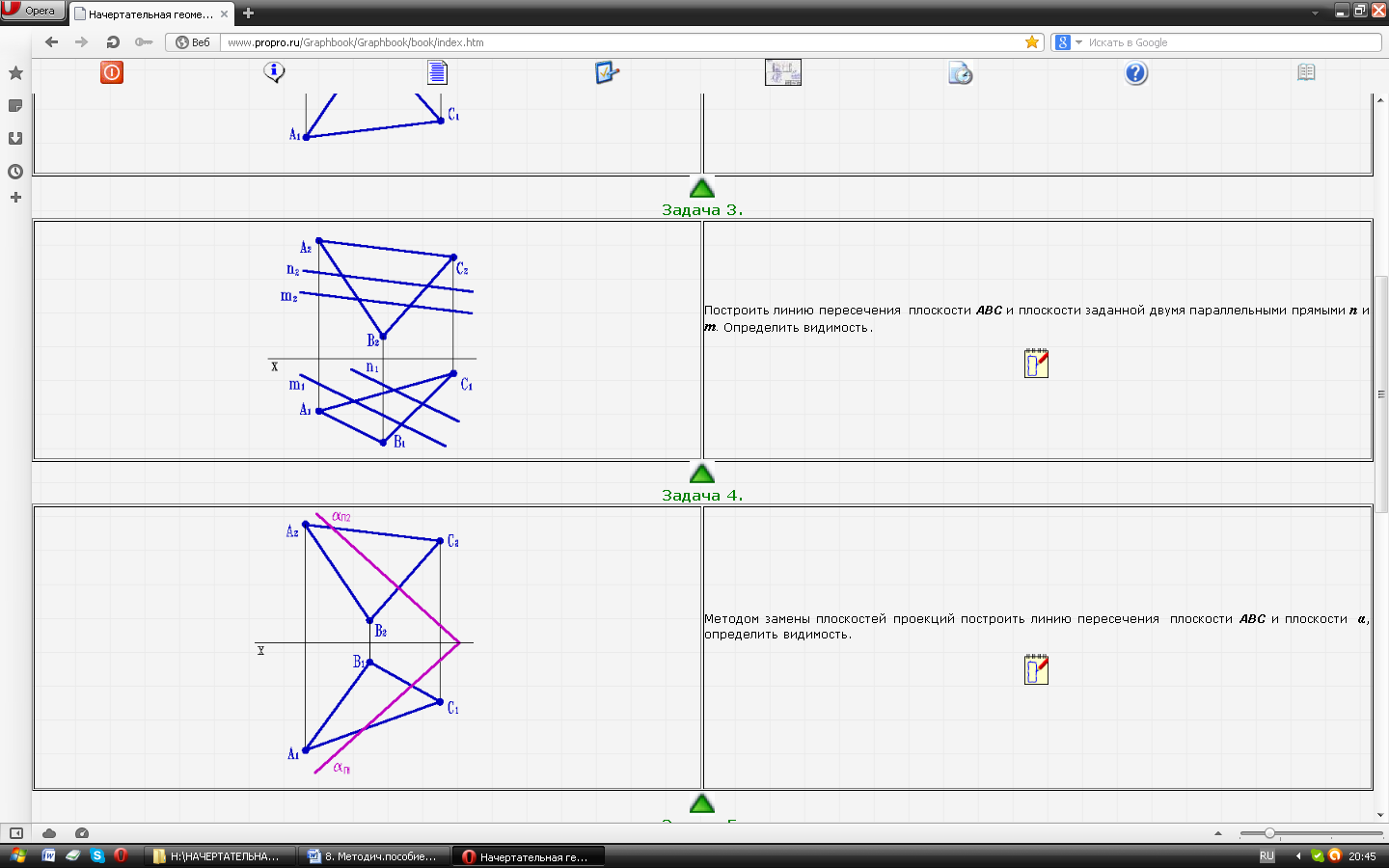 |
Тема 1.7.Способы преобразования проекционного чертежа.
Источник