Построить линию пересечения поверхностей способом вспомогательных концентрических сфер

Построение линии пересечения конусов методом концентрических сфер

На рисунке ниже изображены два конуса вращения. Их оси i₁ и i₂, пересекаясь в точке O, образуют плоскость α(i₁∩i₂), которая параллельна фронтальной плоскости проекций π₂.

Для построения линии пересечения конусов, показанных на рисунке, целесообразно использовать метод концентрических сфер. Применение данного метода возможно в результате выполнения следующих условий:

• пересекаются поверхности вращения (в частности, конус с конусом, конус с тором или цилиндром и т.д.);
• оси поверхностей, пересекаясь между собой, образуют плоскость, которая параллельна одной из плоскостей проекций (в рассматриваемом примере пл. α(i₁∩i₂)∥π₂).

Алгоритм построения линии пересечения

Построение линии пересечения начинают с нахождения характерных точек, которые определяют ее границы и видимость относительно плоскостей проекций.

Определение характерных точек

Плоскость α, образованная пересекающимися осями i₁ и i₂, является общей плоскостью симметрии двух конусов. На рисунке показан ее горизонтальный след h_0α. Пересечение пл. α с конусами происходит по образующим S₂A, S₂B и S₁C, S₁D. Данные образующие ещё называют очерковыми, так как они очерчивают границы поверхностей (на фронтальной проекции).

Точки F’’, E’’, G’’, K’’, в которых пресекаются прямые S’’₂A’’, S’’₂B’’ с прямыми S’’₁C’’ и S’’₁D’’, определяют границы линии пересечения конусов в её проекции на плоскость π₂. Для нахождения F’, E’, G’ и K’ проводят линии связи из F’’, E’’, G’’, K’’ до горизонтального следа h_0α.

Определение промежуточных точек

Воспользуемся методом концентрических сфер для нахождения множества промежуточных точек линии пересечения. Центром, из которого проводятся вспомогательные сферы, является точка O пересечения осей i₁ и i₂ рассматриваемых конусов.

Радиус R_max наибольшей сферы, применяемой в построениях, равен длине отрезка O’’G’’ – расстоянию от точки O до наиболее удаленной от нее точки G пересечения очерковых образующих.

Сфера минимального радиуса R_min – это сфера, вписанная в один из конусов и пересекающая другой. На рисунке ниже R_min= O’’H’’, где O’’H’’⊥ S’’₂B’’.

Рассмотрим построение точек 1, 2, 3 и 4. Сфера радиусом R_min пересекается с конусом, в которой она вписана, по окружности. Данная окружность проецируется на фронтальную плоскость проекций в виде отрезка P’’H’’. Кроме того, сфера радиусом R_min пересекается со вторым конусом по двум окружностям, диаметры которых соответственно равны длинам отрезков M’’N’’ и T’’L’’. Таким образом, на поверхности сферы лежат три окружности, которые пересекаются в общих для двух конусов точках 1, 2, 3 и 4.

Фронтальные проекции 1’’, 2’’, 3’’, 4’’ находятся на пересечении отрезков M’’N’’, T’’L’’ с P’’H’’. Для нахождения горизонтальных проекций 1’, 2’, 3’, 4’ точек 1, 2, 3, 4 на плоскости проекций π₁ из центра O’ проводим две окружности с диаметрами M’’N’’ и T’’L’’. Учитывая принадлежность точек соответствующим окружностям, по линиям связи определяем их горизонтальные проекции, как это показано на рисунке выше.

С помощью вспомогательной сферы радиусом R_var, где R_min ≤ R_var ≤ R_max, найдены точки 5 и 6. Как видно из построений, они находятся на пересечении двух окружностей, которые проецируются на фронтальную плоскость в виде отрезков W’’U’’ и Q’’V’’.

В описываемом способе решения каждая сфера играет роль посредника, содержащего на своей поверхности кривые (окружности), принадлежащие пересекающимся конусам. Действуя в соответствии с приведенным выше алгоритмом, необходимо найти такое количество точек, которое позволит определить геометрическую форму линии пересечения на каждой из проекций.

Найденные точки соединяем плавными кривыми с учетом их видимости. Как видно на рисунке, в результате пересечения конусов образовались две замкнутые линии. Они показаны красным цветом.

Источник

Способ концентрических сфер

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ.

СПОСОБ ВСПОМОГАТЕЛЬНЫХ ЭКСЦЕНТРИЧЕСКИХ СФЕР.

Способ концентрических сфер.

Рассмотрим построение линии пересечения двух поверхностей, когда в качестве поверхности-посредника используется сфера. При этом возможны два случая применения сфер:

1) вспомогательные сферы могут быть проведены из одного общего для всех сфер центра. В этом случае говорят о способе концентрических сфер,

2) вспомогательные сферы проводятся из разных центров. Этот способ называют способом эксцентрических сфер.

Предварительно скажем несколько слов о пересечении соосных поверхностей, т.е. поверхностей, имеющих общую ось вращения.

Пусть заданы две образующие линии (два главных меридиана) -прямая l и дуга окружности m (рисунок 12-1). При вращении их вокруг оси i будут описаны соответственно цилиндрическая и торовая поверхности. Каждая точка заданных линий при вращении вокруг оси i описывает в пространстве окружность, плоскость которой перпендикулярна оси вращения.

Полученные поверхности пересекаются, причем линий пересечения будет столько, сколько точек пересечения имеют сами образующие линии (меридианы). Поскольку в нашем случае они пересекаются в двух точках, будет и две линии пересечения поверхностей, которые представляют собой окружности (параллели).

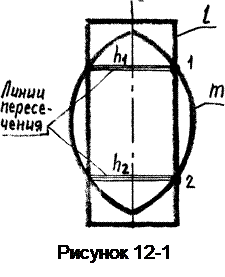
В частном случае одной из соосных поверхностей может быть сфера, если центр дуги окружности m находится на оси вращения i.

Таким образом, если центр сферы находится на оси некоторой поверхности вращения, то эта поверхность пересекается со сферой по окружностям. Это свойство и положено в основу способа вспомогательных сфер.

Способ концентрических сфер следует применять в случаях, когда соблюдаются следующие три условия:

· пересекаются поверхности вращения или поверхности, содержащие семейства окружностей, по которым их могут пересекать концентрические сферы;

· оси поверхностей вращения пересекаются;

· поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций. Если же она не параллельна ни одной из плоскостей проекций, то необходимо произвести преобразование чертежа для достижения необходимых условий решения.

Пример 1. Построить линию пересечения конуса вращения с цилиндром вращения (рисунок 12-2).

Сначала определим некоторые опорные точки. Так как поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций, то пересечение их контурных образующих в точках А и В определяет высшую и низшую точки линии пересечения.

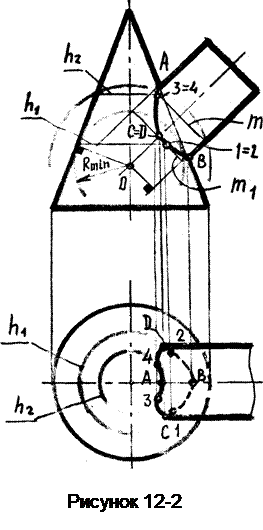
Центр сфер 0 выбирают в месте пересечения осей цилиндра и конуса, т.к. только в этом случае сферы будут соосны с обеими поверхностями.

Определим радиус минимальной Rmin и максимальной Rmax сфер, которые будем использовать при решении задачи. Rmax определяется расстоянием от точки 0 до самой удаленной опорной точки.

Для определения Rmin необходимо из центра 0 опустить перпендикуляры на очерковые образующие поверхностей из центра 0 опустить перпендикуляры на очерковые образующие поверхностей. Больший из них принимается в качестве Rmin, т.к. сфера такого радиуса будет касаться одной и пересекать вторую поверхность, что дает возможность найти общие для обеих поверхностей точки — точки линии пересечения. При радиусе сферы меньшем Rmin она не будет иметь общих точек с одной из поверхностей; построения теряют смысл.

Для построения случайных точек проводим сферы радиуса Rmin

· каждая поверхность содержит семейство окружностей, по которым её могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Пример 2. Построить линию пересечения конуса вращения со сферой (рисунок12-3).

Плоскостью симметрии данных поверхностей является фронтальная плоскость, поэтому можно применить способ вспомогательных сфер. Каких?

Задачу можно решить как способом концентрических сфер, так и эксцентрических. Решим её вторым способом.

Центр сфер можно брать в любой точке оси конуса вращения. На рисунке 12-3 проведены три сферы радиусов RI, R2, R3. Каждая из этих сфер пересекается с каждой из данных поверхностей по окружности, точки пересечения которых будут точками линии пересечения.

На виде сверху точки находим с помощью параллелей конуса h¹,h²,h³.

Пример 2. Построить линию пересечения конуса вращения с тором (рисунок 12-4).

Эту задачу можно решить только способом эксцентрических сфер.

Обе поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций, в которой расположены ось конуса и линия центров тора.

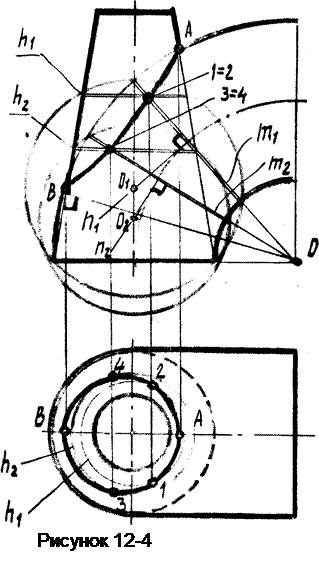
Как и во всех задачах на пересечение поверхностей, вначале определяем опорные точки. Самая верхняя и правая — т. А, расположенная на пересечении контурных линий. Чтобы найти нижнюю и левую т. В (точку касания контурных линий конуса и тора), необходимо из т. О опустить перпендикуляр на контурную образующую конуса; их пересечение определяет т.В.

Для построения дополнительных точек выделим одну окружность –m принадлежащую поверхности тора.

Центры всех сфер, которые будут пересекаться с тором по этой окружности, будут лежать на прямой n1 данной окружности C1 перпендикулярно к её плоскости. Эта прямая пересечёт ось конуса (т.к. они лежат в одной плоскости) в т. 01. Эта точка будет центром сферы, которая пересечёт поверхность конуса по окружности h1. Окружности m1 и h1 пересекаются в точках 1 и 2, которые будут принадлежать линии пересечения.

Для нахождения дополнительных точек нужно взять новую окружность на поверхности тора и все действия повторить.

На виде сверху точки линии пересечения находят при помощи параллелей конуса h.

Источник

Алгоритм решения

Способ вспомогательных сфер

При построении линии пересечения двух поверхностей способом

вспомогательных сфер возможны два случая:

-способ концентрических сфер– сферы проведены из одного, общего для всех сфер центра;

— способ эксцентрических сфер– сферы проведены из разных центров.

Способ концентрических сфер − сфер с постоянным центром.

Этот способ применяют при выполнении следующих условий:

а) пересекающиеся поверхности должны быть поверхностями вращения;

б) оси этих поверхностей должны пересекаться; точку их пересечения принимают за центр вспомогательных сфер;

в)плоскость симметрии поверхностей должна быть параллельна какой-либо плоскости проекций.

1. Обозначается плоскость симметрии.

2. Определяется центр вспомогательных секущих сфер. Он находится в точке пересечения осей данных поверхностей.

3. Определяются радиусы минимальной и максимальной вспомогательных сфер. За Rmin принимается величина большей нормали. Rmax равно расстоянию от центра сфер до наиболее удаленной от него опорной точки.

4. Проводится сфера минимального радиуса. Она будет касаться одной поверхности по окружности и пересекать вторую тоже по окружности. Точки пересечения этих окружностей будут являться точками искомой линии пересечения.

5. Для определения промежуточных точек линии пересечения из центра проводится семейство секущих сфер, величины радиусов которых изменяются в пределах от Rmin до Rmax (Rmin≤R≤Rmax).

6. Одноименные проекции точек соединяются плавной кривой линией.

7. Определяется видимость.

Задача 3. Построить проекции линии пересечения поверхностей прямого кругового конуса α с поверхностью прямого кругового цилиндра β.

Решение:

Шаг 1. Оси поверхностей вращения пересекаются в точке О=i Çi 2 . Плоскость симметрии Δ||П₂, следовательно задача решается способом концентрических сфер (рис.24).

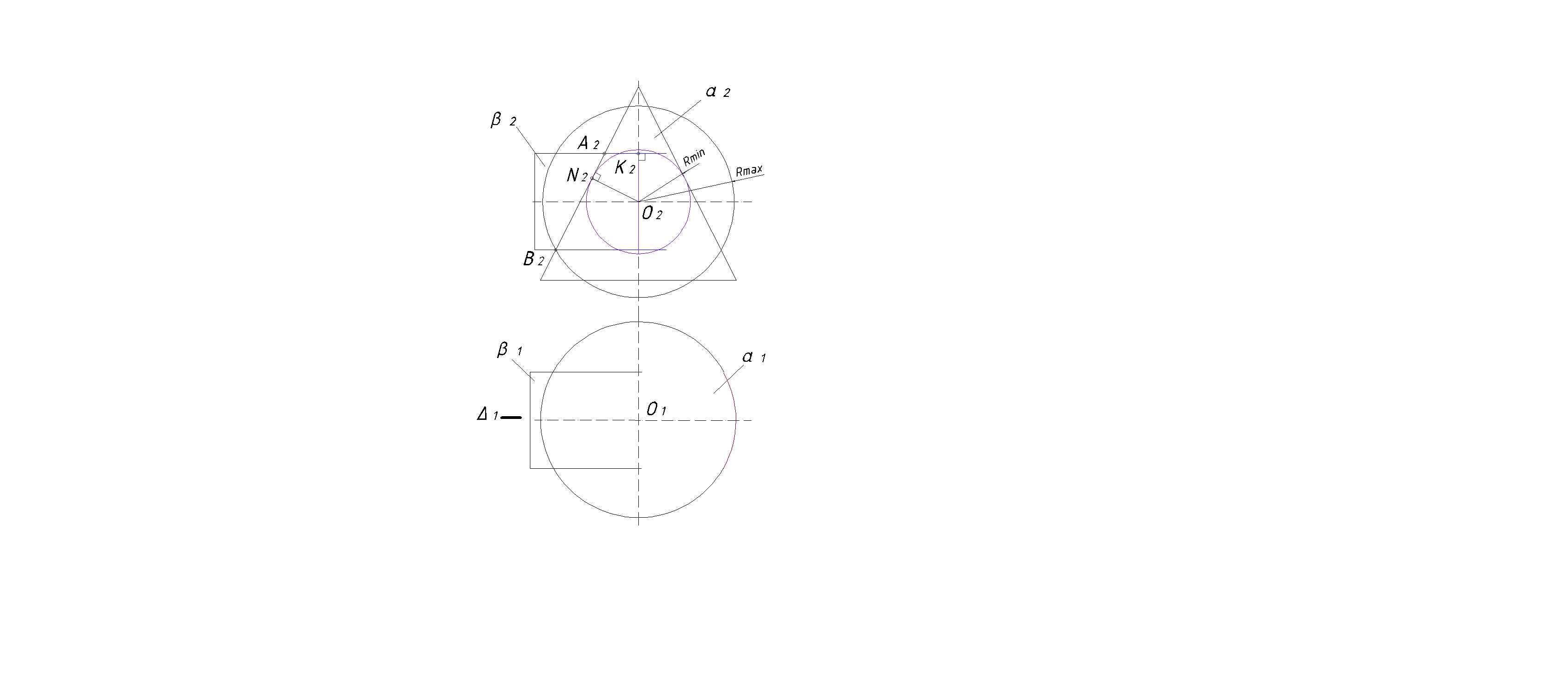Рис. 24

Шаг 2. За центр сфер принимается точка пересечения осей заданных поверхностей. Отметим проекции точки О(О₁,О₂) пересечения осей заданных поверхностей и принимаем их за проекции общего центра всех секущих сфер.

Определим радиусы максимальной и минимальной сфер. Радиус максимальной сферы равен расстоянию от центра сфер до наиболее удаленной точки пересечения линий очерков поверхностей (Rmax=.О₂B₂).

Радиус минимальной сферы определяется из условия касания минимальной сферы одной поверхности (вписывается в поверхность) и пересечения второй. Для определения минимального радиуса Rmin секущей сферы из точки О₂ проводим перпендикуляры на очерковые образующие поверхностей. Больший из этих перпендикуляров (перпендикуляр О₂N₂ на образующую конусаα принимаем за Rmin (Rmin= О₂N₂).

Для построения промежуточных точек линий пересечения обе поверхности пересекаем концентрическими сферами, радиусы которых находятся в диапазоне Rmin

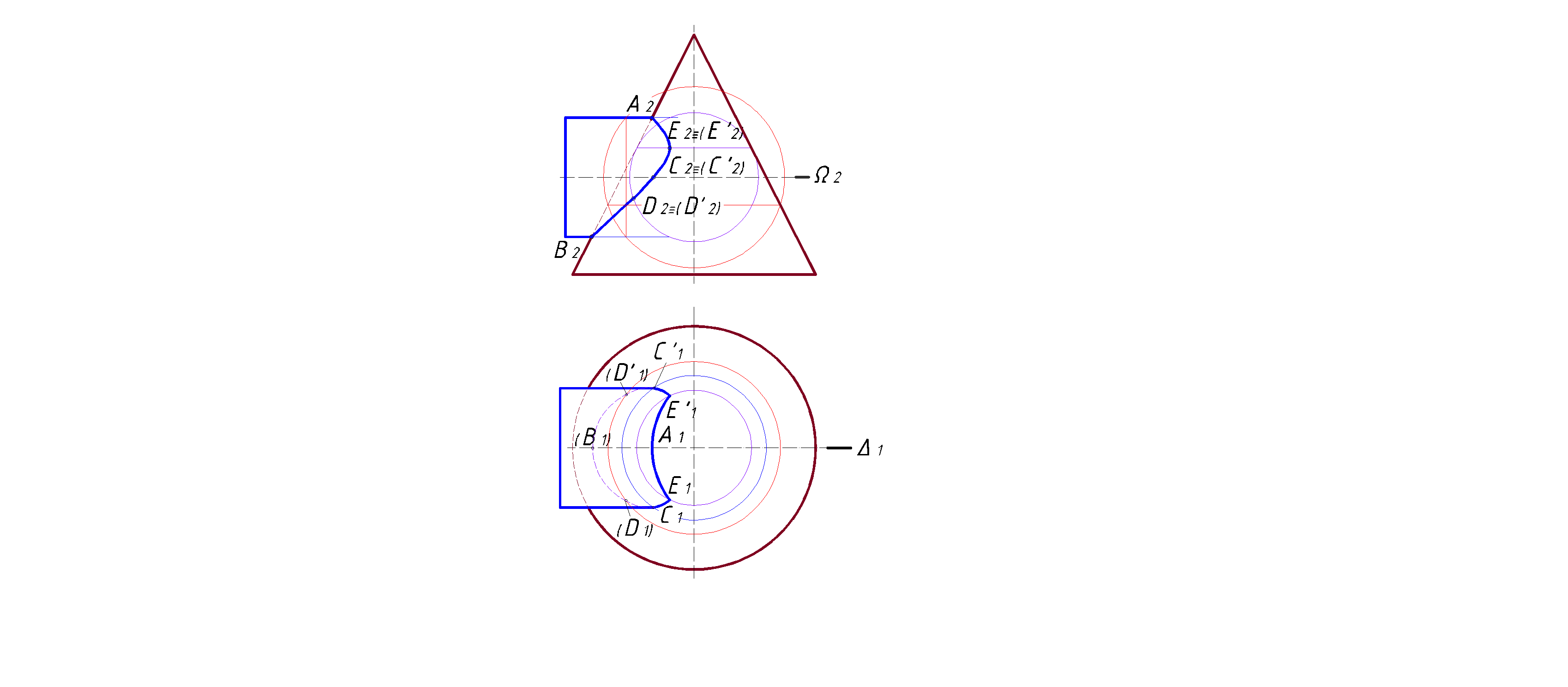Рис.27

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник