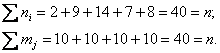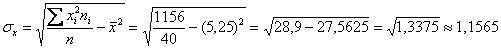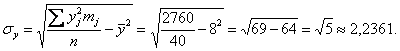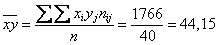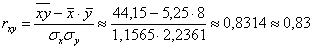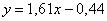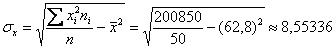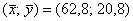20. Уравнение линейной регрессии
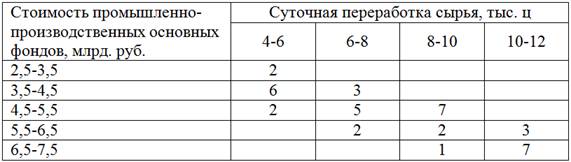
На предыдущем уроке мы уже узнали, что такое линейная регрессия и научились находить её уравнение для несгруппированных данных (это когда даны две строчки или два столбца чисел). И сейчас тема получает продолжение – в данной статье я расскажу вам о том, как вычислить линейный коэффициент корреляции и как найти уравнение линейной регрессии в случае комбинационной группировки. Это когда в условии дана комбинационная таблица:
Имеются выборочные данные по 40 предприятиям региона:
1) Определить признак-фактор 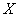
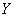
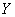
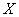
2) Вычислить линейный коэффициент корреляции и детерминации, сделать выводы.
3) Найти уравнение линейной регрессии 
Все термины и понятия вам уже знакомы! А если нет, то будут ссылки по ходу решения и, конечно же, видео – как это всё быстро подсчитать и нарисовать в Экселе + Калькулятор (сразу для особо страждущих).
1) Прежде всего в подобных задачах нам нужно обосновать причинно-следственную связь между признаками (если это не сделано в условии). Очевидно, что чем больше стоимость основных фондов, тем крупнее предприятие и тем больше сырья оно способно переработать. Однако это не является непреложным правилом, ибо любое, самое крупное предприятие может неэффективно работать или даже простаивать. Тем не менее, общая тенденция состоит в том, что при увеличении стоимости фондов предприятий их средняя суточная переработка растёт. Такая нежёсткая зависимость называется… Правильно! Я приду к вам в вещих снах – будете вздрагивать и просыпаться от этой фразы 🙂
Таким образом, мы предполагаем наличие прямой корреляционной зависимости суточной переработки сырья (признак-результат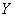
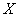
Частоты комбинационной таблицы располагаются преимущественно по диагонали – от левого верхнего до правого нижнего угла, что подтверждает прямое направление зависимости («чем больше, тем больше»).
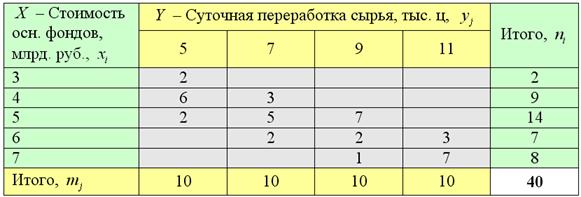
Теперь определим форму зависимости (линейная, квадратичная, экспоненциальная или какая-то другая). Простейший способ – графический, построили корреляционное поле и посмотрели. Для этого нужно немного модифицировать исходную таблицу, а именно перейти от интервальных вариационных рядов (левый столбец и 2-я сверху строка) к дискретным, выбрав в качестве вариант 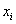
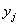
Заодно подсчитаем суммы частот по серым строкам (правый столбец) и суммы частот по серым столбцам (нижняя строка), не забыв убедиться в том, что итоговые суммы равны объёму выборки 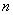
Довольно часто значения 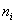
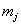
Обратите внимание, что значения 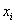
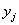
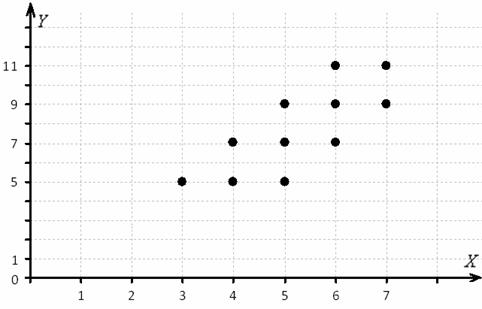
Ранее мы строили эмпирические линии регрессии – это простейший способ изобразить форму корреляционной зависимости. Однако гораздо удобнее привлечь на помощь функции. Анализируя чертёж, приходим к выводу, что эмпирические точки 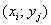
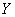
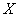
Дальнейшие действия состоят в том, чтобы отыскать уравнение линейной регрессии 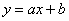
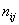
2) Коэффициент корреляции вычислим по знакомой формуле 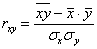
Лично я привык в первую очередь находить средние 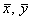
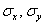
Сначала разберёмся с признаком-фактором 
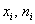
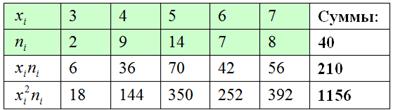
Вычислим среднее значение 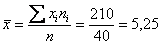
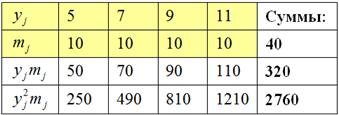
Аналогично, берём игрековые значения из комбинационной таблицы и заполняем расчетную таблицу для признака-результата 
после чего рассчитываем нужные показатели:
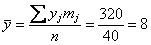
Теперь найдём среднее значение 
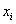
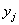
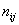
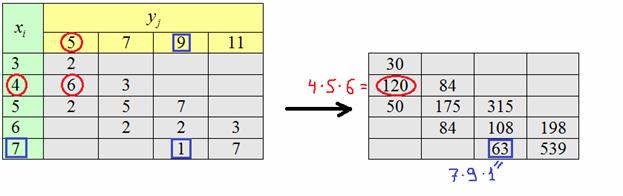
Вычислим сумму этих произведений: 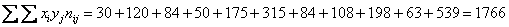
и искомую среднюю:
Таким образом, линейный коэффициент корреляции:
В результате получено положительное число и, согласно шкале Чеддока, существует сильная прямая линейная корреляционная зависимость 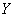
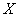
Вычислим коэффициент детерминации: 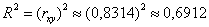
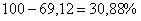
В статье об индексе корреляции и детерминации я более подробно разберу построенную модель, и тогда последний вывод станет понятнее (для тех, кому он не очень понятен).
3) Найдём уравнение 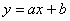
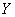
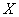
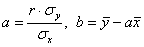
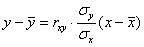
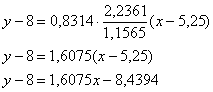
примерно:
Полученное уравнение показывает, что при увеличении стоимости основных фондов на 1 млрд. руб. суточная переработка сырья увеличивается в среднем на 1,61 тысяч центнеров.
Это очень важный вывод, который часто требуется в заданиях, по сути, смысл коэффициента «а».
Найдём пару удобных точек для построения графика: 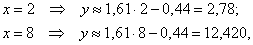
отметим их на чертеже (красный цвет) и аккуратно проведём линию регрессии, её, как правило, изображают на том же чертеже: 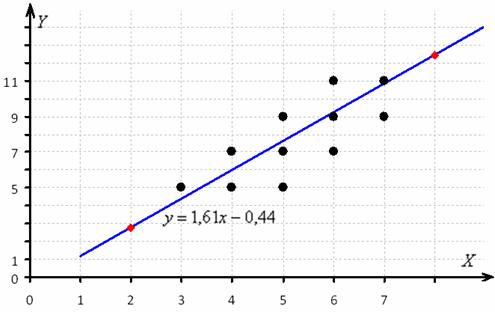
Спрогнозируем среднюю суточную переработку сырья при стоимости основных фондов в 9 млрд. руб.:
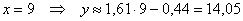
Ещё раз подчёркиваю, что уравнение регрессии возвращает нам среднее, а точнее среднеожидаемое значение 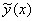
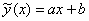
Теперь видео о том, как быстро расправиться с этой задачей:

Для желающих сразу решить эту задачу есть калькулятор.
Помимо рассмотренного, существует второе уравнение линейной регрессии – 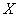
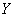
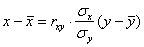
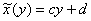
Чисто формально эта регрессия существует всегда, так, в рассмотренной задаче признак 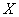
Здесь в уравнении регрессии 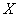
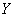
График регрессии 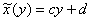
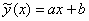
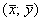
Следует добавить, что второе уравнение регрессии можно построить и для случая несгруппированных данных (см. задачи предыдущего урока о корреляции). Формула та же.
И я предлагаю вам потренироваться самостоятельно:
Известны следующие данные:
Найти линейный коэффициент корреляции и уравнения регрессии 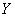
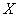
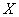
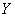
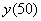
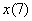
Обратите внимание, что в условии ничего не сказано о признаках 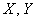
Все числа уже в Экселе и вам остаётся выполниться вычисления; ничего страшного, если получится не очень красиво, важно наработать сам навык. Краткое решение для сверки чуть ниже.
И я вас поздравляю! – на этом «обязательная часть программы» завершена, надеюсь, корреляционно-регрессионный «минимум» освоен успешно.
Для читателей с углублённым изучением статистики и просто энтузиастов запланирована статья об Индексе корреляции и проверке значимости коэффициентов (там на самом деле много ещё чего). Далее поговорим о моделях нелинейной регрессии, ранговой корреляции Спирмена, коэффициенте корреляции Фехнера. И вишенка на торте, точнее, тыква на голове:))
Множественная корреляция и модель двухфакторной регрессии.
Впрочем, это пока ориентировочные планы.
До скорых встреч!
Решения и ответы:
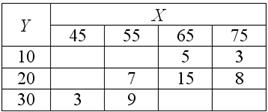
Пример 70. Решение: вычислим частоты по каждому признаку: 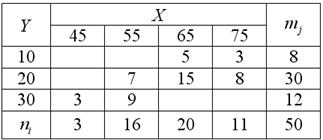
Линейный коэффициент корреляции найдём по формуле 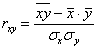
Заполним расчётную таблицу для признака 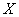
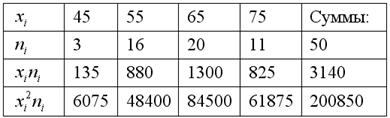
Вычислим среднее значение 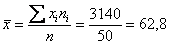
Заполним расчётную таблицу для признака 
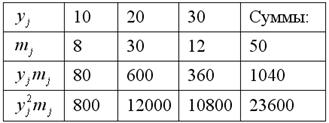
Вычислим 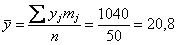
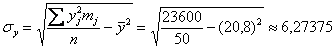
Вычислим произведения 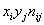
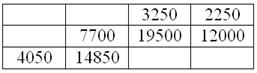
их сумму 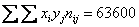
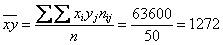
Вычислим линейный коэффициент корреляции: 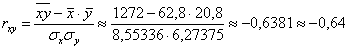
Составим уравнение линейной регрессии 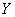
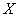
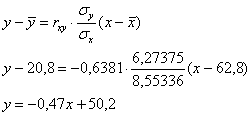
Полученное уравнение показывает, что при увеличении «икс» на 1 единицу «игрек» в среднем уменьшается примерно на 0,47 единицы.
Составим уравнение линейной регрессии 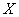
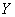
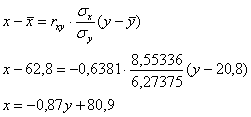
Полученное уравнение показывает, что при увеличении «игрек» на 1 единицу «икс» в среднем уменьшается примерно на 0,87 единицы.
Найдём точки для построения графиков: 
построим корреляционное поле и изобразим линии регрессии: 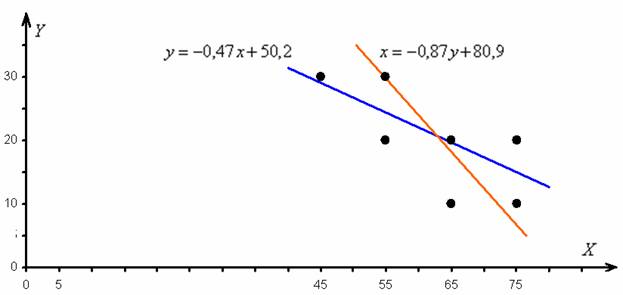
Линии регрессии пересекаются в точке
Вычислим:
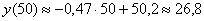
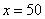
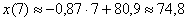
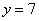
Примечание: вычисления местами не очень точные из-за округлений.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Источник