Построении линии пересечения поверхностей способом сферы

Построении линии пересечения поверхностей способом сферы

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

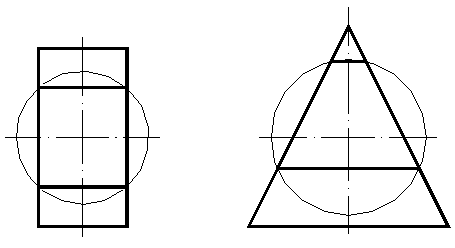
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей — прямые линии, а второй — когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

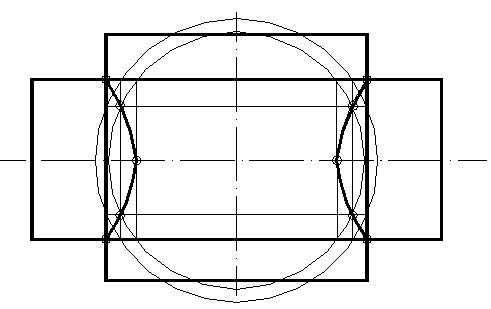
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

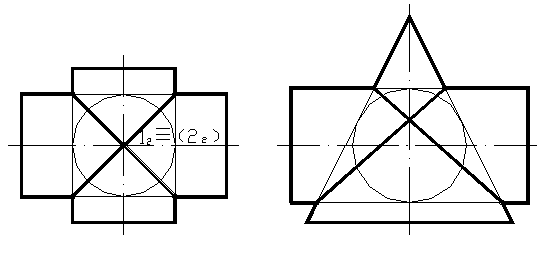
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Инженерная графика

Построение линий пересечения поверхностей способом вспомогательных сфер

В некоторых случаях для построения линий пересечения геометрических тел удобно применять способ вспомогательных сфер. В отличие от способа вспомогательных секущих поверхностей метод вспомогательных сфер имеет определенное преимущество, поскольку при построении фронтальной проекции линии пересечения поверхностей не используются другие проекции пересекающихся поверхностей геометрических тел (рис. 1).

Вспомогательные сферические поверхности для построения линий пересечения геометрических тел можно применять лишь при следующих условиях:

• пересекающиеся поверхности должны быть поверхностями тел вращения;
• оси поверхностей вращения должны пересекаться, при этом точка пересечения осей является центром вспомогательных сфер;
• оси поверхностей вращения должны быть параллельны какой-нибудь из плоскостей проекций.

Примеры применения вспомогательных сфер при построении линии пересечения геометрических тел приведены на рис. 1 а, б.

На рис. 1, а показано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом. Вспомогательные сферы проводят из точки О’ пересечения осей цилиндров.
Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О’ проводят сферическую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса.
Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр – по окружностям диаметра АВ.

В пересечении полученных проекций окружностей – отрезков a’b’ и c’d’ – находят проекцию 2′ промежуточной точки линии пересечения.

Вспомогательные сферы могут иметь радиусы в определенных пределах, позволяющих использовать их для построения общих точек пересекающихся тел. Пределы радиусов вспомогательных сфер находят следующим образом (рис. 1, а и б):

• окружность сферы наибольшего радиуса должна пересекаться с контурными образующими I-I и II-II цилиндров;
• окружность сферы наименьшего радиуса должна быть касательной к одной из данных пересекающихся поверхностей и обязательно пересекаться с образующими других поверхностей.

Если поверхности двух конусов (рис. 2) описаны около шара, то они касаются шара по двум окружностям, которые пересекаются в двух точках. Эти точки проецируются на фронтальную плоскость проекций в точку р’. Плоскости, в которых лежат эти окружности, пересекаются по прямой, соединяющей точки пересечения линий касания конусов с шаром.
Окружности проецируются на фронтальную плоскость проекций в виде прямых линий.

Соединив очевидную точку s’ пересечения конусов с точкой р’, получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.

Разберем второй подобный пример.
Если два прямых круговых цилиндра с осями, пересекающимися в точке О’ (рис. 2, б), описаны около шара с центром в точке О, то фронтальная проекция шара будет окружностью, касательной к контурным образующим цилиндров.
Линии пересечения поверхностей этих цилиндров представляют собой эллипсы, фронтальные проекции которых изображаются в виде прямых линий a’b’ и c’d’.

Источник

66. Построение линии пересечения поверхностей способом вспомогательных сфер

При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, со-осные с данными поверхностями.

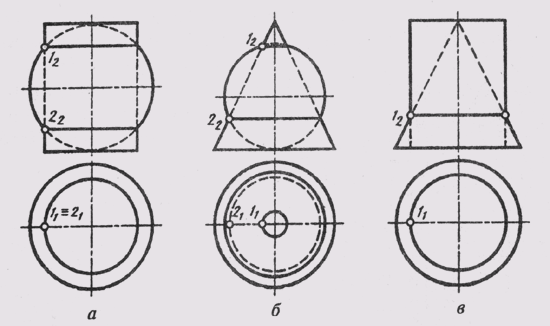
К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, б) и соосные цилиндр и конус (рис. 134, в).

Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов.

Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения.

Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.

При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:

1) пересечение поверхностей вращения;

2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;

3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.

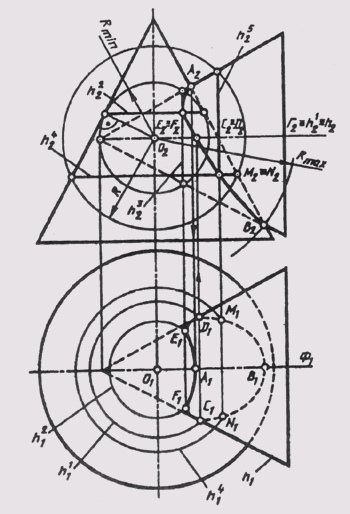
Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф₁) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П₂или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h’, лежащих в одной вспомогательной секущей плоскости Г(Г₂), определены точки видимости С и D линии пересечения относительно плоскости П₁. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О₁; О₂), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах

Rmin 2 ) и пересекающей другую (по окружности h 3 ).

Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:

Промежуточная сфера радиуса R пересекает поверхности по окружностям h 4 и h 5 , в пересечении которых находятся точки Ми N:

Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.

Источник

Построение линий пересечения поверхностей способом вспомогательных секущих сфер

Две любые соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения главных полумеридианов этих поверхностей. При этом плоскости окружностей сечения перпендикулярны оси поверхностей вращения, а центры окружностей принадлежат этой оси. Поэтому если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпен­дикулярных проекциям оси вращения.

В качестве вспомогательной секущей поверхности вращения целесообразно использовать удобную для вычерчивания сферическую поверхность, центр которой должен принадлежать оси поверхности вращения (рис. 1.73). Здесь сфера Σ (i,m) пересекается с поверхностью вращения Ф(i,n) по окружностям, т. к. полумеридианы поверхности вращения и сферы имеют две точки пересечения – A и В.

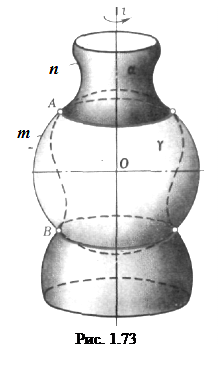
При построении линий пересечения двух поверхностей способом вспомогательных секущих сфер возможны два случая. В одном из них используют сферы, проведенные из одного общего для всех сфер центра, а в другом – сферы, проведенные из разных центров. В первом случае имеем способ концентрических сфер, во втором – способ эксцентрических сфер.

Рассмотрим каждый случай в отдельности.

1.7.4.1.Способ вспомогательных секущих концентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности вращения;

— оси поверхностей вращения пересекаются;

— плоскость, образованная пересекающимися осями (общая плоскость симметрии поверхностей), параллельна одной из плоскостей проекций. Именно на этой плоскости проекций и проводят вспомогательные секущие сферы, центр которых лежит в точке пересечения осей.

Рассмотрим пример. Построить линию пересечения цилиндра и конуса вращения, оси которых i и j пересекаются в некоторой точке Ои параллельны плоскости проекций П₂ (рис. 1.74).

Вначале должны быть построены некоторые опорные точки. Так как обе данные поверхности имеют общую плоскость симметрии, параллельную плоскости проекций П₂, то их контур­ные образующие, по отношению к плоскости П₂, пересекаются. Точки А, В, С и Dпересечения этих образующих являются точками видимости линии пересечения поверхностей. Эти точки ограничивают фронтальную проекцию линии пересечения.

Далее следует определить радиусы максимальной и минимальной сфер, пригодных для отыскания точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от проекции О₂ центра сфер до наибо­лее удаленной точки пересечения очерковых образующих, в данном случае до точки A₂.

Чтобы определить радиус наименьшей сферы R_min, необходимо провести через точку О₂нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет R_min. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а совторой – пересекаться. Если же взять в качестве R_min меньший отрезок, то одна из данных поверхностей с такой сферой не пересечется. В данном примере сферой минимального радиуса будет сфера, касающаяся цилиндрической поверхности. Эта сфера касается цилиндрической поверхности по окружности 1 – 2; коническую поверхность она пересекает по двум окружностям 3 – 4и 5 – 6. Точки Е, Fи G, Нпересечения этих ок­ружностей будут точками искомой линии пересечения.

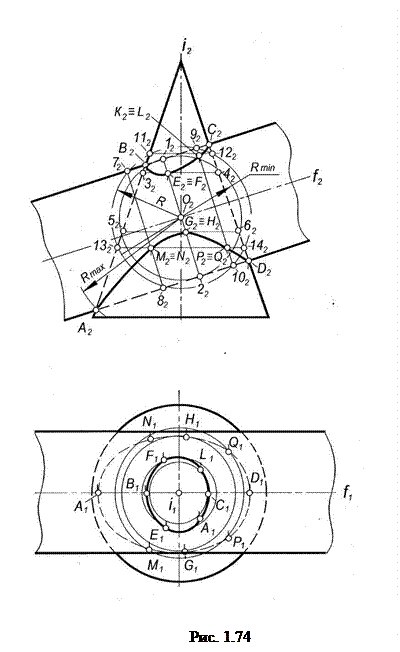
Для построения других точек линии пересечения проводят несколько концентрических сфер с центром в точке О, причем радиус Rэтих сфер должен изменяться в пределах R_min

1.7.4.2.Способ вспомогательных секущих эксцентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности, которые имеют общую плоскость симметрии;

— каждая из этих поверхностей должна содержать семейство окружностей, по которым ее могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Рассмотрим пример. Построить линию пересече­ния поверхности тора с конической поверхностью вращения, которые имеют общую фронтальную плоскость симметрии (рис. 1.75).

По аналогии с предыдущей задачей строим точки А и В пересечения контура поверхности тора с контуром конической поверхности. Точка А является наивысшей точкой искомой линии, а точка В – наинизшей.

Для построения произвольных точек линии пересечения в данной задаче нельзя воспользоваться способом вспомогательных концентрических сфер: хотя обе поверхности и являются поверхностями вращения, но их оси i 1 и i 2 не пересекаются. Способом же эксцентрических сфер, центры которых находятся в различных точках оси i 2 конической поверхности, можно найти сколько угодно произвольных точек линии пересечения.

Действительно, у поверхности тора, кроме семейства окружностей (параллелей), расположенных в плоскостях, перпендикулярных оси i 1 , имеется семейство окружностей (меридианов), расположенных в плоскостях, проходящих через ось i 1 . Центры сфер, пересекающих поверхность тора по этим окружностям, будут нахо­диться на перпендикулярах к плоскостям этих окружностей, проведенных через их центры С 1 , С 2 , С 3 , . . Поэтому если взять центры эксцентрических сфер в точках О 1 , О 2 , О 3 , . пересечения этих перпендикуляров с осью i 2 конической поверхности, то сферы соответствующих радиусов пересекут обе данные поверхности по окружностям. Точки пересечения окружностей обеих поверхностей, принадлежащих одной и той же сфере, и будут точками искомой линии пересечения.

На рис. 1.75 проведены три эксцентрические сферы из центров О 1 , О 2 и О 3 , с помощью которых найдены случайные точки линии пересечения. Так, для построения точек Ми Nпроведен меридиан 3 – 4поверхности тора, расположенный во фронтально проецирующей плоскости, проходящей через ось i 1 (i₂ 1 ), и из его центра С 1 (С_г 1 )восстановлен перпендикуляр к этой плоскости. В точке О 1 (О₂ 1 ) пересечения перпендикуляра с осью i 2 (i₂ 2 ) и будет находиться центр вспомогательной сферы. Если теперь провести сферу с центром в точке О 1 (О₂ 1 ) такого радиуса R, чтобы ей принадлежала окружность 3 – 4, то эта сфера, пересекая коническую поверхность по некоторой окружности 1 – 2, определит в пересечении окружностей 1 – 2 и 3 – 4 искомые точки Ми N.

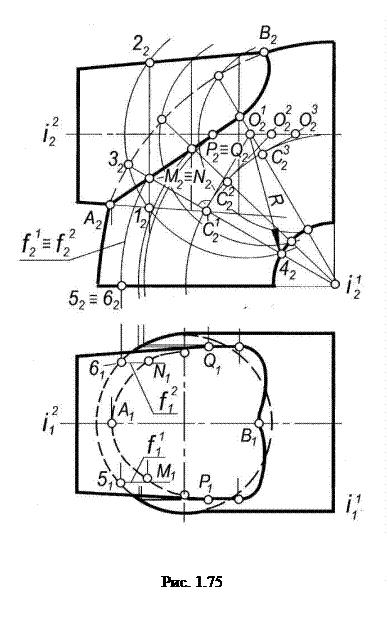
Горизонтальные проекции точек пересечения можно найти с помощью графически простых линий поверхности тора, которыми являются ее параллели. Так, горизонтальные проекции М₁ и N₁ точек Ми N построены при помощи параллелей j 1 и j 2 поверхности тора. Точки видимо­сти Ри Qконической поверхности для плоскости P₁ построены приближенно, их фронтальные проекции найдены в пересечении фронтальных проекций линии пересечения и оси i 2 конуса.

Источник