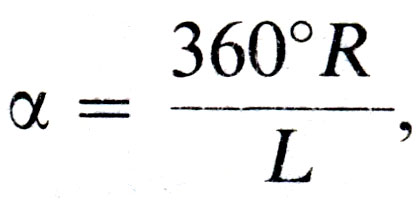Построение разверток способы построения разверток поверхности
§ 24. Построение разверток поверхностей тел
Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки.
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике.
Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани. Истинные размеры ребер граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций (проецированием на дополнительную плоскость), приведенными в предыдущем параграфе.
Рассмотрим построение разверток поверхности некоторых простейших тел.
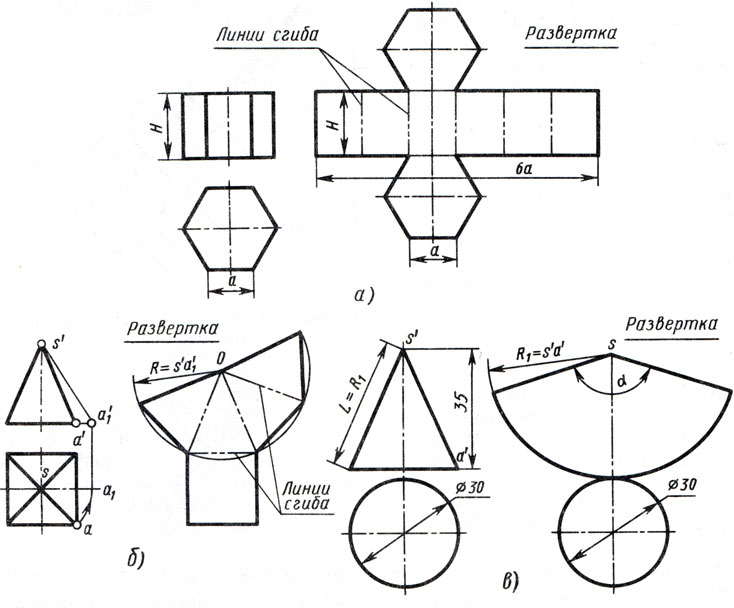
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух равных между собой многоугольников оснований. Для примера взята правильная прямая шестиугольная призма (рис. 176, а). Все боковые грани призмы — прямоугольники, равные между собой по ширине а и высоте Н; основания призмы — правильные шестиугольники со стороной, равной а. Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е. 6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба — штрихпунктирной с двумя точками.
Подобным образом можно построить развертки прямых призм с любой фигурой в основании.
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней — равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 176, б). Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинают с определения истинной величины наклонного ребра SA. Определив способом вращения (см. рис. 173, в) истинную длину наклонного ребра SA, равную s’a`1 (рис. 176, б), из произвольной точки О, как из центра, проводят дугу радиусом s’a`1. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Найденные точки соединяют прямыми с точкой О. Получив развертку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.
Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 176, в). Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, радиусом Rh равным образующей конуса sfd, очерчивают дугу окружности. В данном примере образующая, подсчитанная по теореме Пифагора, равна приблизительно
38 мм (L = √l5 2 + 35 2 = √l450 ≈ % 38 мм). Затем подсчитывают угол сектора по формуле
где R — радиус окружности основания конуса; L — длина образующей боковой поверхности конуса.
В данном примере α = 360°⋅15/38 ≈ 142,2°.
Этот угол строят симметрично относительно осевой линии с вершиной в точке s. К полученному сектору пристраивают круг с центром на осевой линии и диаметром, равным диаметру основания конуса.
Рис. 176. Чертеж разверток поверхностей геометрических тел
Источник
Развертка поверхности. Способы построения разверток
Цель лекции: изучение свойств развертки и способов построения разверток многогранников и поверхностей вращения
· Развертка поверхностей. Общие понятия.
· Способы построения разверток: методы триангуляции, нормального сечения и раскатки.
· Построение разверток гранных поверхностей и поверхностей вращения.
Развертка поверхностей. Общие понятия
| Развертка | плоская фигура, полученная при совмещении поверхности геометрического тела с плоскостью (без наложения граней или иных элементов поверхности друг на друга). Развертку можно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой. |
| Основные свойства развертки | 1 Длины двух соответствующих линий поверхности и ее развертки равны между собой; 2 Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке; 3 Прямой на поверхности соответствует также прямая на развертке; 4 Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке; 5 Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической. |
Методы триангуляции, нормального сечения и раскатки
Построение разверток гранных поверхностей и поверхностей вращения
| Существует три способа построения развертки многогранных поверхностей: | ||
| 1-й способ | 2-й способ | 3-й способ |
| Способ триангуляции (треугольника) | Способ нормального сечения | Способ раскатки |
а) Развертка поверхности многогранника.
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Метод триангуляции
Пример 1. Развертка пирамиды (рисунок 13.1).
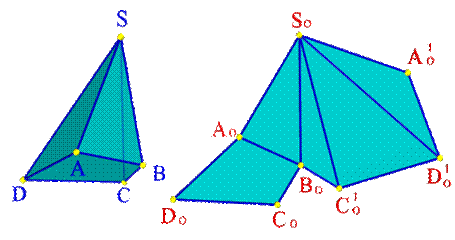
При построении развертки пирамиды применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника — основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих.
Рисунок 13.1. Пирамида и её развертка
Для этого необходимо знать натуральную величину ребер и сторон основания. Алгоритм построения можно сформулировать следующим образом (рисунок 13.2):
| 1 Определяют натуральную величину основания пирамиды (например, методом замены плоскостей проекций) |
| 2 Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S) |
| 3 Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рисунок 13.3). |
Рисунок 13.2. Определение истинной величины
основания и ребер пирамиды
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. Примером первой точки на рисунках служит точка К0 и КÎSАD, а иллюстрацией второго случая являются точки М0 и М0 * . Для определения точки К0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ (метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S0М0 и, наконец, точки К0.

Рисунок 13.3. Построение развертки пирамиды
Способ нормального сечения
В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.
Пример 2. Развертка призмы (рисунок 13.4).
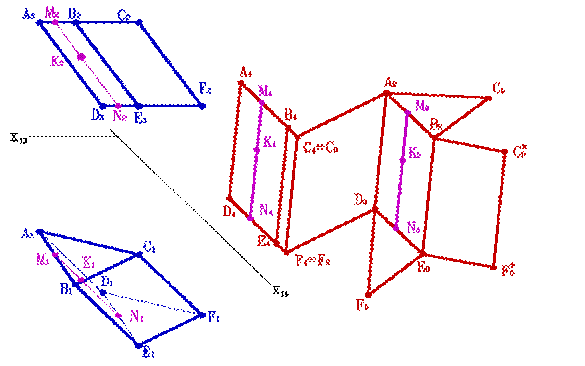
Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения – треугольника 1, 2, 3, а затем определяют истинную величину этого сечения. На примере она найдена методом вращения.
В дальнейшем строям отрезок 10-10 * , равный периметру нормального сечения. Через точки 10, 20, 30 и 10 * проводят прямые, перпендикулярные 10-10 * , на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.. Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание.
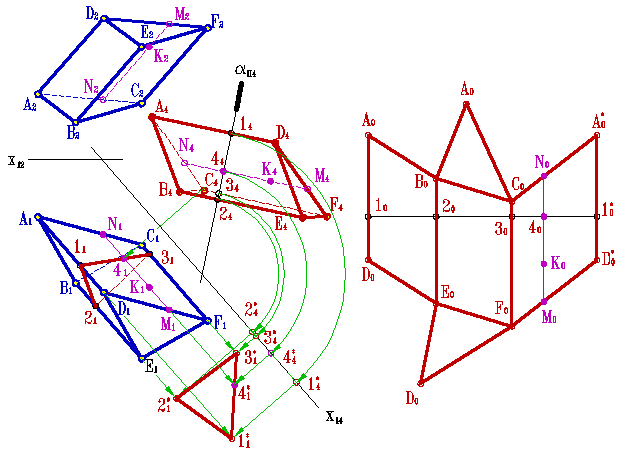
Способ раскатки
Пример 3. Развертка призмы, частный случай, когда основание призмы на одну из плоскостей проекций проецируется в натуральную величину (рисунок 13.5).
Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.
Рисунок 13.4. Развертка призмы способом нормального сечения

Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4.
При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения, т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4.
Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.
Когда грань ACDFстанет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.
Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.
Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.
Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке.
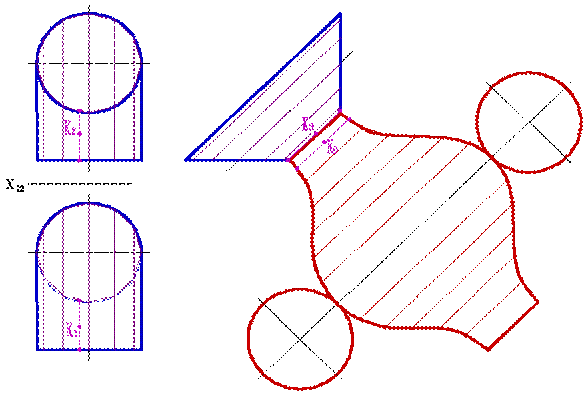
б) Развертка цилиндрической поверхности.
Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму (рисунок 13.6). Чем больше углов в призме, тем точнее развертка (при n →призма преобразуется в цилиндр).
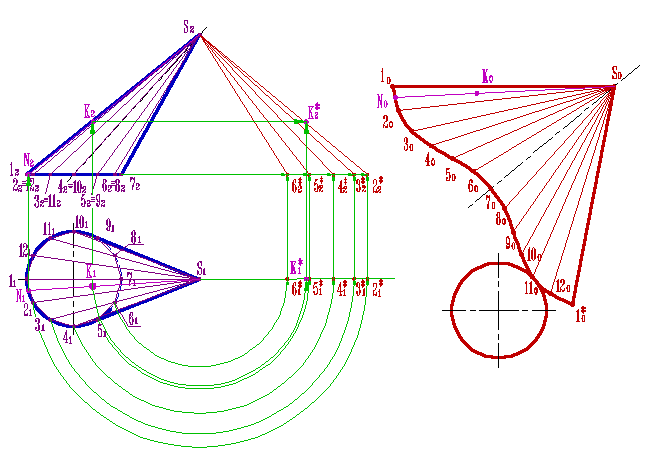
в) Развертка конической поверхности
Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду (рисунок 13.6).
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ=360 о r / l, где r – радиус окружности основания конуса.
Рисунок 13.6. Развертка цилиндрической поверхности

| Запомните! Задание | Существует три способа построения развертки: способ нормального сечения, раскатки и треугольника.Дайтехарактеристику каждому из способов. Внимательно рассмотрите примеры, приведенные в лекции. Выполните построения по рисункам 13.1…13.7. |
Контрольные вопросы
1 Что называют разверткой поверхности?
2 Какие поверхности называют развертывающимися и какие – неразвертывающимися?
3 Укажите основные свойства разверток
4 Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
5 Какие способы построения разверток многогранников вы знаете?
Источник