Построение развертки цилиндра может выполняться способом аппроксимации

Построение развертки цилиндра может выполняться способом аппроксимации

Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. При этом исходим из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки. Свойством развертываемости обладают многогранные поверхности и кривые линейчатые поверхности с ребром возврата: торсы, конические и цилиндрические.
Линейчатые косые и нелинейчатые поверхности этим свойством не обладают. Существуют различные способы построения их условных разверток при помощи аппроксимации.
Плоская фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой. Между поверхностью и ее разверткой существует взаимно-однозначное точечное соответствие (точке А на поверхности соответствует точка А’ на развертке, и наоборот), обладающее следующими свойствами (рис. 7.1):

1) длина участка АВ линии l на поверхности равна длине участка А’В’ соответствующей ей линии l на развертке;
2) угол между кривыми m и n на поверхности равен углу ‘ между соответствующими им кривыми m’ и n’ на развертке (углом между кривыми называется угол между касательными к ним в точке пересечения);
3) площадь отсека F поверхности равна площади соответствующего ему отсека F’ развертки.
В дифференциальной геометрии доказывается, что второе и третье свойства являются следствием первого. Первое свойство вытекает из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки.
Из рассмотренных свойств следует:
1) прямой линии (a) на поверхности соответствует прямая (а’) на развертке;
2) прямым, параллельным (а b) на поверхности, соответствуют прямые, параллельные (a’ b’) на развертке.
Однако оба указанных свойства обратной силы не имеют, т. е. не всякой прямой на развертке соответствует прямая на поверхности. Примерами этого могут служить цилиндрическая винтовая линия, параллели поверхности вращения. Если кривой линии, принадлежащей поверхности, соответствует прямая на развертке, то эта кривая линия является геодезической для данной поверхности.

7.1. ПОСТРОЕНИЕ РАЗВЕРТОК МНОГОГРАННИКОВ

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников — граней, а иногда и некоторых других элементов. Ребра многогранника условно разделяются на боковые и стороны основания.
Построение развертки пирамиды
Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 7.2 ) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.
Рис. 7.2

У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П₁ в истинную величину. Длины боковых ребер определены построением прямоугольных треугольников
S₂M₀C₀, S₂M₀B₀ и S₂M₀А₀, у которых одним катетом является высота пирамиды (S₂М₀ — разность высот точки S и точек А, В, С), а другим — горизонтальная проекция соответствующего ребра.
(/M₀C₀/ = /S₁C₁/; /M₀B₀/ = /S₁B₁/; /M₀A₀/ = /S₁A₁/; /M₀K₀/ = /S₁K₁/).
Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П₁. Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание (АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. На рис. 7.3 показана динамическая схема развертки наклонной пирамиды.

Построение развертки призмы
Наклонная призма изображена на рис. 7.4. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П₁ без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.

Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью (₂), перпендикулярной к ребрам, и определим истинную величину сечения способом замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней. Теперь приступаем к построению развертки. На свободном месте чертежа проводим горизонтальную прямую m и откладываем на ней отрезки /1 — 2/ = /1₄ — 2₄/, /2 — З/ = /2₄ — 3₄/ и /3 — 1/ = /3₄ — 1₄/.

Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы /А1/ = /А₂1₂/ и /1К/ = /1₂К₂/, /В2/ = /В₂2₂/ и /2L/ = /2₂L₂/ и т. п.
Соединив концы построенных отрезков, получим развертку боковой поверхности призмы. Присоединив к ней оба основания, получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа. На рис. 7.5 показана динамическая схема развертки поверхности наклонной призмы.

7.2. ПОСТРОЕНИЕ РАЗВЕРТОК КРИВЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ

Построение точных разверток кривых развертывающихся поверхностей сложно и, как правило, не вызывается практической необходимостью. Поэтому обычно строят приближенные развертки поверхностей, вполне пригодные для практических целей. Основным способом построения приближенных разверток развертывающихся поверхностей (кроме цилиндрических) является способ триангуляции поверхности. Способ триангуляции состоит в том, что кривая поверхность заменяется многогранной поверхностью, состоящей из треугольных граней. Рассмотрим применение способа триангуляции к построению развертки эллиптического конуса, изображенного на чертеже (рис. 7.6).

Триангуляция конической поверхности осуществляется вписыванием в нее пирамидальной поверхности, которая определяется ломаной 1 — 2 — 3 — 4, . вписанной в направляющую кривую конуса, и вершиной S. Развертка этой n-угольной пирамиды и принимается за развертку конуса. Все построения на чертеже (рис. 7.6) выполняются аналогично построениям на чертеже (рис.7.2). Ломаная линия 1 — 2 — 3 — 4, . получающаяся на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки.
Развертка прямого кругового конуса, образующая которого равна / l / и радиус основания / r /, имеет форму кругового сектора с радиусом равным / l / и центральным углом = 360 o &#124 r &#124 / &#124 l &#124 — (рис. 7.7).

На рис. 7.8 показана динамическая схема развертки прямогo кругового конуса.
При построении разверток цилиндрических поверхностей способ триангуляции, как правило, не применяется.

Цилиндрическая поверхность заменяется (аппроксимируется) вписанной в нее призматической поверхностью, которая определяется ломаной 1 — 2 — 3 — 4, . вписанной в направляющую кривую цилиндра, и направлением образуюших. Развертка этой п-угольной призмы и принимается за развертку цилиндра (рис. 7.9).
Все построения выполняются, как на рис. 7.4. Ломаная линия
1 — 2 — 3 — 4, . получающаяся на развертке призмы, заменяется плавной кривой, проходящей через те же точки. Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник со сторонами, соответственно равными 2пr и h, где r — радиус окружности основания цилиндра, а h — его высота. На рис. 7.10 показана динамическая схема развертки прямогo кругового цилиндра.

7.3. ПОСТРОЕНИЕ УСЛОВНЫХ РАЗВЕРТОК НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ

Развертку неразвертывающейся поверхности построить нельзя. Для построения условной развертки такой поверхности применяют метод аппроксимации, который заключается в следующем.
Данная неразвертываюшаяся поверхность Ф разбивается на некоторые отсеки. Каждый из этих отсеков заменяется отсеком кривой развертывающейся поверхности. Совокупность всех отсеков развертывающихся поверхностей называется обводом Ф’ поверхности Ф. С помощью триангуляции обвод Ф’ заменяется обводом Ф» гранных поверхностей. Развертка гранных поверхностей, образующих обвод Ф», принимается за условную развертку поверхности Ф. При свертывании такой развертки, кроме изгибания, необходимо произвести частичное растяжение или сжатие отдельных ее участков.
Рассмотрим применение этого способа на примере построения условной развертки сферы.
Разделим поверхность сферы (рис. 7.11, а) на некоторое число (например, шесть) одинаковых отсеков при помощи осевых плоскостей , , .

Поверхность каждого отсека сферы заменим отсеком описанной цилиндрической поверхности. В результате поверхность сферы заменяется обводом (составной поверхностью), составленным из отсеков прямых круговых цилиндров.
Поверхность каждого отсека цилиндрической поверхности заменим отсеком вписанной призматической поверхности (рис. 7.11, б). В результате обвод, составленный из отсеков цилиндров, заменяется обводом, составленным из гранных поверхностей (отсеков прямых призм).
Строим развертку каждого отсека призматической поверхности. На чертеже (рис. 7.11, в) показана развертка одного из них. Затем ломаная 1 — 3 — 5 — 7. заменяется плавной кривой, проходящей через те же точки (рис. 7.11, г). Полученная фигура принимается за условную развертку отсека сферы. Полная развертка будет состоять из шести таких фигур (рис. 7.11, д).

На рис. 7.12 показана динамическая сцена приближенной развертки сферы.
Применяя в качестве аппроксимирующих поверхностей цилиндрические, конические или торсовые поверхности, аналогично можно строить условные развертки других неразвертывающихся поверхностей.

Источник

Построение развертки цилиндра может выполняться способом аппроксимации

Построение развертки цилиндра может выполняться способом аппроксимации

Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. При этом исходим из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки. Свойством развертываемости обладают многогранные поверхности и кривые линейчатые поверхности с ребром возврата: торсы, конические и цилиндрические.
Линейчатые косые и нелинейчатые поверхности этим свойством не обладают. Существуют различные способы построения их условных разверток при помощи аппроксимации.
Плоская фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой. Между поверхностью и ее разверткой существует взаимно-однозначное точечное соответствие (точке А на поверхности соответствует точка А’ на развертке, и наоборот), обладающее следующими свойствами (рис. 7.1):

1) длина участка АВ линии l на поверхности равна длине участка А’В’ соответствующей ей линии l на развертке;
2) угол между кривыми m и n на поверхности равен углу ‘ между соответствующими им кривыми m’ и n’ на развертке (углом между кривыми называется угол между касательными к ним в точке пересечения);
3) площадь отсека F поверхности равна площади соответствующего ему отсека F’ развертки.
В дифференциальной геометрии доказывается, что второе и третье свойства являются следствием первого. Первое свойство вытекает из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки.
Из рассмотренных свойств следует:
1) прямой линии (a) на поверхности соответствует прямая (а’) на развертке;
2) прямым, параллельным (а b) на поверхности, соответствуют прямые, параллельные (a’ b’) на развертке.
Однако оба указанных свойства обратной силы не имеют, т. е. не всякой прямой на развертке соответствует прямая на поверхности. Примерами этого могут служить цилиндрическая винтовая линия, параллели поверхности вращения. Если кривой линии, принадлежащей поверхности, соответствует прямая на развертке, то эта кривая линия является геодезической для данной поверхности.

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников — граней, а иногда и некоторых других элементов. Ребра многогранника условно разделяются на боковые и стороны основания.
Построение развертки пирамиды
Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 7.2 ) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.
Рис. 7.2

У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П₁ в истинную величину. Длины боковых ребер определены построением прямоугольных треугольников
S₂M C , S₂M B и S₂M А , у которых одним катетом является высота пирамиды (S₂М — разность высот точки S и точек А, В, С), а другим — горизонтальная проекция соответствующего ребра.
(/M C / = /S₁C₁/; /M B / = /S₁B₁/; /M A / = /S₁A₁/; /M K / = /S₁K₁/).
Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П₁. Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание (АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. На рис. 7.3 показана динамическая схема развертки наклонной пирамиды.

Построение развертки призмы
Наклонная призма изображена на рис. 7.4. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П₁ без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.

Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью (₂), перпендикулярной к ребрам, и определим истинную величину сечения способом замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней. Теперь приступаем к построению развертки. На свободном месте чертежа проводим горизонтальную прямую m и откладываем на ней отрезки /1 — 2/ = /1₄ — 2₄/, /2 — З/ = /2₄ — 3₄/ и /3 — 1/ = /3₄ — 1₄/.

Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы /А1/ = /А₂1₂/ и /1К/ = /1₂К₂/, /В2/ = /В₂2₂/ и /2L/ = /2₂L₂/ и т. п.
Соединив концы построенных отрезков, получим развертку боковой поверхности призмы. Присоединив к ней оба основания, получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа. На рис. 7.5 показана динамическая схема развертки поверхности наклонной призмы.

7.2. ПОСТРОЕНИЕ РАЗВЕРТОК КРИВЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ

Построение точных разверток кривых развертывающихся поверхностей сложно и, как правило, не вызывается практической необходимостью. Поэтому обычно строят приближенные развертки поверхностей, вполне пригодные для практических целей. Основным способом построения приближенных разверток развертывающихся поверхностей (кроме цилиндрических) является способ триангуляции поверхности. Способ триангуляции состоит в том, что кривая поверхность заменяется многогранной поверхностью, состоящей из треугольных граней. Рассмотрим применение способа триангуляции к построению развертки эллиптического конуса, изображенного на чертеже (рис. 7.6).

Триангуляция конической поверхности осуществляется вписыванием в нее пирамидальной поверхности, которая определяется ломаной 1 — 2 — 3 — 4, . вписанной в направляющую кривую конуса, и вершиной S. Развертка этой n-угольной пирамиды и принимается за развертку конуса. Все построения на чертеже (рис. 7.6) выполняются аналогично построениям на чертеже (рис.7.2). Ломаная линия 1 — 2 — 3 — 4, . получающаяся на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки.
Развертка прямого кругового конуса, образующая которого равна / l / и радиус основания / r /, имеет форму кругового сектора с радиусом равным / l / и центральным углом = 360 o &#124 r &#124 / &#124 l &#124 — (рис. 7.7).

На рис. 7.8 показана динамическая схема развертки прямогo кругового конуса.
При построении разверток цилиндрических поверхностей способ триангуляции, как правило, не применяется.

Цилиндрическая поверхность заменяется (аппроксимируется) вписанной в нее призматической поверхностью, которая определяется ломаной 1 — 2 — 3 — 4, . вписанной в направляющую кривую цилиндра, и направлением образуюших. Развертка этой п-угольной призмы и принимается за развертку цилиндра (рис. 7.9).
Все построения выполняются, как на рис. 7.4. Ломаная линия
1 — 2 — 3 — 4, . получающаяся на развертке призмы, заменяется плавной кривой, проходящей через те же точки. Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник со сторонами, соответственно равными 2пr и h, где r — радиус окружности основания цилиндра, а h — его высота. На рис. 7.10 показана динамическая схема развертки прямогo кругового цилиндра.

7.3. ПОСТРОЕНИЕ УСЛОВНЫХ РАЗВЕРТОК НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ

Развертку неразвертывающейся поверхности построить нельзя. Для построения условной развертки такой поверхности применяют метод аппроксимации, который заключается в следующем.
Данная неразвертываюшаяся поверхность Ф разбивается на некоторые отсеки. Каждый из этих отсеков заменяется отсеком кривой развертывающейся поверхности. Совокупность всех отсеков развертывающихся поверхностей называется обводом Ф’ поверхности Ф. С помощью триангуляции обвод Ф’ заменяется обводом Ф» гранных поверхностей. Развертка гранных поверхностей, образующих обвод Ф», принимается за условную развертку поверхности Ф. При свертывании такой развертки, кроме изгибания, необходимо произвести частичное растяжение или сжатие отдельных ее участков.
Рассмотрим применение этого способа на примере построения условной развертки сферы.
Разделим поверхность сферы (рис. 7.11, а) на некоторое число (например, шесть) одинаковых отсеков при помощи осевых плоскостей , , .

Поверхность каждого отсека сферы заменим отсеком описанной цилиндрической поверхности. В результате поверхность сферы заменяется обводом (составной поверхностью), составленным из отсеков прямых круговых цилиндров.
Поверхность каждого отсека цилиндрической поверхности заменим отсеком вписанной призматической поверхности (рис. 7.11, б). В результате обвод, составленный из отсеков цилиндров, заменяется обводом, составленным из гранных поверхностей (отсеков прямых призм).
Строим развертку каждого отсека призматической поверхности. На чертеже (рис. 7.11, в) показана развертка одного из них. Затем ломаная 1 — 3 — 5 — 7. заменяется плавной кривой, проходящей через те же точки (рис. 7.11, г). Полученная фигура принимается за условную развертку отсека сферы. Полная развертка будет состоять из шести таких фигур (рис. 7.11, д).

На рис. 7.12 показана динамическая сцена приближенной развертки сферы.
Применяя в качестве аппроксимирующих поверхностей цилиндрические, конические или торсовые поверхности, аналогично можно строить условные развертки других неразвертывающихся поверхностей.

Построение развертки цилиндра может выполняться способом аппроксимации

Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)

Необходимо построить развертку поверхностей и перенести линию пересечения поверхностей на развертку. В основе данной задачи рассматриваются поверхности (конуса и цилиндра) с их линией пересечения, приведенные в предыдущей задаче 8.

Для решения таких задач по начертательной геометрии необходимо знать:

— порядок и методы построения разверток поверхностей;

— взаимное соответствие между поверхностью и ее разверткой;

— частные случаи построения разверток.

Порядок решения задачи

1. Отметим, что разверткой называется фигура, получаемая в
результате разреза поверхности по какой-либо образующей и постепенного разгибания ее до полного совмещения с плоскостью. Отсюда развертка, прямого кругового конуса — сектор с радиусом, равным длине образующей, и основанием, равным длине окружности основания конуса. Все развертки строятся только из натуральных величин.

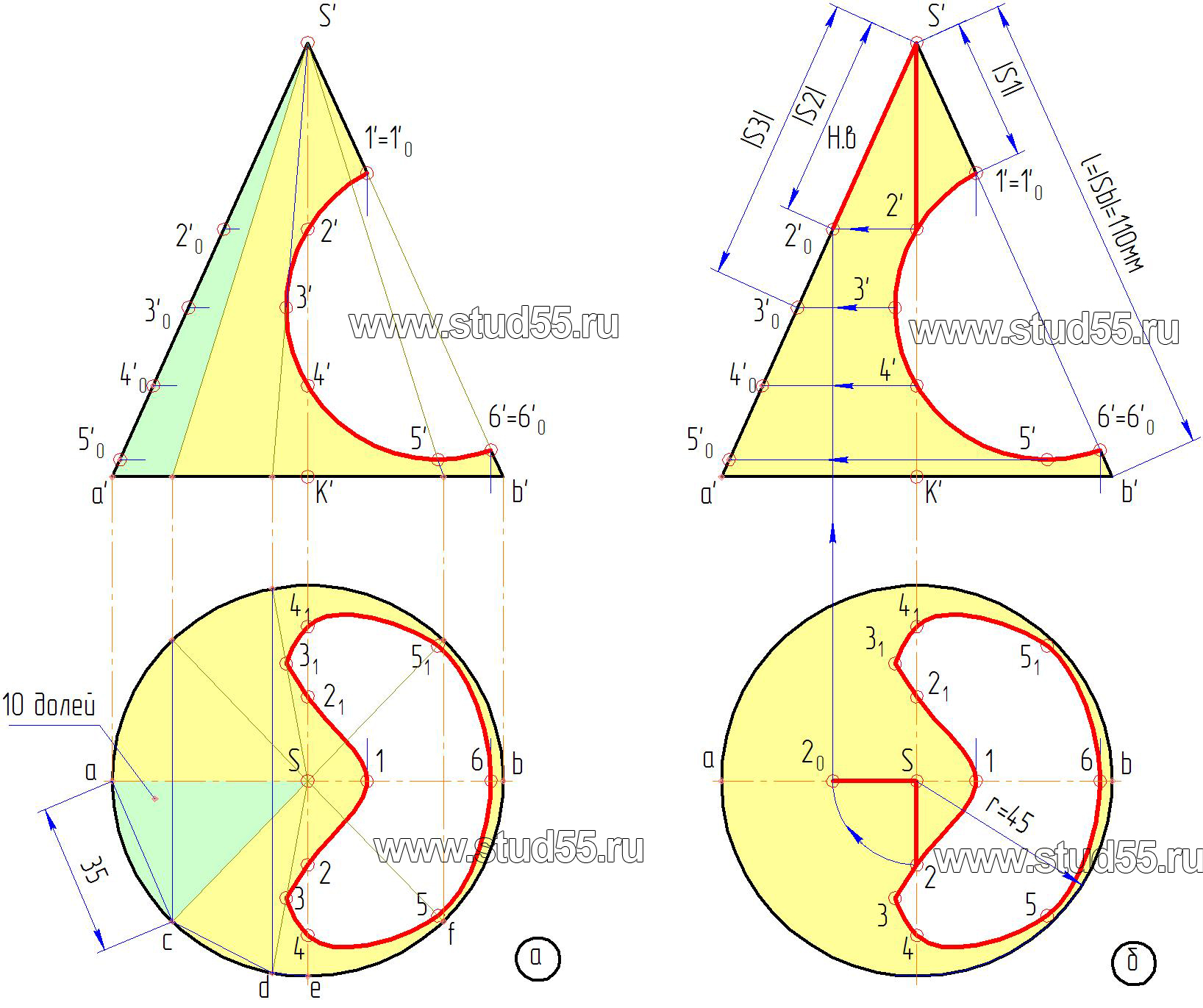
— длину окружности основания конуса, выраженную в натуральной величине делим на ряд долей: в нашем случае — 10, от количества долей зависит точность построения развертки (рис.9.1.а);

— откладываем полученные доли, заменяя их хордами, на длине
дуги, проведенной радиусом, равным длине образующей конуса l=|Sb|. Начало и конец отсчета долей соединяем с вершиной сектора — это и будет развертка боковой поверхности конуса.

Второй способ:

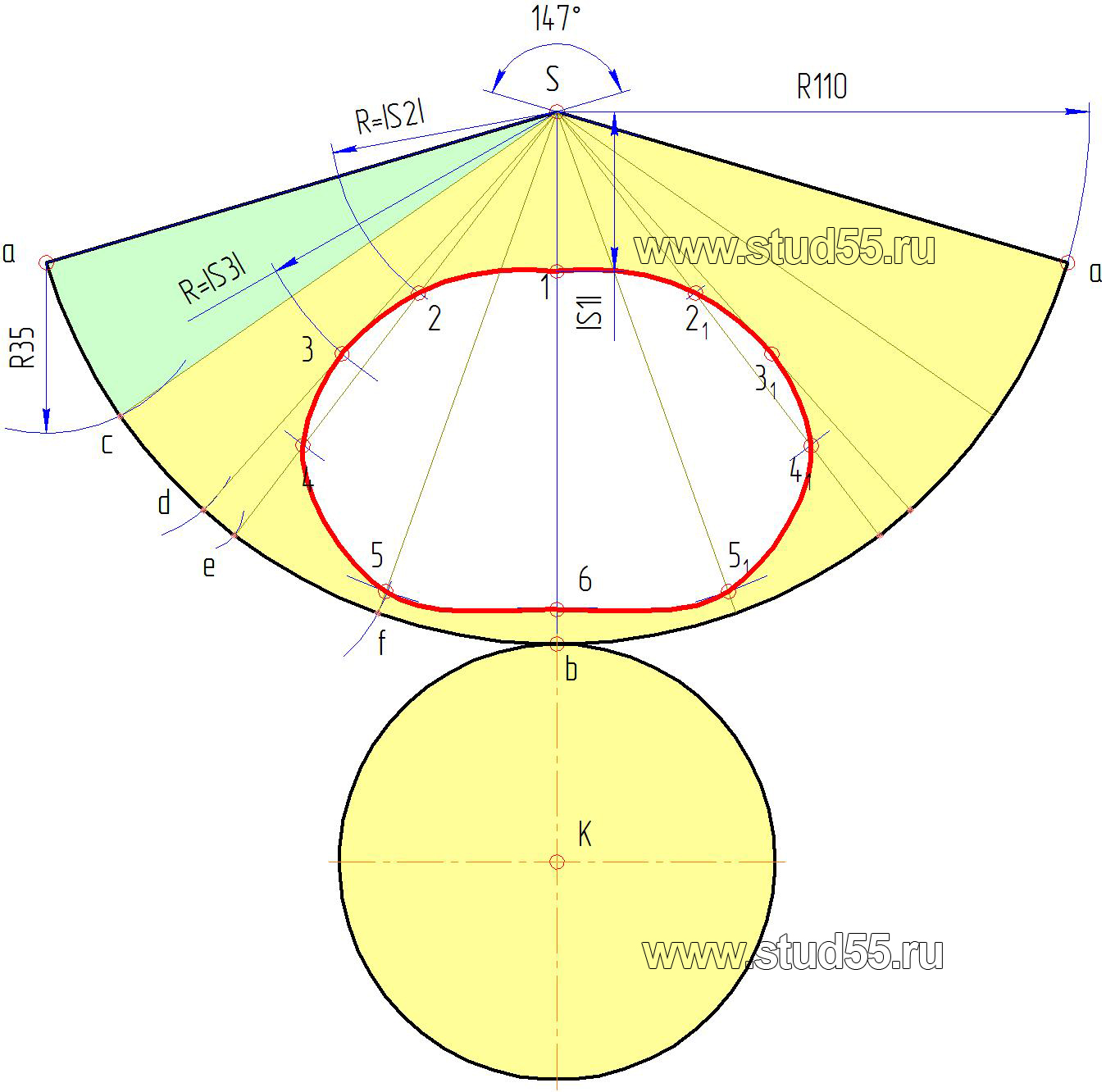
— строим сектор с радиусом, равным длине образующей конуса.
Заметим, что как в первом, так и во втором случае за радиус берется крайняя правая или левая образующие конуса l=|Sb|, т.к. они выражены в натуральной величине;

— при вершине сектора откладываем угол а, определяемый по формуле:

где r — величина радиуса основания конуса;

l — длина образующей конуса;

360 — постоянная переводная в градусы величина.

К сектору-развертке строим основание конуса радиуса r.

2. По условиям задачи требуется перенести линию пересечения
поверхностей конуса и цилиндра на развертку. Для этого используем свойства взаимной однозначности между поверхностью и ее разверткой, в частности, отметим, что каждой точке на поверхности соответствует точка на развертке и каждой линии на поверхности соответствует линия на развертке.

Отсюда вытекает последовательность перенесения точек и линий
с поверхности на развертку.

Для развертки конуса. Условимся, что разрез поверхности конуса произведен по образующей S’a’. Тогда точки 1, 2, 3,…6
будут лежать на окружностях (дугах на развертке) с радиусами соответственно равными величинам расстояний, взятым по образующей S’A’ от вершины S’ до соответствующей секущей плоскости с точками 1’, 2’, 3’…6’ -|S1|, |S2|, |S3|….|S6| (рис.9.1.б).

Положение точек на этих дугах определяется расстоянием, взятым с горизонтальной проекции от образующей Sa, по хорде до соответствующей точки, например до точки с, ас=35 мм (рис.9.1.а). Если расстояние по хорде и дуге сильно разнятся, то для уменьшения погрешности можно разделить большее количество долей и отложить их на соответствующие дуги развертки. Таким способом переносятся любые точки с поверхности на ее развертку. Полученные точки соединятся плавной кривой по лекалу (рис.9.3).

Для развертки цилиндра.

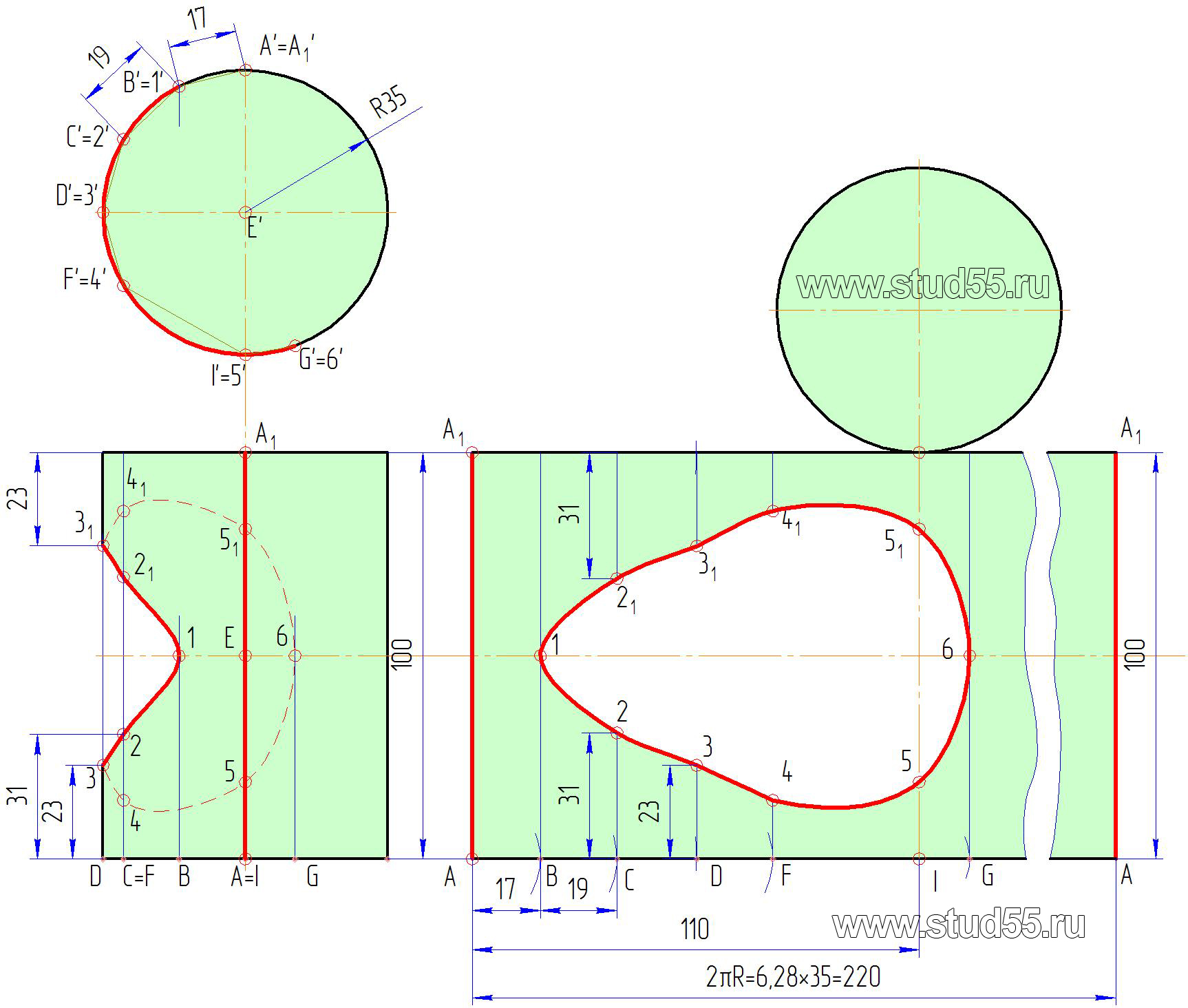
Развертка цилиндра есть прямоугольник с высотой, равной высоте образующей, и длиной, равной длине окружности основания цилиндра. Таким образом, для построения развертки прямого кругового цилиндра необходимо построить прямоугольник с высотой, равной высоте цилиндра, в нашем случае 100мм, и длиной, равной длине окружности основания цилиндра, определенной по известным формулам: C=2R=220мм, или делением окружности основания на ряд долей, как было указано выше. К верхней и нижней части полученной развертки пристраиваем основание цилиндра.

Условимся, что разрез произведен по образующей AA₁ (A’A’₁; AA1). Заметим, что разрез следует производить по характерным (опорным) точкам для более удобного построения. Учитывая, что длина развертки есть длина окружности основания цилиндра C, от точки A’=A’₁ разреза фронтальной проекции берем расстояние по хорде (если расстояние большое, то необходимо его разделить на доли) до точки B’ (в нашем примере — 17мм) и откладываем его на развертке (по длине основания цилиндра) от точки А. Из полученной точки В проводим перпендикуляр (образующую цилиндра). Точка 1 должна находиться на этом перпендикуляре) на расстоянии от основания, взятого с горизонтальной проекции до точки. В нашем случае точка 1 лежит на оси симметрии развертки на расстоянии 100/2=50мм (рис.9.4).

И так поступаем для нахождения на развертке всех других точек.

Подчеркнем, что расстояние по длине развертки для определения положения точек берется с фронтальной проекции, а расстояние по высоте — с горизонтальной, что соответствует их натуральным величинам. Полученные точки соединяем плавной кривой по лекалу (рис.9.4).

В вариантах задач, когда линия пересечения распадается на несколько ветвей, что соответствует полному пересечению поверхностей, способы построения (перенесения) линии пересечения на развертку аналогичны, описанным выше.

Источник