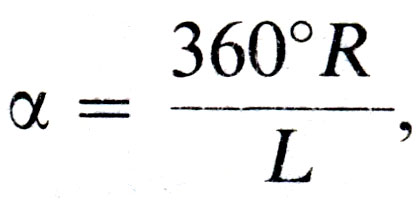Способ треугольников

Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

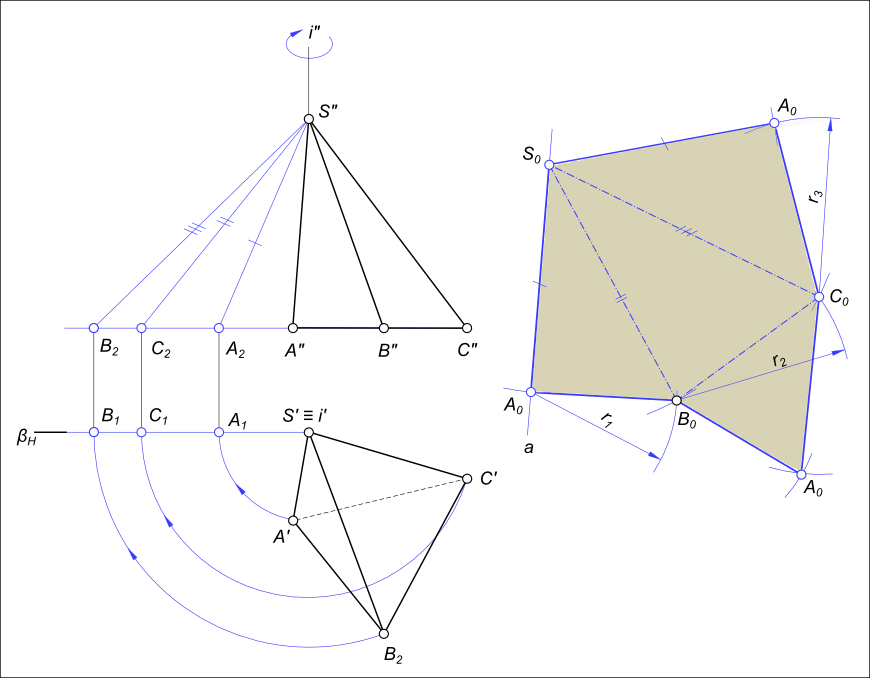
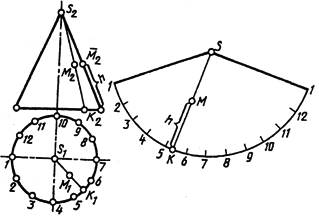
Способ треугольников используют для построения развертки поверхности пирамиды. Развертка боковой поверхности пирамиды — плоская фигура, состоящая из треугольников — граней пирамиды. Поэтому построение развертки поверхности пирамиды сводится к определению действительной величины ребер пирамиды и построению по трем известным сторонам треугольников — граней пирамиды.

Вращаем ребра вокруг оси i (i⊥H и i∋S) и совмещаем с плоскостью β (плоскость β║V β∋i). Выполняем определение действительных величин ребер пирамиды [S»A₂], [S»B₂], [S»C₂]. Приступая к построению развертки проводим произвольную прямую a через произвольную точку S₀. Откладываем на ней от точки S₀ отрезок [S₀A₀]≅ [S»A₂]. Из точки A₀ проводим дугу радиусом r₁=‌A`B`‌, а из точки S₀ — дугу радиусом R₁=‌S»B₂. Пересечение дуг укажет положение вершины B₀ ΔS₀A₀B₀ (ΔS₀A₀B₀≅ΔSAB — грани пирамиды). Аналогично определяем положение точек C₀ и A₀. Соединяя точки A₀B₀C₀A₀S₀, получим развертку боковой поверхности. Присоединив к какой-либо стороне (ребру) основание (ΔABC) — получаем полную развертку поверхности пирамиды SABC.

Способ треугольников использован для построения развертки поверхности усеченной пирамиды в графической работе №12: Графическая работа 12

Источник

Глава 11. Метрические задачи

Глава 11 Общие сведения Определение истинной величины расстояний Определение истинной величины углов Определение истинной величины плоской фигуры Построение разверток поверхностей Развертки пирамидальных и конических поверхностей Развертки призматических и цилиндрических поверхностей Вопросы

§ 73. Развертки пирамидальных и конических поверхностей

Развертки пирамидальных и конических поверхностей строят способом триангуляции (способом треугольников). Построение разверток этих поверхностей сводится к многократному построению истинных величин треугольников, из которых состоит поверхность развертываемой пирамиды или которой заменяют развертываемую коническую поверхность.

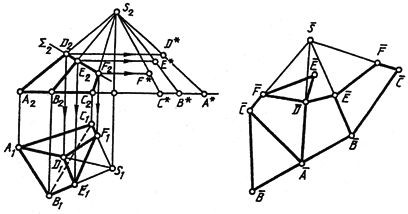
На рис. 148 построена полная развертка пирамиды SABC, усеченной фронтально проецирующей плоскостью Σ(Σ₂).

Сначала нужно построить развертку боковой поверхности всей пирамиды (фигуру S С А В С), состоящую из натуральных величин боковых граней. Для этого необходимо определить истинную величину боковых ребер. На рис. 148 истинная величина ребер AS, BS, CS построена способом прямоугольного треугольника. В данном случае одним катетом взято превышение точки S над точками А, В и С, а вторым катетом — горизонтальная проекция соответствующего ребра. Гипотенузы S₂C*, S₂B* и дают истинную величину боковых ребер. Основание пирамиды расположено горизонтально, поэтому на плоскости П₁ имеем истинную величину и самого основания ∆АВС, и его сторон АВ, ВС, АС.

Каждая боковая грань на развертке строится как треугольник по трем сторонам. CS — самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.

Для нанесения на развертку точек D, E и F, соответствующих вершинам сечения пирамиды плоскостью Σ, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники A B C и D E F, дающие истинную величину основания и сечения пирамиды.

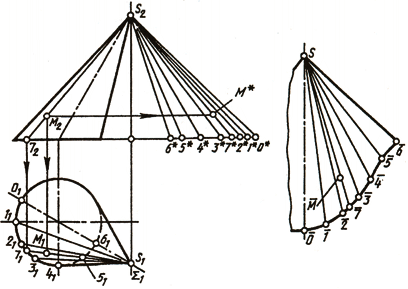
На рис. 149 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Σ. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.

Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 149. От оси симметрии S-0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две стороны равны истинным величинам образующих, а третья хорде, стягивающей дугу окружности основания между соседними точками деления. Построенные на развертке точки 0, 1, 2, . соединяются.

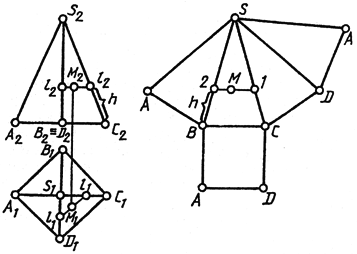
Построение развертки значительно упрощается, если поверхность представлена прямой пирамидой правильной формы или прямым круговым конусом. На рис. 150 приведена развертка четырехгранной прямой пирамиды.

Построение ее упрощается тем, что образующие пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее спроецировались в натуральную величину. Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить стороны AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А соответственно, получим точку В и т. д. Основание же в натуральную величину можно построить на базе одной из его сторон (на рис. 150 — на базе стороны АВ). Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М₂) проведем горизонтальную линию до пересечения с ребрами А₂S₂ и B₂S₂. Получим точки 1₁ и 2₂. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD, на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 1, 2.

На рис. 151 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку.

Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки М₂ проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку М₂. Расстояние от основания конуса до точки М₂ по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки М на развертке.

Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Построение развертки пирамиды способом треугольников

§ 24. Построение разверток поверхностей тел

Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки.

Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике.

Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани. Истинные размеры ребер граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций (проецированием на дополнительную плоскость), приведенными в предыдущем параграфе.

Рассмотрим построение разверток поверхности некоторых простейших тел.

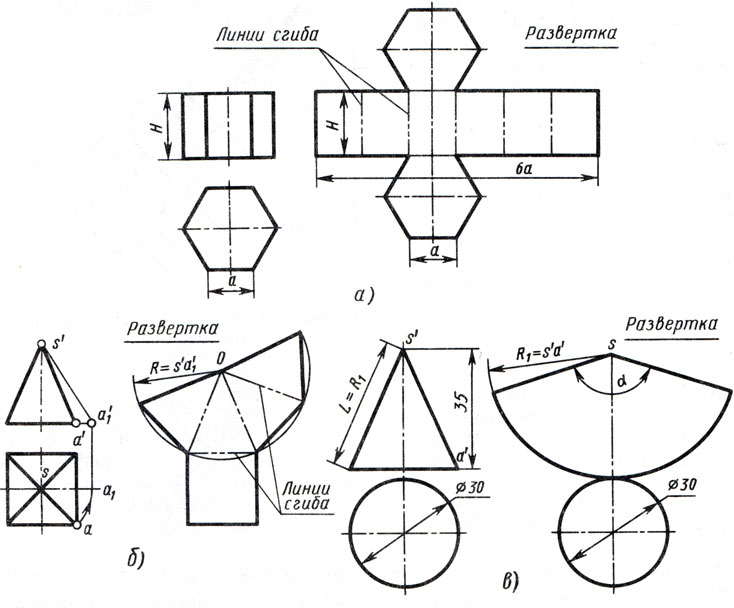
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух равных между собой многоугольников оснований. Для примера взята правильная прямая шестиугольная призма (рис. 176, а). Все боковые грани призмы — прямоугольники, равные между собой по ширине а и высоте Н; основания призмы — правильные шестиугольники со стороной, равной а. Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е. 6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба — штрихпунктирной с двумя точками.

Подобным образом можно построить развертки прямых призм с любой фигурой в основании.

Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней — равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 176, б). Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинают с определения истинной величины наклонного ребра SA. Определив способом вращения (см. рис. 173, в) истинную длину наклонного ребра SA, равную s’a`<sub>1</sub> (рис. 176, б), из произвольной точки О, как из центра, проводят дугу радиусом s’a`₁. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Найденные точки соединяют прямыми с точкой О. Получив развертку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.

Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 176, в). Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, радиусом Rh равным образующей конуса sfd, очерчивают дугу окружности. В данном примере образующая, подсчитанная по теореме Пифагора, равна приблизительно

38 мм (L = √l5 2 + 35 2 = √l450 ≈ % 38 мм). Затем подсчитывают угол сектора по формуле

где R — радиус окружности основания конуса; L — длина образующей боковой поверхности конуса.

В данном примере α = 360°⋅15/38 ≈ 142,2°.

Этот угол строят симметрично относительно осевой линии с вершиной в точке s. К полученному сектору пристраивают круг с центром на осевой линии и диаметром, равным диаметру основания конуса.

Рис. 176. Чертеж разверток поверхностей геометрических тел

Источник

Построение развертки пирамиды способом треугольников

Развертка пирамиды. Как построить развертку шестиугольной пирамиды.

Если вам нужна пошаговая инструкция как построить развертку пирамиды, то прошу к нашему уроку. Первым делом оцените, развернута ли ваша пирамида аналогичным образом, как на рисунке 1.

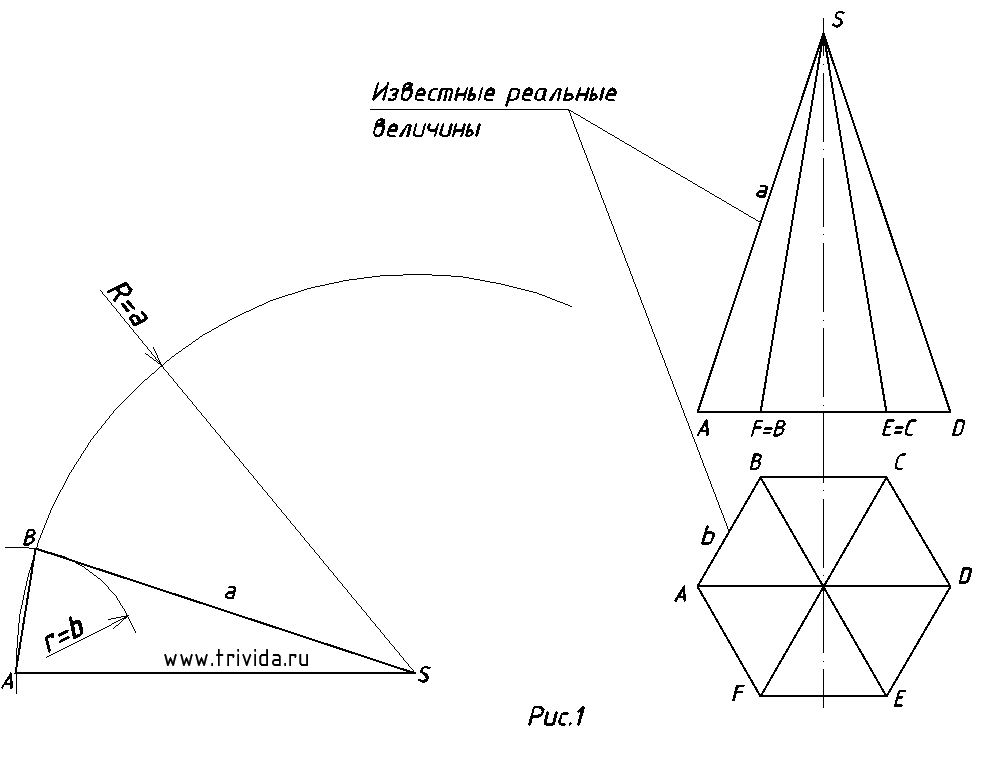
Если у вас она повернута под 90 градусов, то ребро, помеченное на рисунке как «известные реальные величины» в вашем случае можно будет найти на профильной проекции, которую вам необходимо будет построить. В моем же случае этого не требуется, все необходимые для построения величины у нас уже есть. Важно не забыть, что в данном чертеже только ребра SA и SD на фронтальной проекции отображены в натуральную величину. Все остальные проецируются с искажением длины. Кроме того, на виде сверху все стороны шестиугольника так же спроецированы в натуральную величину. Исходя из этого приступим.

1. Для пущей красоты проведем первую линию горизонтально (рисунок 1). Затем, проведем широкую дугу радиусом R=a, т.е. радиусом равным длине бокового ребра пирамиды. Получим точку А. Из нее сделаем с помощью циркуля засечку на дуге, радиусом r=b (длина стороны основания пирамиды). Получим точку B. У нас уже есть первая грань пирамиды!

2. Из точки B сделаем еще одну засечку таким же радиусом — получим точку C и соединив ее с точками B и S получим вторую боковую грань пирамиды (рисунок 2).

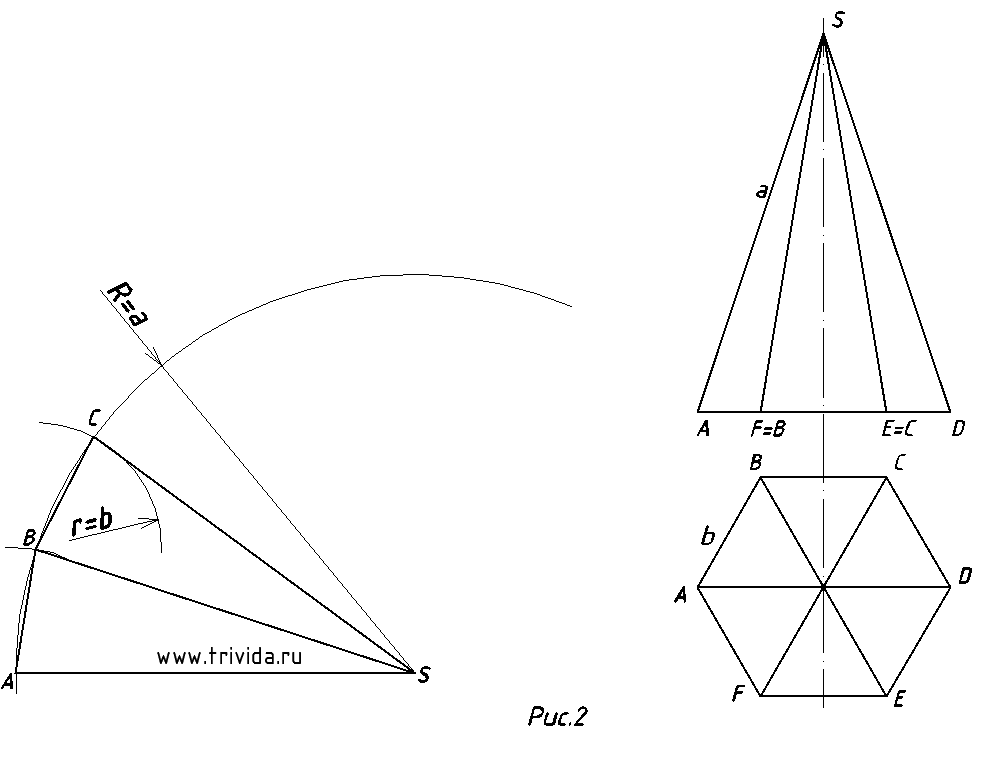
3. Повторив данные действия необходимое количество раз (все зависит от того, сколько граней у вашей пирамиды) мы получим такой вот веер (рисунок 3). При правильном построении вы должны получить все точки основания, причем крайние должны повториться.

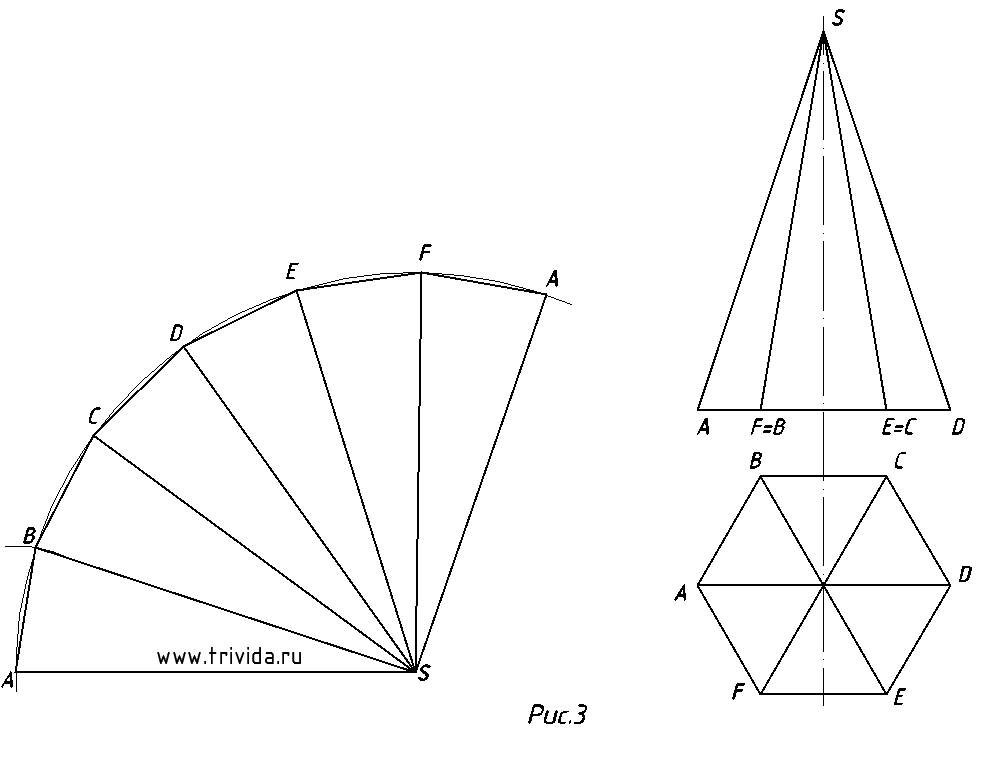
4. Это требуют не всегда, но все же оно нужно: добавить основание пирамиды к развертке боковой поверхности. Начертить шести-восьми-пятиугольник все дочитавшие до этого места, полагаю, умеют (как начертить пятиугольник подробно рассказано в этом уроке) Сложность же заключается в том, что фигуру нужно начертить в нужном месте и под нужным углом. Через середину любой грани проведем ось. Из точки пересечения с прямой основания отложим расстояние m, как показано на рисунке 4.

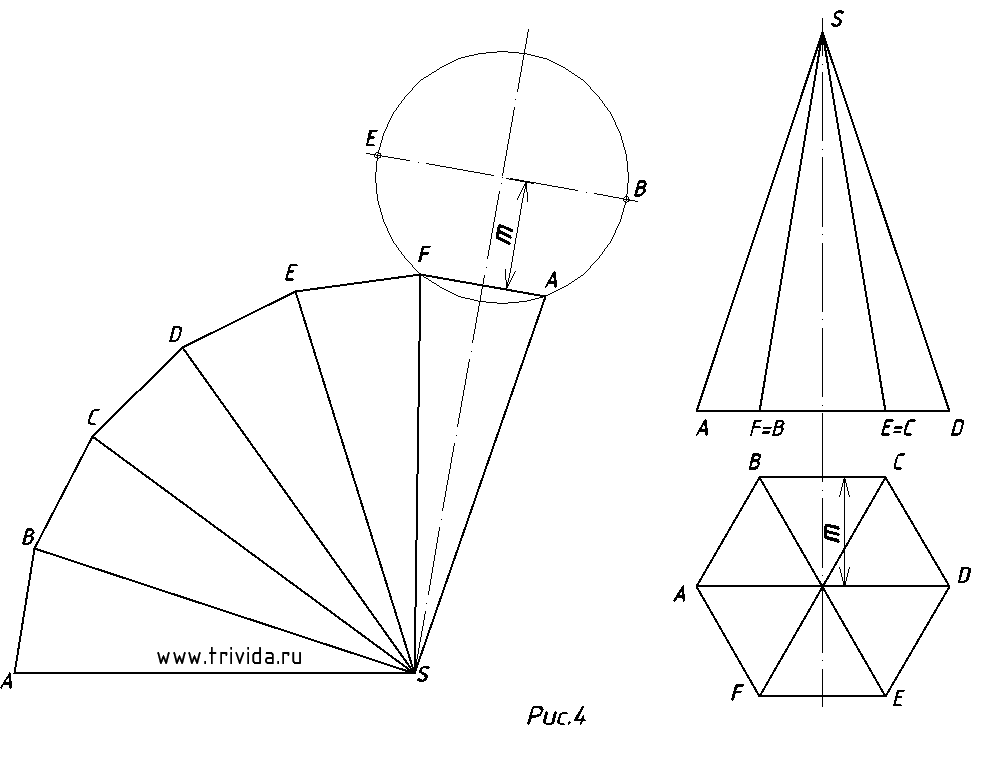
Проведя через эту точку перпендикуляр, мы получим оси будущего шестиугольника. Из полученного центра проводим окружность, как вы поступали при построении вида сверху. Обратите внимание, что окружность должна пройти через две точки боковой грани (в моем случае это F и A)

5. На рисунке 5 показан конечный вид развертки шестиугольной призмы.

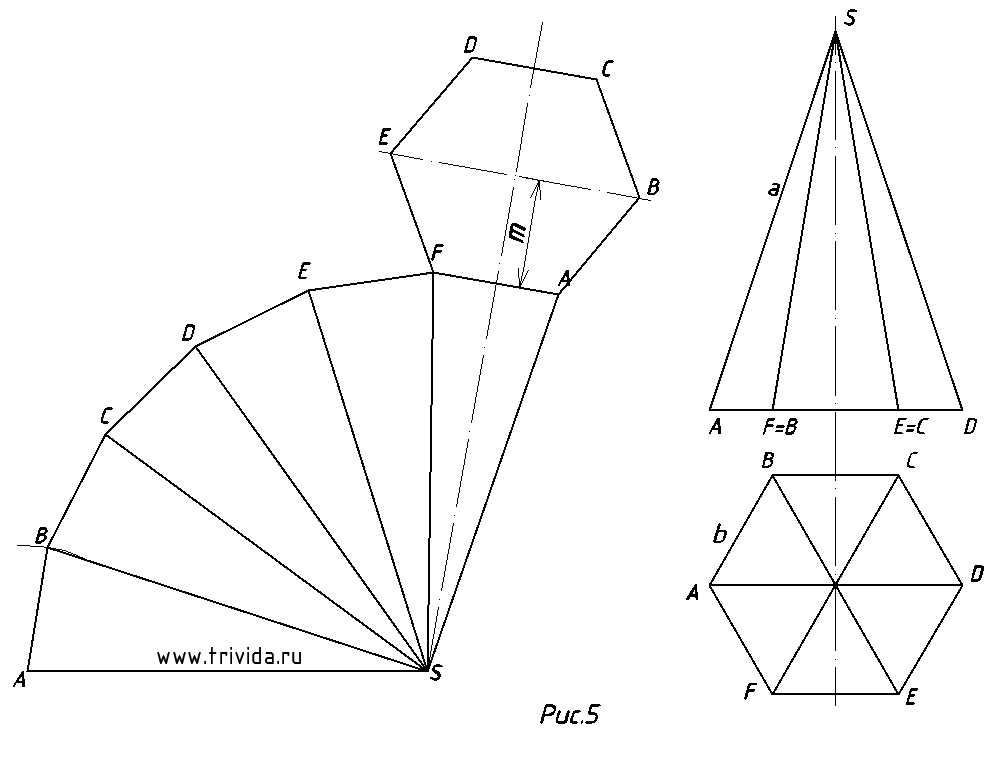
На этом построение развертки пирамиды завершено. Стройте ваши развертки, учитесь находить решения, будьте въедливыми и никогда не опускайте рук. Спасибо, что зашли. Не забудьте порекомендовать нас друзьям 🙂 Всего хорошего!

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Автор комментария: Алина
Дата: 2015-12-24

Ребята, спасибо, выручили! Даже преподаватель так не объясняет! Спасибо огромное!8

Вот спасибо вам, порадовали! Чего-то такого я и ждал все эти годы :))) Пусть все получается!

Автор комментария: Кирилл
Дата: 2016-01-17

спасибо вам большое

Автор комментария: Роман
Дата: 2016-02-03

от души Спасибо!

Автор комментария: Неля
Дата: 2016-02-06

Автор комментария: Лилия
Дата: 2016-12-13

Спасибо автору, выручил очень) Написано коротко и ясно без заморочек)9

Автор комментария: Надежда
Дата: 2018-12-11

Источник