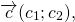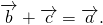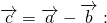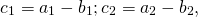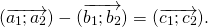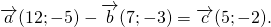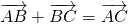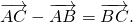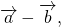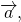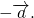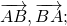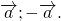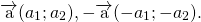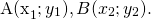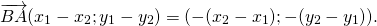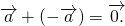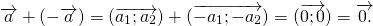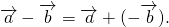- Вычитание векторов. Как найти разность векторов
- Откладывание вектора от данной точки
- Вычитание векторов. Правило первое
- Готовые работы на аналогичную тему
- Вычитание векторов. Правило второе
- Пример задачи на понятие разности векторов
- Разность векторов
- Сложение и вычитание векторов.
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Вычитание векторов. Как найти разность векторов
Вы будете перенаправлены на Автор24
Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Введем следующую теорему:
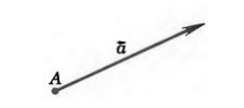
От любой точки $K$ можно отложить вектор $\overrightarrow$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
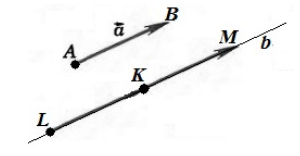
Пусть нам даны векторы $\overrightarrow$ и $\overrightarrow$.
Готовые работы на аналогичную тему
Построение разности двух векторов рассмотрим с помощью задачи.
Решение.
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
Из определения 2, получаем, что
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Вектор $\overrightarrow
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow\right)$, получим
Так как векторы $\overrightarrow$ и $\left(-\overrightarrow\right)$ противоположны, то $\overrightarrow+\left(-\overrightarrow\right)=\overrightarrow<0>$. Имеем
Теорема доказана.
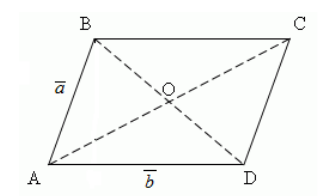
Пример задачи на понятие разности векторов
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
Из первого правила разности двух векторов, получаем
б) Так как $\overrightarrow
По теореме 2, имеем
Используя правило треугольника, окончательно имеем
Источник
Разность векторов
Разность векторов
— это такой вектор
который в сумме с вектором b даёт вектор a:
На основе определения находим координаты вектора
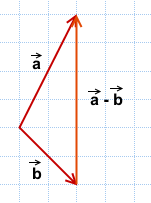
Как построить разность двух векторов?
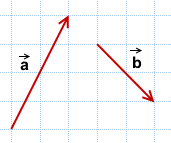
правило построения разности двух векторов
Чтобы построить вектор, равный разности векторов
надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.
Противоположные векторы — это противоположно направленные векторы одинаковой длины.
Вектор, противоположный вектору
Свойства противоположных векторов:
1) Противоположные векторы имеют противоположные координаты:
Пусть даны точки
2) Сумма противоположных векторов равна нулевому вектору:
2 способ построения разности векторов

можно к вектору a прибавить вектор, противоположный вектору b:
То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.
Источник
Сложение и вычитание векторов.
Сложение и вычитание векторов.
Сумма двух векторов. Законы сложения векторов. Правило параллелограмма.
Представим себе такую ситуацию. Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой. Сейчас мы описали принцип первого правила сложения векторов.
Чтобы найти вектор суммы двух векторов и , нужно:
совместить параллельным переносом начало вектора с концом вектора ;
провести вектор из начала вектора в конец вектора ;
получившийся вектор и есть вектор суммы: .
Если к вектору прибавить нулевой вектор по правилу треугольника, то получим вектор , т.е. справедливо равенство: .
Утверждение. Если и – произвольные точки, то .
Сложение векторов подчиняется алгебраическим законам.
ТЕОРЕМА. Для любых векторов и справедливы равенства:
Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны.
1). Отметим произвольную точку и отложим от этой точки вектор . Воспользуемся правилом треугольника и прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок слева).
Теперь от точки и отложим вектор . По правилу треугольника прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок справа).
– параллелограмм и точка совпадает с точкой . Значит, , т.е.
2). От точки отложим вектор , от точки отложим вектор , а от точки – вектор . Найдём суммы векторов по правилу треугольника.
При доказательстве первой формулы получился параллелограмм, причём, из точки выходят два вектора и , а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.
Чтобы найти вектор суммы двух векторов и , нужно:
совместить параллельным переносом начала векторов и ;
на этих векторах достроить параллелограмм;
вектором суммы является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.
Сумма нескольких векторов.
Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример.
Отметим точку и отложим от неё вектор . Прибавим к нему вектор по правилу треугольника. . Теперь к вектору прибавим вектор . . К вектору прибавляем вектор . . Осталось к вектору прибавить вектор . .
Итак, . Значит, суммой векторов является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.
Чтобы найти вектор суммы нескольких векторов, нужно:
последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего;
вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего.
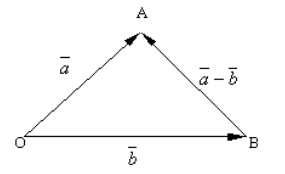
Определение. Разностью двух векторов и называется такой вектор , что при сложении его с вектором получается вектор .
Вычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них.
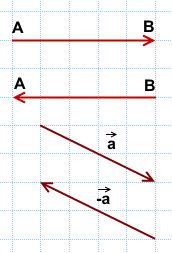
Сложим векторы и по правилу треугольника. По рисунку видно, что . Отсюда, и . Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:
Чтобы найти вектор разности двух векторов, нужно:
совместить параллельным переносом начала этих векторов;
вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора.
Чтобы найти вектор разности двух векторов, нужно:
совместить параллельным переносом концы этих векторов;
вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора.
Далее, из алгебры мы знаем, что для того, чтобы из числа вычесть число , нужно к числу прибавить число, противоположное числу , т.е. . Такое же правило справедливо и для векторов.
ТЕОРЕМА. Для любых векторов справедливо равенство:
1. Найдём разность векторов по I правилу. Вектором разности является вектор (рисунок слева). А теперь найдём сумму векторов по правилу треугольника, где – вектор, противоположный вектору . Вектором суммы является вектор (рисунок справа). Не трудно заметить, что . Они сонаправлены и имеют одинаковые модули.
2. А теперь докажем то же самое аналитически. По определению разности векторов,
Что и требовалось доказать.
Из этой теоремы следует третье правило вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму.
Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно.
Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.
Проведите векторы . Какая геометрическая фигура у вас получилась?
Вектор является разностью векторов и . Определите, какой из четырёх рисунков верный.
Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.
Выразите вектор через векторы , используя рисунок.
Выразите вектор через векторы , используя рисунок.
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
В квадрате проведены диагонали и . Укажите номера верных утверждений.
– параллелограмм. Найдите сумму векторов .
– прямоугольник. Диагонали и пересекаются в точке . Укажите номера верных утверждений.
параллелограмм. Выразите векторы и через векторы и .

– прямоугольник. Выразите векторы и через векторы и .
– параллелограмм. Выразите векторы и через векторы и .
Найдите длины векторов , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
Две стороны прямоугольника равны 20 и 21. Найдите длину суммы векторов и .
Две стороны прямоугольника равны 7 и 24. Найдите длину разности векторов и .
На каждом рисунке найдите длину вектора (размеры клетки 1 х 1).
На каждом рисунке найдите длину суммы векторов и (размеры клетки 1 х 1).
На каждом рисунке найдите длину разности векторов и , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 829 человек из 76 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 296 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 607 человек из 76 регионов
Ищем педагогов в команду «Инфоурок»
Теоретическая часть данной разработки содержит определения, свойства, правила, связанные с геометрическим сложением и вычитанием векторов. К каждому понятию предложен рисунок, разобраны примеры. Практическая часть разработки содержит задания на построение суммы и разности векторов, а также аналитическое определение суммы и разности векторов. Есть задания, встречающиеся на ОГЭ.
Номер материала: ДБ-741821
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минобрнауки разработало концепцию преподавания истории российского казачества
Время чтения: 1 минута
Попова предложила изменить школьную программу по биологии
Время чтения: 1 минута
В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник