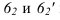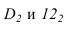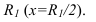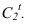Построение падающих теней способом лучевого сечения

3.4. Способ экранов (вспомогательных плоскостей уровня)

Способ экранов применяют для построения падающих теней на поверхность, в сечении которой плоскостями уровня (экранами) получаются геометрически простые линии (окружности или прямые). Например, для построения тени отрезка AB на поверхность вращения применяем горизонтальные экраны, один из которых показан на рис. 3.5.

Тень AB_Т от отрезка, падающая на землю, переходит на тело вращения в точке 1. Тень от отрезка, падающая на экран, параллельна тени AB_Т. В точке 2 эта тень попадает на заданную поверхность. Таки образом, для построения падающей тени от отрезка на поверхность вращения надо провести вспомогательную плоскость уровня (экран) и построить окружность – сечение поверхности этим экраном. Затем строим тень от отрезка на экране. Пересечение этой тени с окружностью дает точку (точку 2 на рис. 3.5), которая находится на искомом контуре падающей тени. Еще один экран – еще одна точка на контуре падающей тени. Так можно построить любое число точек падающей тени. Сколько экранов – столько точек.

На рис. 3.6 показано построение тени на конусе вращения от отрезка AB. Предварительно найдены собственная и падающая тени конуса, а также теньA₁B_1Т отрезка на земле. В точке1 тень от отрезка перемещается с земли на поверхность конуса. Эта точка – начало падающей тени. Точка4 построена с помощью обратного луча, идущего от точки4_1Т пересечения падающих теней конуса и отрезка. Точка4 – последняя точка тени, падающей от отрезкаAB на конус.

Промежуточные точки 2 и3 найдены с помощью экранов. Для построения точки3 использована горизонтальная плоскость уровняΣ, которая пересекает конус по окружности (см. план на рис. 3.6). В точкеR экранΣ пересекается с отрезкомAB. Тень от отрезкаAB на экранеΣ начинается в точкеR, а в точке3 перемещается на конус.

Для поиска очерковой теневой точки 2 использована фронтальная плоскость уровняΔ, пересекающая конус по фронтальному очерку. В точкеC экранΔ пересекается с отрезкомAB. ТеньCT отрезка на экранеΔ пересекается с очерком конуса в искомой очерковой точке2.

3.5. Способ лучевых сечений

Способ основан на двух позиционных задачах начертательной геометрии. Действительно, тень от точки, падающая на любую поверхность – это точка пересечения светового луча с поверхностью. Построение точки пересечения светового луча с поверхностью – первая позиционная задача. Тень от фигуры – это линия пересечения данной поверхности с лучевой поверхностью. Построение линии пересечения поверхностей – вторая позиционная задача. Лучевая поверхность образована световыми лучами, проходящими через контур собственной тени фигуры.

На рис. 3.7 показана тень, падающая от треугольника на конус вращения. Как она найдена? По точкам. Рассмотрим, например, построение тени от точки B. Через вершину B проводим лучевую секущую плоскость Σ, которая пересекает конус по гиперболе (рис. 3.7, а). Точка пересечения светового луча с гиперболой дает тень на конусе от точки B (первая позиционная задача). Для построения гиперболы на конусе начерчены параллели (окружности). Тени от других точек треугольника построены таким же способом (рис. 3.7, б). Следует обратить внимание на секущую лучевую плоскость Δ, проходящую через ось конуса и пересекающую его не по гиперболе, а по двум прямым (поэтому точки 1 и 2 на рис. 3.7, б определяются особенно просто).

При построении тени от шеста, падающей на здание, также использован способ лучевых сечений (рис. 3.8). Лучевая плоскость Σ, проходящая через шест, пересекает стены и крышу здания по ломаной линии 1-2-3-4-5. Тень от вершины A шеста попадает на эту линию.

Источник

Построение падающих теней в начертательной геометрии с примерами

Построение падающих теней на комбинированных поверхностях вращении:

Рассмотрим построение теней на комбинированной поверхности вращения типа «Ваза» (рисунок 12.1). Комбинированная поверхность состоит из тора, цилиндров, сферы, скоции. Для того, чтобы построить, падающие тени, прежде всего необходимо построить собственные тени, так как контур падающей тени, есть тень от контура собственной тени. Построение собственных теней элементов поверхности вазы были рассмотрены в предыдущей лекции №11: тор (рисунок 11.8), цилиндр (рисунок 11.1), сфера (рисунок 11.7), скоция (рисунок 11.9).

Необходимо отметить некоторые закономерности контуров собственных теней:

• — на линии касания двух разных поверхностей контуры собственных теней этих поверхностей имеют точки перелома (точки
• — когда две соосные поверхности имеют общую линию пересечения, то контуры собственных теней не будут иметь общей точки (точки

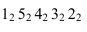
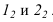
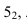
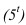
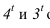
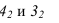
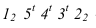
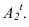
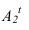
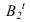
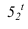
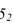
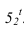
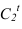
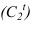
Далее приступаем к построению падающих теней. Тень от контура собственной тени тора падает на освещенную поверхность цилиндра. Для ее построения используется метод вспомогательного осевого экрана. При этом точки лежат на осевом экране. Точка лежащая в лучевой плоскости, отбросит тень на ось . Теньот точек строится методом выноса. Контур — контур тени падающей на фронтальный экран. Пересекая левую образующую цилиндра он дает точку . На одной горизонтали с находим на оси. Высшая точка падающей тени определяется следующим образом. Находится горизонталь пересечения конуса с углом образующей 35° с цилиндром. Луч проведенный из точки под углом 45° с этой горизонталью и дает точку Точку — точку исчезновения тени — определяем обратным лучом, построив тень от образующей цилиндра на фронтальный экран. При этом нужно иметь ввиду, что линия контура падающей тени в точке исчезновения должна быть касательна к проекции луча.

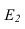
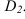
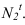
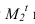
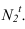
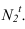
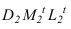
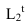
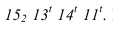
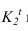
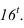
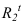
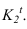
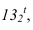
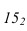
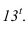
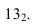
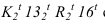
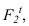
Далее строим тень, падающую от сферы на цилиндр. Тень начинается из точек и Строим тень от сферы на фронтальный экран. Контур тени, пересекая образующую цилиндра, дает точку Точку находим на оси на одной горизонтали с Точку определяем обратным лучом, построив тень образующей цилиндра на фронтальный экран. Нужно обратить внимание на то, что контур падающей тени будет касательным к линии пересечения поверхностей сферы и цилиндра, а в точке касательным к проекции луча. Далее строим тень от нижнего основания цилиндра, падающую на скоцию (тороид). Для этого строим тень от окружности на фронтальный экран — Пересекаясь с контуром скоции, она дает точки и . Точка лежит на одной горизонтали с. Для нахождения высшей точки падающей тени — точку соединяем с Эта прямая является образующей конуса с углом 35°. Строим горизонталь пересечения этого конуса с поверхностью скоции и находим на ней точку пересечения луча проведенного из точки Соединяем полученные точки с таким расчетом, чтобы в точке исчезновения тени контур тени касался проекции луча.

Метод биссекторного экрана

В некоторых случаях для построения падающих теней на поверхностях вращения удобно использовать вспомогательный биссекторный экран. Эта биссекторная плоскость удобна тем, что тень на нее от горизонтальной окружное™ проецируется также окружностью радиуса 0,707 данной. Способ биссекторных экранов применяется в сочетании со способом обратных лучей.

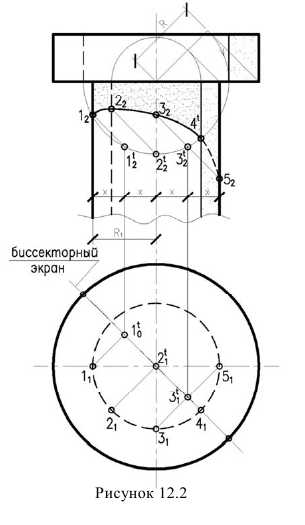
Для примера рассмотрим построения тени от круглой плиты на круглую колонну (рисунок 12.2).

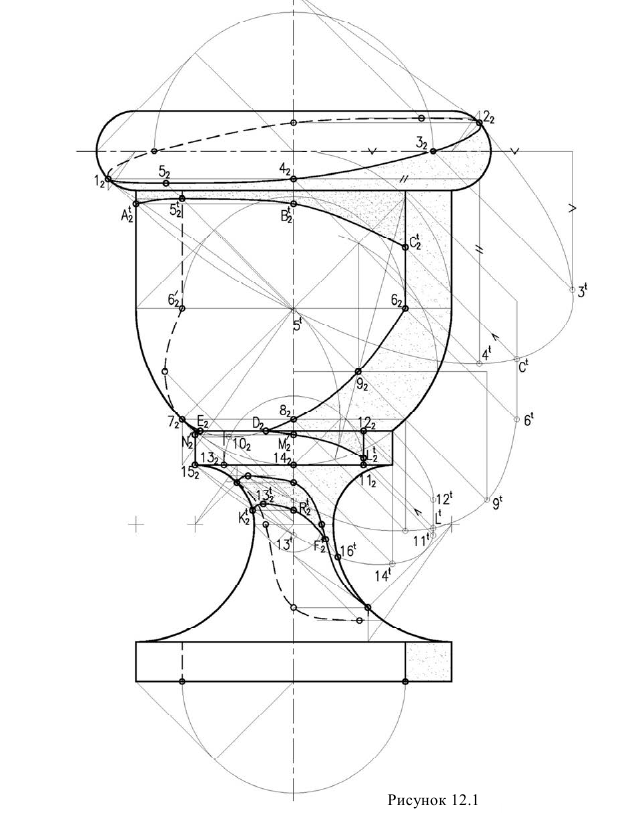
Тень от окружности плиты на биссекторный экран — окружность радиуса R. Тень от левой контурной образующей колонны падает на середину левого радиуса цилиндра

Тень от бликовой образующей колонны 2 надает на ось цилиндра.

Тень от средней образующей 3 падает на середину правого радиуса цилиндра.

Тень образующей 5 совпадает с тенью образующей 3 при обратном луче.

Находим точки пересечения теней образующих, падающих на биссекторный экран, с тенью от плиты и обратными лучами, определяем их положения на соответствующих образующих.

На рисунке 12.2 горизонтальная проекция дана только для пояснения построений. Фактически построения могут быть выполнены только по фронтальной проекции.

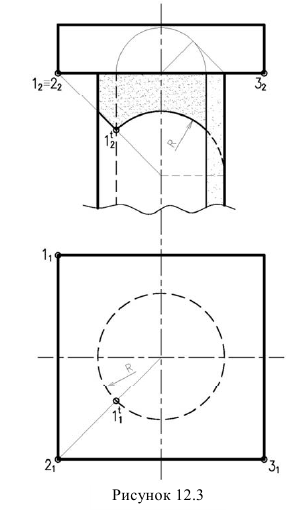
Тень от квадратной плиты на колонну:

Тень от квадратной плиты на цилиндрическую колонну (рисунок 12.3) фактически является тенью от двух прямых 1-2 — фронтально-проецирующей и 2-3 — профильно-проецирующей (по отношению к фасаду -продольной).

Нам из предыдущего материала известно, что тень от продольной прямой зеркально повторяется план, т.е. является окружностью того же радиуса, что и колонна. А тень от проецирующей прямой совпадает с направлением луча. Поэтому очевидно, что построение тени можно выполнить по одной фронтальной проекции, т.е. фасаду.

Построение падающих теней на архитектурных деталях:

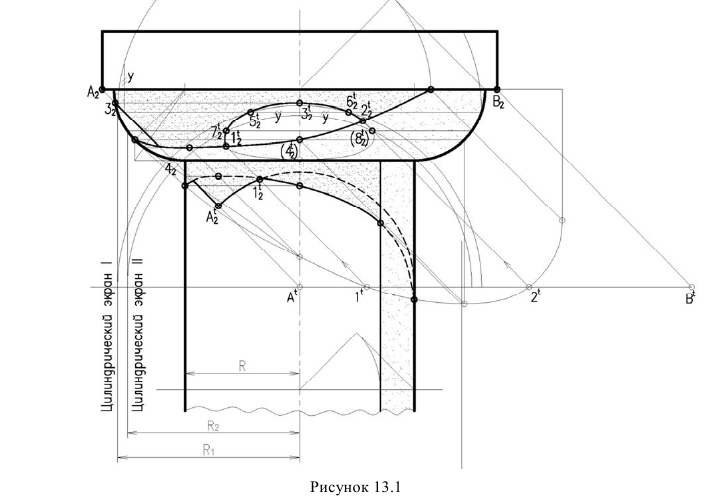
Тени канители колоны

Построение тени капители (рисунок 13.1) представляет собой комплексную задачу, объединяющую ранее построенные тени на отдельных частях. Собственные тени на цилиндре и на валике (тор), падающая тень от валика на колонну (цилиндр) выполнена аналогично рисунку 12.1. А построение падающей тени от квадратной плиты на валик строится способом цилиндрических экранов или глубинных координат. Сначала построим тень, от квадратной плиты падающую на колонну. Построение выполняется аналогично рисунку 12.3. В итоге, контур падающей тени на цилиндрической колонне, складывается из тени падающей от валика и квадратной плиты. Тень от продольной стороны квадрата представляет окружности радиуса R. Тень от проецирующей стороны квадрата совпадает с направлением луча, как на колоне, так и на валике. Необходимо построить тень от продольной стороны квадрата на валик. 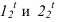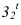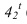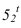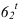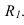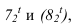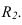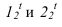Точки — точки исчезновения тени находим обратным лучом с фронтального осевого экрана. Высшую точку и низшую — (мнимую) находим на параллелях проведенных из точек пересечения тени от проецирующей стороны квадрата на валике. Для построения промежуточных точек контура тени применяем вспомогательные цилиндрические экраны. Теневые точки и находим на линии пересечения цилиндрического экрана I с валиком, построив тень как на цилиндре радиуса . Аналогично строим теневые точкиприменив цилиндрический экран II радиусаПолученные точки соединяем плавной кривой, учитывая, что в точках лучи будут касательными к полученной кривой.

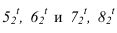
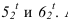
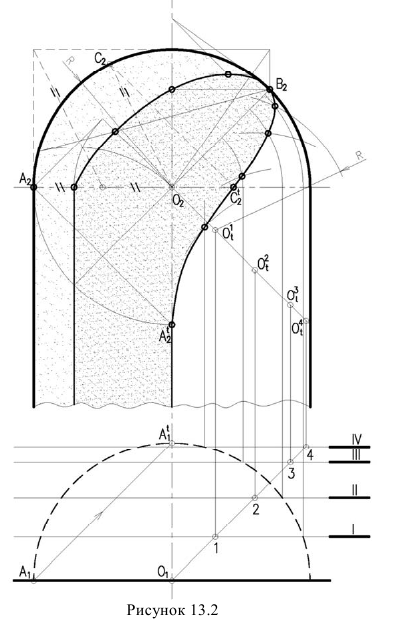
Промежуточные точки можно также получить способом глубинных координат. Для этого берется ряд горизонтальных сечений. На примере сечение показано совпадающим с основанием цилиндрического экрана I. Для дальнейшего построения окружность сечения совмещается с фронтальной плоскостью. Определяется координата у, которая откладывается на линии сечения в обе стороны от оси для получения точек Аналогично строятся другие точки.

Тени в цилиндрической нише со сферическим верхом (рисунок 13.2)

Прежде всего определяем контур собственной тени известными способами (рисунки 11.1, 11.7) Для построения падающей тени в данной комбинированной нише применяется метод фронтальных экранов. Суть метода заключается в том, что тень от окружности на плоскость ей параллельную является окружностью. Тень от контурной образующей цилиндра, а, следовательно, и от точки А падает на ось цилиндра. 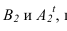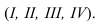Необходимо определить промежуточные точки между , принадлежащие контуру падающей тени от кромки сферической ниши — окружности. Для этого проводим ряд фронтальных экранов Строим линии пересечения фронтальных плоскостей (экранов) с поверхностью ниши. Определяем положение теней от центра окружности кромки ниши О на каждый из экранов. Из теней центров окружности выполняем засечки на соответствующих линиях сечения, радиусом сферы R.

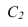
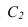
Точка перегиба тени С, на окружности перехода поверхности цилиндра в поверхность сферы, может быть определена следующим образом. Из центра О проводим прямую с уклоном 2:1, которая определит положение точки на кромке сферической ниши. Луч проведенный из точки даст тень

Полученные точки соединяем плавной кривой линией.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Проекции с числовыми отметкам
• Гранные поверхности
• Проецирование точки
• Прямая в пространстве и ее изображение на чертеже
• Пересечения криволинейных поверхностей
• Пересечения поверхностей с прямой и плоскостью
• Взаимное пересечение поверхностей
• Собственные тени поверхностей вращения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник