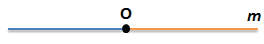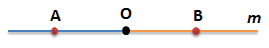Построение луча все способы

Что такое луч в математике

Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.

Луч — геометрическое понятие

Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.

На картинке вы можете посмотреть, что такое луч и как он выглядит:

Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.

Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.

Отличия луча от прямой и от отрезка

В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.

В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.

В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.

Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:

• отрезок имеет начальную и конечную точки;
• луч — только начало;
• прямая — не располагает начальной и конечной точками.

Взаимное расположение лучей

Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.

На рисунке начало для лучей — общая точка A.

По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.

Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.

Дополнительные лучи — это фигуры, которые обладают такими признаками, как:

• имеют совпадающее начало в одной точке;
• располагаются на одной прямой линии;
• направляются в разные стороны, то есть угол между ними составляет 180 градусов.

Можно ли сравнить два луча?

Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.

Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.

Луч — альтернативные значения слова

Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.

Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.

Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:

В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.

Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.

Источник

Построение луча все способы

Построим прямую АВ

(прямая обозначена двумя большими латинскими буквами, например, А и В)

Отметим на прямой АВ точку О

Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)

Части, на которые точка О разбивает прямую АВ, выделены цветом

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча

Назовем получившиеся лучи:

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет

Луч является геометрической фигурой

Луч — это часть прямой, ограниченная с одной стороны

Луч имеет начало, но не имеет конца

Другой способ обозначений

Построим прямую m

(прямая обозначена малой латинской буквой, например, m)

Точка О разбивает прямую m на два луча

Чтобы лучи обозначить, отметим на прямой m дополнительно произвольным образом две точки — А и В

Назовем получившиеся лучи

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет; точка А принадлежит лучу ОА;

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет; точка В принадлежит лучу ОВ;

Варианты обозначения лучей

1)

Луч ОВ (обозначение двумя большими латинскими буквами)

Точка О — начало луча; В — любая точка на луче ОВ (точка не отмечена)

2)

Луч ОВ (обозначение двумя большими латинскими буквами)

Точка О — начало луча; В — произвольная точка на луче ОВ (точка отмечена)

3)

Луч k (обозначение малой латинской буквой)

Начало луча обозначено буквой О

4)

Луч k (обозначение малой латинской буквой)

Начало луча не обозначено буквой (только отмечено точкой)

Дополнительные лучи

Лучи ОА и ОВ принадлежат одной прямой АВ

Лучи ОА и ОВ имеют общее начало (точка О)

Лучи ОА и ОВ противоположно направлены

При таких условиях лучи ОА и ОВ называются дополнительными

Поделись с друзьями в социальных сетях:

Источник

4 правила построения хода лучей в оптической системе

4 ПРАВИЛА ПОСТРОЕНИЯ ХОДА ЛУЧЕЙ В ОПТИЧЕСКОЙ СИСТЕМЕ

Луч, идущий параллельно оптической оси после линзы пройдет через точку заднего фокуса.

Если параллельный пучок лучей после линзы собирается в одну точку, то такая линза — собирающая, положительная, и точка — ее действительный фокус.

Если параллельный пучок лучей после линзы расходится, как будто все лучи пущены из единого центра, то линза — рассеивающая, отрицательная.

Для понимания, с каким из фокусов имеем дело, принято называть фокус в пространстве предметов — передним, фокус в пространстве изображений — задним.
Фокальные отрезки называются соответственно. Фокальная плоскость — плоскость, проходящая через точку фокуса перпендикулярно оптической оси.

Луч, проходящий через точку переднего фокуса, после линзы пойдет параллельно оптической оси.

Лучи, идущие параллельно друг другу, сойдутся в одной точке на задней фокальной плоскости.

Лучи, идущие из одной точки на передней фокальной плоскости, пойдут после линзы параллельно друг другу.

В пучке лучей выбирается луч, построение которого легко осущетвить, и остальные строятся параллельно ему (выбран луч параллельный оси — зеленый).

Частный случай: Для системы, находящейся в однородной среде — луч, проходящий через центр линзы не преломляется (см. сиреневый луч на рисунке).

Задача построения хода луча

Достаточно одного луча, но существует два способа построения.

Первый способ построения луча

1 Проводим луч параллельно заданному лучу через точку переднего фокуса. Преломленный луч пойдет параллельно оптической оси.
2 Вспомним правило — о лучах, идущих параллельно друг другу.
3 Соединяем точку пересечения луча с задней фокальной плоскостью с точкой выхода заданного луча из линзы. Это и будет искомый луч.

Второй способ построения луча

Основан на том же правиле, но действует от обратного.
1 Находим точку пересечения заданного луча с передней фокальной плоскостью.
2 Через эту точку проводим вспомогательный луч 1 параллельно оптической оси. Преломленный луч 1′ как пойдет? — через точку заднего фокуса.
3 По правилу, такие лучи (исходящие из одной точки) как пойдут? — параллельно друг другу. Из точки пересечения заданного луча с линзой строим преломленный луч параллельно лучу 1′.

Примеры решения задач

Построение сложного изображения

Решение задач на построение сложного изображения сводится к более простой задаче и решается традиционным способом. Предмет, состоящий из нескольких точек строится как результат построения данных точек на предмете.

Задачи

1 Построить изображение предмета. Положительная линза.

Решение

1 Сначала строим изображение нижней точки предмета розовыми лучами.

2 Затем — изображения второй точки синими лучами.

3 Соединяя эти точки, получаем изображение предмета.

2 Построить изображение предмета. Положительная линза.

Решение

1 Сначала строим изображение верхней точки предмета синими лучами. Как и положено для рассеивающей линзы, пересекаться будут не сами лучи, а их продолжения.

2 Затем строим изображение второй точки зелеными лучами.

3 Соединяя эти точки, получаем изображение предмета.

Построение предмета по заданному изображению

Построение предмета по изображению сводится к решению обратной задачи. Суть та же, что и в построении изображения.

Необходимы 2 луча, идущие через точку изображения. Пересечение этих лучей в пространстве предметов, даст нам точку предмета.

Проводим луч через край изображения параллельно оптической оси. Преломленный луч пройдет через точку переднего фокуса. Проведем луч через край изображения и точку заднего фокуса. В пространстве предметов луч пойдет параллельно оптической оси. На пересечении построенных лучей находится искомое изображение точки предмета.

Положительная линза (построение предмета для действительного изображения)

Положительная линза (построение предмета для мнимого изображения)

Отрицательная линза

Определение положения кардинальных точек и плоскостей системы

Решение задач этого типа основано на том, что среда однородная. Поэтому правомерно проводить луч через центр линзы. Этот луч пойдет после системы под тем же углом, что и до системы. Угловое увеличение равно единице.

3.Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение

Для построения необходимо воспользоваться уже знакомым правилом: лучи, идущие параллельно друг другу, сойдутся в одной точке на задней фокальной плоскости.

Последовательность построения:

Но на рисунке показано получение и передней и задней фокальных плоскостей с помощью построения:

4 Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение

Строим синий луч, параллельный заданному в пространстве предметов.

Находим точку пересечения этого луча с заданным в пространстве изображений. Как видно из рисунка, пересекутся лишь продолжения лучей, что говорит о рассеивающем характере системы.

Через точку пересечения проходит задняя фокальная плоскость.

Поиск передней фокальной плоскости основан на том же принципе

В пространстве изображений строим через центр линзы зеленый луч, параллельный заданному. В постранстве предметов этот луч пойдет под тем же углом и пересечет заданный луч в плоскости переднего фокуса системы. Найдя пересечение лучей, находим передний фокус.

Задачи для самостоятельной работы

Примеры решения задач на построение хода лучей и/или изображения были подробно рассмотрены в предыдущих параграфах.

Задачи для домашних работ

1 Построить изображение:

2 Найти предмет:

3 Достроить луч:

4 Построить изображение заданного предмета:

5 Дано изображение. Найти предмет.

6 Достроить луч в пространстве предметов:

7 Построить ход луча:

8 Построить изображение:

9 Построить изображение:

10 Построить ход луча:

11 Достроить ход луча в пространстве предметов и изображений:

12 Достроить ход луча в пространстве предметов и изображений:

13 Задано промежуточное изображение (между первой и второй линзами). Построить сопряженные с ним объекты (в пространстве предметов и изображений):

14 Построить ход луча:

15 Построить изображение заданного предмета:

16 Построить предмет, дающий изображение, показанное на рисунке:

17 Построить изображение:

18 Построить изображение:

19 Построить изображение предмета, показанного на рисунке:

20 Построить изображение:

21 Определить положение фокальных плоскостей для линзы, находящейся в однородной среде:

22 Определить положение фокальных плоскостей для линзы, находящейся
в однородной среде:

23 Определить положение фокальных плоскостей для линзы, находящейся
в однородной среде:

24 Определить положение фокальных плоскостей для линзы, находящейся
в однородной среде:

25 Составить и решить задачу построения хода луча в системе из трех элементов.
Требования к системе:
1 Среди элементов должны быть и положительные и отрицательные.
2 Фокальные плоскости элементов не должны совпадать
3 Обозначение элементов — главными и фокальными плоскостями
Требования к задаче:
1 Исходный луч не должен идти параллельно оси
2 Исходный луч не должен идти через передний фокус первого элемента

26 Составить и решить задачу построения изображения в системе из трех элементов.
Требования к системе:
1 Среди элементов должны быть и положительные и отрицательные.
2 Фокальные плоскости элементов не должны совпадать
3 Обозначение элементов — главными и фокальными плоскостями

Источник