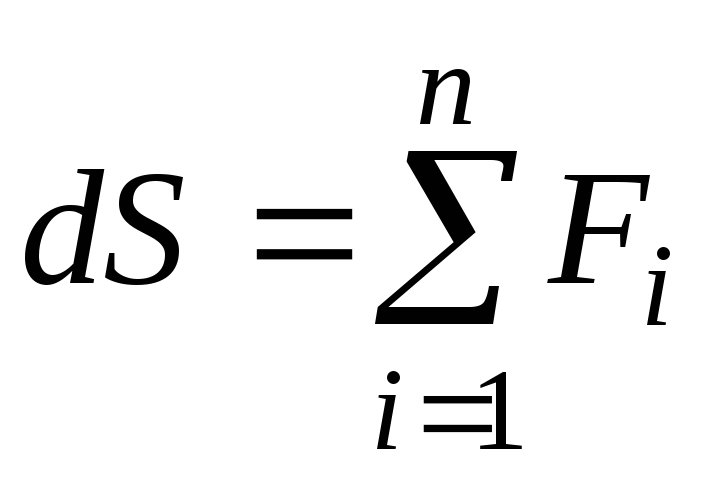Построение линий влияния кинематическим способом

Строительная механика

Главное меню

Присоединяйтесь

Кинематический метод построения линий влияния

Кинематический способ построения линий влияния для внутренних усилий базируется на принципе возможных перемещений Лагранжа. Суть данного принципа заключается в том, что для системы, находящейся в состоянии равновесия, сумма работ всех действующих сил на возможных малых перемещениях равна нулю.

Для построения линии влияния реакции, поперечной силы или изгибающего момента для заданного сечения балки необходимо удалить связь, линию влияния внутреннего усилия для которой требуется построить, и вместо нее ввести требуемое усилие. Таким образом, заданная система станет механизмом с одной степенью свободы. В направлении рассматриваемого внутреннего усилия вводится бесконечно малое перемещение. Направление этого перемещения должно совпадать с внутренним усилием , чтобы оно совершала положительную работу. На базе принципа возможных перемещений записывается уравнение равновесия, из решения которого и определяется требуемое усилие.

Пример: построим линию влияния поперечной силы в сечении k (рис. 1, а). Для этого требуется построить эпюру перемещений балки от единичного смещения по направлению исключенной связи, как показано на рис. 1, б.

Рисунок 1. Линия влияния поперечной силы

В рассматриваемом сечении вводится шарнирно подвижная связь и балке в месте приложения этой связи вводится бесконечно малое линейное перемещение δ_k.

Записываем условие равновесия по принципу Лагранжа (знак «+» при совпадении направления силы и перемещения) :

Поскольку в полученном уравнении знаменатель является числом постоянным (задавалось в начале), то эпюру перемещений балки от единичного смещения по направлению требуемого усилия можно считать линией влияния этого усилия. Кинематический способ построения линий влияния чаще всего используется для построения моделей линий влияния усилий, что позволяют решить задачу об опасном загружении многопролетной балки временной нагрузкой при определении экстремальных усилий.

Источник

Построение линий влияния многопролетных балок кинематическим способом

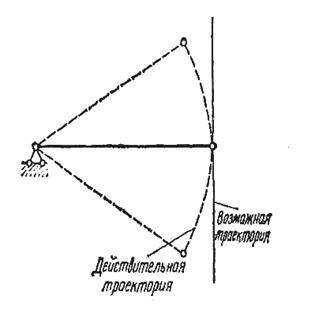
Построение линий влияния кинематическим методом основано на использовании принципа возможных перемещений, изучаемого в курсе теоретической механики. Возможные перемещения — бесконечно малые перемещения, допускаемые связями. Возможные перемещения направлены по касательной к действительной траектории (рис.3.25).

Рис. 3.25. Схема, показывающая принцип возможных перемещений

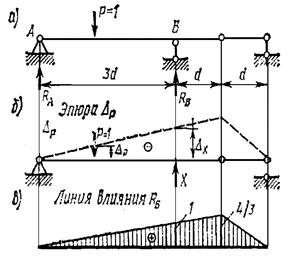
Для построения линии влияния опорной реакции надо отбросить связь, линию влияния усилия в которой необходимо построить, заменив ее действие силой X (рис.3.26 б). Задать полученному механизму возможное перемещение таким образом, чтобы эпюра перемещений совпала с положительным направлением линии влияния у рассматриваемой опоры (рис.3.26 б).

Рис. 3.26. Схема для построения линии влияния опорной реакции R_B кинематическим методом

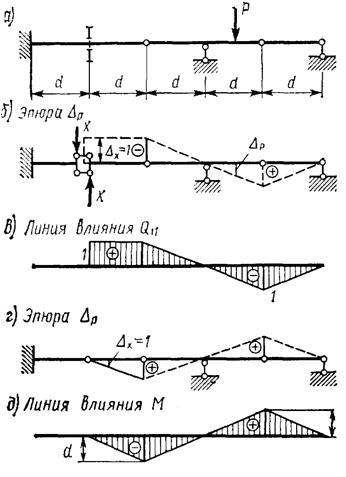
Для построения линии влияния изгибающего момента в каком либо сечении необходимо врезать в это сечение шарнир и моментную связь заменить моментом X и дать возможность перемещения получившемуся кинематическому механизму (рис.3.27 г, д). Для построения линии влияния поперечной силы в каком либо сечении балки надо врезать в это сечение шарнирный параллелограмм, приложить условные силы X (рис.3.27 б) и дать перемещение кинематическому механизму. Полученная таким образом эпюра перемещений совпадает с линией влияния поперечной силы (рис.3.27 в).

Рис. 3.27. Схема для построения линий влияния изгибающего момента М и поперечной силы Q в сечении I-I кинематическим методом

Источник

2.7. Кинематический способ построения линий влияния

Кинематический способ построения линий влияния основан на принципе возможных перемещений (принцип Лагранжа). Если система твёрдых тел, связанная между собой идеальными связями, находится в равновесии, то сумма работ всех заданных сил на любых сколь угодно малых возможных перемещениях равна нулю.

Идеальными считаются такие связи, в которых отсутствуют трение, обмятия узлов и другие аналогичные явления. Возможными считаются такие перемещения, какие допускают идеальные связи.

В соответствии с этим методом каждая линия влияния представляет собой эпюру перемещений. Рассмотрим построение линии влияния опорной реакции (рис. 2.15) для однопролётной балки АВ.Поместив подвижную единичную силуFв произвольную точку, отбрасывают опорную связь в точкеА.

Под действием силы F=1балка АВ,ставшая механизмом, повернётся вокруг опорыВна угол,а перемещение точки под силой F=1составит величину у.

В соответствии с принципом Лагранжа можно записать следующее выражение:

абота силы взята со знаком минус, так как силаR_Aпротивоположна направлению перемещения точки А.Учитывая то, что F =1,из (2.9) найдёмR_A= 1у.

Если ординаты возможных перемещений выразить как функцию угловой скорости возможного вращения вокруг шарнира В,то выражение величины опорной реакции получит такой же вид, как и выражение (2.1),

т. е. R_A=F. Исходя из это- го, когда подвижная силаF =1 будет находиться над опоройА,

станет соблюдаться равенство у=.

При построении линии влияния момента для превращения балки АВв механизм (рис. 2.16) в сечение, для которого требуется построить эту линию влияния, вводят условный шарнир. Высвободившееся усилие обозначают символомM. Введение шарнира даёт балке возможность провиснуть, и эпюра возможных перемещений такой балки охарактеризуется двумя прямыми, взаимно пересекающимися на вертикали под шарниром. Восстановление равновесия может быть достигнуто приложением в рассматриваемом сечении двух равных взаимно противоположных моментовМ.

Выражение возможной работы в этом случае примет следующий вид:

Учитывая то, что F=1,из (2.10) найдёмМ= .

Величины угловых смещений и по их малости могут быть заменены тангенсами, а именнока,тогда последнее выражение примет вид:

М = .(2.11)

По выражению (2.11) можно найти ординаты линии влияния М.

При построении линии влияния поперечной силы Qдля превращения балкиАВв механизм (рис. 2.17) в сечение, в котором требуется построить эту линию влияния, вводят условное устройство, допускающее только взаимный сдвиг звеньев балки между собой.

Выражение возможной работы в этом случае примет вид

Откуда с учётом того, что с+с ′ =, находят

Q = . (2.12)

2.8. Определение расчётного положения

подвижной системы нагрузок

Расчётное положение подвижной системы сосредоточенных сил над линией влияния усилия Sсоответствует maxили minискомой величины этого усилия. В общем случае искомое усилиеSможет иметь несколько экстремальных (maxили min)значений.

В тех случаях, когда искомое усилиеS=f(x),представляет собой функцию положения системы сил на балке, и её первая производная, являющаяся непрерывной функцией, из условияdS/dx = 0можно найти положение подвижной системы сосредоточенных сил, при которых S=f(x)достигает экстремального значения.

Рассмотрим определение экстремального значения усилия Sпри загружении треугольных линий влияния.

Для случая, когда вершина треугольника линии влияния находится в начале или в конце линии влияния (рис. 2.18), экстремальным положение подвижной системы сосредоточенных нагрузок будет тогда, когда вся наибольшая нагрузка находится над вершиной линии влияния или вся система нагрузок находится над всей линией влияния, начиная с её вершины.

То или иное расположение нагрузки зависит от количественных значений каждой из нагрузок, составляющих данную подвижную систему.

В случае, когда подвижная нагрузка представляет собой равномерно распределённую нагрузку, экстремальным будет такое (рис. 2.19) расположение этой нагрузки, когда ординаты этой линии влияния, находящиеся в начале и конце действия распределённой нагрузки у_ни у_к,будут равны между собой.

При загружении треугольной линии влияния системой сосредоточенных подвижных сил (рис. 2.20), когда вершина линии влияния находится на некотором расстоянии аот её начала, любое усилие можно найти исходя из выражения

.(2.13)

Если предположить, что вся система нагрузок сдвинулась вправо или влево, значение усилия получит приращение dS.В правой части равенства (2.13) ординаты изменятся на величинуdxtg_k.Тогда

tg_idx.(2.14)

Сумма, стоящая в правой части равенства (2.14), представляет собой значение первой производной от величины .Известно, что функция достигает своего экстремального значения, когда её первая производная равна нолю. В соответствии с этим

tg_i = 0.(2.15)

Но так как углы наклона ₁, ₂, …, _k, …, _n линии влияния остаются без изменения, выражение (2.15) может обратиться в ноль при условии, если изменяются величины некоторых силF.Последнее условие возможно только при переходе какой-либо силы, называемойF_кр,через вершину линии влияния. Исходя из этого получены условия (2.16), определяющие экстремальное положение над треугольной линией влияния системы сосредоточенных подвижных нагрузок:

(2.16)

В практике расчёта конструкций транспортных сооружений часто используют так называемую эквивалентную нагрузку. Эквивалентной называется такая равномерно распределённая нагрузка интенсивностью q_э, которая создаёт в рассматриваемом сечении такое же усилие, какое вызывает система из сосредоточенных нагрузок, установленная в экстремальном положении.

При загружении линии влияния любого усилия системой сосредоточенных нагрузок усилие может быть найдено по выражению (2.6) .По данному определению эквивалентной нагрузки усилие в соответствии с (2.7) может быть найдено по выражению .Приравнивая оба значения S,найдём

.(2.17)

Очевидно, что величина эквивалентной нагрузки зависит от вида и очертания линии влияния. Однако для подобных между собой линий влияния, которые могут быть построены одна из другой изменением всех ординат в одном и том же соотношении, эквивалентные нагрузки имеют одинаковую интенсивность

Источник

Кинематический способ построения линий влияния

Кинематический способ построения линий влияния

• Кинематический Способ построения влиятельной линии Статический метод построения линии влияния основан на принципе возможного смещения, в зависимости от объема работ, которые на нее воздействуют, поэтому для системы, находящейся в равновесном состоянии.、 В любой статически определимой геометрически

неизменной системе степени свободы равны нулю и не допускают движения ее элементов. Таким образом, такая система преобразуется в переменную (механизм с определенной степенью свободы) путем снятия определенной связи, в которой сила рассматривается в ее направлении. Механизм результирующей движущей силы F —

=1 прикладывается к исследуемой силе, механизм которой сообщается Людмила Фирмаль

как можно более бесконечно малыми движениями. На основе принципа возможных перемещений создается равновесное состояние механизма,которое определяется из решения уравнений, полученных неизвестной силой. Рассматриваемая конструкция линий влияния кинематически поддерживает реакцию, изгибающий момент и боковую силу в одной пролетной балке. Линия влияния опорной

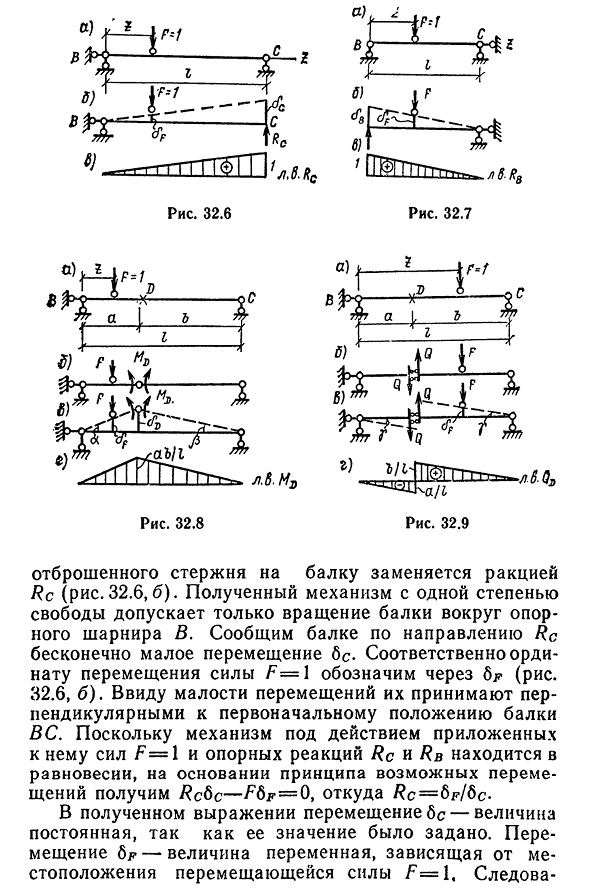
реакции Rc-определить опорную реакцию Rc от движущей силы F=l в пучке BC(рис. 32.6, а) эта реакция возникает при удалении правого опорного стержня. Влияние £ 370 h-g-gttp TSH T Рис 32,7 Шесть. Рис 32,6 qfo Jrv & lL Для других целей см. » l.^ Рис 32.8 Рис. 32.9 Отброшенный стержень на балке заменяется на Rc-секцию (рис.32.6, б). Скажем, Луч в направлении Rc микро движется в направлении BS-соответственно, вертикальная ось движения силы F-1 показана(рис. 32.6, б). Из-за

• малости их перемещений они берутся перпендикулярно к исходному положению балочной пары. Поскольку механизм под действием приложенной к нему силы равен F=l, а опорные реакции Rc и Rb находятся в равновесии, необходимо рассчитать Rc8c-FdF=0 исходя из принципа возможного смещения. В полученной формуле смещение БС является постоянной величиной, так как ее значение задано. Смещение BR-переменная величина, зависящая от положения

движущей силы F=l, Следова- Двадцать четыре* 371 значение эталонной реакции/? Людмила Фирмаль

заданном пучке BC(рис. 32.7, а) эта реакция возникает при удалении левого опорного стержня(рис. 32.7, б). Его воздействие на пучок заменяется реакцией RB. Если сказать лучу бесконечно малое направление движения BV RB, то равновесное состояние механизма под действием приложенной к нему силы F=1 и опорная реакция RB равна RB8B-F8f=0 при BG=0/?b=0; 8F=8B RB=1. Также линия влияния эталонной реакции Rn показана на рисунке. 32.7, ст. Линия влияния изгибающего момента в сечении D. Линии, на которые влияет изгибающий момент, могут быть включены в D-член. 32.8, а) в этой секции шарнир является входным, т. е. из трех связей, соответствующих жесткому соединению балки, один

интерференционный поворот в этой секции снимается,остальные два соединения эквивалентны цилиндрическим шарнирам. Удаленные коммуникации сменяются положительными противоположными моментами. 32.8, 6). Полученный механизм допускает вращение диска BD вокруг опорного шарнира B и вращение диска DC вокруг опоры C. назовем минимальное вертикальное перемещение 8D шарниров-график возможного перемещения механизма показан на рисунке. Исходя из принципа возможных перемещений, записывается представление суммы силы f=1 и момента MD:MDa+MD p-F8f=O, 372 из любого места Поскольку углы поворота диска BD и DC бесконечно малы, их значения заменяются соответствующими

касательными: a=b o/a, 0=6ol>и a+0=6o (A4 -&)/AI-это касательные линии. Итак, 6j?=0AfD=O; 6F = 6D MD = abll. Линия влияния изгибающего момента показана на рисунке. 32,8 г Боковая линия силовых воздействий, в разделе D построить боковую линию силового воздействия в раздел D(фиг. 32.9, а) из него удаляется одно из трех внутренних соединений, препятствующих этому сдвигу секции. После этого оставшиеся два соединения представляют собой два параллельных горизонтальных стержня(рис. 32.9, б). Отброшенные звенья будут заменены поперечной силой Qd-результирующим механизмом, например, возможно микродвижение угла поворота

диска BD, сообщенного BD даже при повороте BD вокруг шарнира на второй приводной угол DC так, что мгновенный центр вращения BD относительно диска DC будет бесконечным, опора 32,. Исходя из принципа возможного смещения, запишите сумму силы f=1 и боковой силы QD6£eB+ -=°>. КТ=СФ/нет. b + ^ ) — &$=Y так как мы наконец-то

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник