Построение линии пересечения кривых поверхностей способом вспомогательных секущих сфер

Построение линии пересечения кривых поверхностей способом вспомогательных секущих сфер

Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)

При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.

Существуют следующие случаи взаимного пересечения поверхностей:

1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;

2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;

3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;

4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).

Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.

Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.

Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.

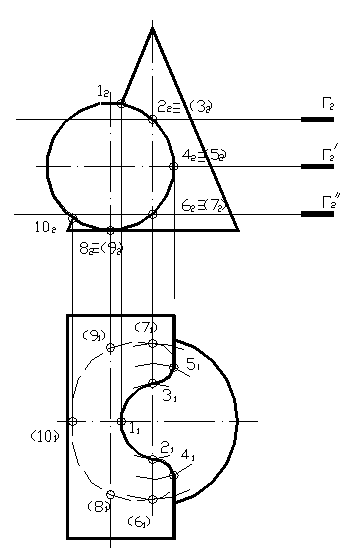
Рисунок 53

1. Какие бывают случаи взаимного пересечения поверхностей?

2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?

3. Какие точки называются опорными?

4. Как определять видимость линии пересечения и поверхностей?

5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Построение линии пересечения кривых поверхностей способом вспомогательных секущих сфер

При определении линии пересечения двух поверхностей вращения, при их особом взаимном расположении, не всегда рационально применять вспомогательные секущие плоскости. В некоторых случаях применяют метод вспомогательных секущих сфер – концентрических или эксцентрических.

Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями.

Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа, в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рис.151) или одна из осей становиться проецирующей прямой, а вторая — линией уровня (рис.152).

Рисунок 1 51. Пересечение поверхностей вращения, оси которых параллельны
фронтальной плоскости проекций.

а) модель		б) эпюр

Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.151). Эта точка принимается за центр всех вспомогательных концентрических сфер. Каждая из концентрических сфер пересекает поверхности по окружностям — параллелям (а, b, c, d, n), фронтальные проекции которых являются прямыми линиями (а₂, b₂, c₂, d₂, n₂). Проекции точек 1₂, 2₂, 3₂, 4₂, 5₂ и 6₂ пересечения проекций параллелей принадлежат проекции искомой линии пересечения поверхностей. Пересечение главных фронтальных меридианов поверхностей определяют положение верхней и нижней точек (7 и 8) линии.

Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны видимости линии пересечения поверхностей на горизонтальной проекции. Для этой цели использовалась вспомогательная секущая плоскость b , которая пересекает поверхность Q по линии m, а поверхность G по образующим, горизонтальные проекции которых пересекаясь определяют положение искомых точек.

Соединив найденные точки 1. 10 с учетом видимости получим линию пересечения поверхностей.

Рисунок 152. Пересечение поверхностей вращения,
ось одной — горизонтально проецирующая
прямая, а второй — горизонталь

Вторым примером использования в качестве вспомогательных поверхностей посредников концентрических сфер рассмотрим при определении линии пересечения поверхностей предложенных на рисунке 152. Оси поверхностей вращения G и Q пересекаются в точки А , при этом ось поверхности Q — горизонтально проецирующая прямая, а ось поверхности G — горизонталь. Точка А принимается за центр всех вспомогательных концентрических сфер.

Точки 1 и 2 линии пересечения построены с помощью сферы радиуса R. Эта сфера пересекает поверхность Q по окружности а, а поверхность G по окружности b , которая показана только на горизонтальной проекции. Пересечение горизонтальных проекций окружностей а₁ и b ₁ определяют проекции 1₁ и 2₁ точек линии пересечения. Их фронтальные проекции 1₂ и 2₂ построены на а₂ пересечении с линиями связи.

Для нахождения точек 5 и 6 определяющих границу зоны видимости на горизонтальной проекции, использовалась вспомогательная секущая плоскость b , которая пересекает поверхность Q по окружность n, а коническую поверхность G по треугольнику, определяющему ее очерк на горизонтальной проекции.

Точки 7 и 8 находятся на границе зоны видимости фронтальной проекции, для их нахождения используется вспомогательная секущая плоскость g .

Соединив найденные точки 1. 8 с учетом видимости получим линию пересечения поверхностей G и Q.

Эксцентрические сферические посредники применяются при определении точек линии пересечения поверхностей вращения с поверхностью несущей на себе непрерывное множество окружностей. Обе поверхности должны иметь общую плоскость симметрии. Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям.

Рисунок 1 53. Пересечение конуса и сферы

а) модель		б) эпюр

Определения линии пересечения конуса и сферы применение эксцентричных сфер, как поверхностей — посредников. Центры сфер — точки расположены на оси конуса. Сфера пересекает конус и сферу по окружностям , которые пересекаются в двух точках, принадлежащих искомой линии пересечения (рис.153а).

Верхняя и нижняя точки линии пересечения найдены с помощью вспомогательной секущей плоскости — плоскости главного фронтального меридиана, пересекающая конус и сферу по треугольнику и окружности, являющимися очерками поверхностей на фронтальной плоскости проекций.

Точки, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости — горизонтальной плоскости уровня, пересекающей сферу по экватору — окружности являющейся очерком шара на горизонтальной проекции, а конус по окружности — параллели.

Точки, найденные с помощью вспомогательных поверхностей посредников, определяют линию пересечения конуса и шара.

Рассмотрим, на примере определения линии пересечения конуса Q и сферы G (рис.153б), применение эксцентричных сфер, как поверхностей — посредников. Центры сфер — точки А 1 , А 2 и А 3 расположены на оси конуса. Сфера радиуса R 1 с центром в точке А 1 пересекает конус и сферу по окружностям а и в, которые пересекаются в точках 1 и 2, принадлежащих искомой линии пересечения. С помощью сферы R 2 с центром А 2 и сферы R 3 с центром А 3 определено положение точек 3, 4 и 5,6 соответственно. Точки 7 и 8 найдены с помощью вспомогательной секущей плоскости a (плоскости фронтального меридиана), пересекающей конус и сферу по главным фронтальным меридианам k и l . Точки 9 и 10, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости b (горизонтальной плоскости уровня), пересекающей сферу G по экватору s, а конус Q по окружности p. Точки 1. 10, построенные с помощью вспомогательных поверхностей посредников, определяют линию пересечения конуса и шара.

Источник

Построение линий пересечения поверхностей способом вспомогательных секущих сфер

Две любые соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения главных полумеридианов этих поверхностей. При этом плоскости окружностей сечения перпендикулярны оси поверхностей вращения, а центры окружностей принадлежат этой оси. Поэтому если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпен­дикулярных проекциям оси вращения.

В качестве вспомогательной секущей поверхности вращения целесообразно использовать удобную для вычерчивания сферическую поверхность, центр которой должен принадлежать оси поверхности вращения (рис. 1.73). Здесь сфера Σ (i,m) пересекается с поверхностью вращения Ф(i,n) по окружностям, т. к. полумеридианы поверхности вращения и сферы имеют две точки пересечения – A и В.

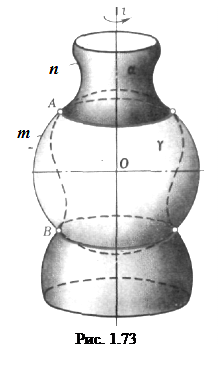
При построении линий пересечения двух поверхностей способом вспомогательных секущих сфер возможны два случая. В одном из них используют сферы, проведенные из одного общего для всех сфер центра, а в другом – сферы, проведенные из разных центров. В первом случае имеем способ концентрических сфер, во втором – способ эксцентрических сфер.

Рассмотрим каждый случай в отдельности.

1.7.4.1.Способ вспомогательных секущих концентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности вращения;

— оси поверхностей вращения пересекаются;

— плоскость, образованная пересекающимися осями (общая плоскость симметрии поверхностей), параллельна одной из плоскостей проекций. Именно на этой плоскости проекций и проводят вспомогательные секущие сферы, центр которых лежит в точке пересечения осей.

Рассмотрим пример. Построить линию пересечения цилиндра и конуса вращения, оси которых i и j пересекаются в некоторой точке Ои параллельны плоскости проекций П₂ (рис. 1.74).

Вначале должны быть построены некоторые опорные точки. Так как обе данные поверхности имеют общую плоскость симметрии, параллельную плоскости проекций П₂, то их контур­ные образующие, по отношению к плоскости П₂, пересекаются. Точки А, В, С и Dпересечения этих образующих являются точками видимости линии пересечения поверхностей. Эти точки ограничивают фронтальную проекцию линии пересечения.

Далее следует определить радиусы максимальной и минимальной сфер, пригодных для отыскания точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от проекции О₂ центра сфер до наибо­лее удаленной точки пересечения очерковых образующих, в данном случае до точки A₂.

Чтобы определить радиус наименьшей сферы R_min, необходимо провести через точку О₂нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет R_min. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а совторой – пересекаться. Если же взять в качестве R_min меньший отрезок, то одна из данных поверхностей с такой сферой не пересечется. В данном примере сферой минимального радиуса будет сфера, касающаяся цилиндрической поверхности. Эта сфера касается цилиндрической поверхности по окружности 1 – 2; коническую поверхность она пересекает по двум окружностям 3 – 4и 5 – 6. Точки Е, Fи G, Нпересечения этих ок­ружностей будут точками искомой линии пересечения.

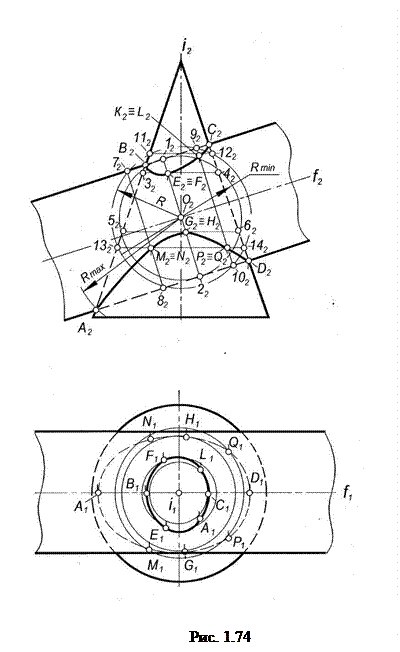
Для построения других точек линии пересечения проводят несколько концентрических сфер с центром в точке О, причем радиус Rэтих сфер должен изменяться в пределах R_min

1.7.4.2.Способ вспомогательных секущих эксцентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности, которые имеют общую плоскость симметрии;

— каждая из этих поверхностей должна содержать семейство окружностей, по которым ее могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Рассмотрим пример. Построить линию пересече­ния поверхности тора с конической поверхностью вращения, которые имеют общую фронтальную плоскость симметрии (рис. 1.75).

По аналогии с предыдущей задачей строим точки А и В пересечения контура поверхности тора с контуром конической поверхности. Точка А является наивысшей точкой искомой линии, а точка В – наинизшей.

Для построения произвольных точек линии пересечения в данной задаче нельзя воспользоваться способом вспомогательных концентрических сфер: хотя обе поверхности и являются поверхностями вращения, но их оси i 1 и i 2 не пересекаются. Способом же эксцентрических сфер, центры которых находятся в различных точках оси i 2 конической поверхности, можно найти сколько угодно произвольных точек линии пересечения.

Действительно, у поверхности тора, кроме семейства окружностей (параллелей), расположенных в плоскостях, перпендикулярных оси i 1 , имеется семейство окружностей (меридианов), расположенных в плоскостях, проходящих через ось i 1 . Центры сфер, пересекающих поверхность тора по этим окружностям, будут нахо­диться на перпендикулярах к плоскостям этих окружностей, проведенных через их центры С 1 , С 2 , С 3 , . . Поэтому если взять центры эксцентрических сфер в точках О 1 , О 2 , О 3 , . пересечения этих перпендикуляров с осью i 2 конической поверхности, то сферы соответствующих радиусов пересекут обе данные поверхности по окружностям. Точки пересечения окружностей обеих поверхностей, принадлежащих одной и той же сфере, и будут точками искомой линии пересечения.

На рис. 1.75 проведены три эксцентрические сферы из центров О 1 , О 2 и О 3 , с помощью которых найдены случайные точки линии пересечения. Так, для построения точек Ми Nпроведен меридиан 3 – 4поверхности тора, расположенный во фронтально проецирующей плоскости, проходящей через ось i 1 (i₂ 1 ), и из его центра С 1 (С_г 1 )восстановлен перпендикуляр к этой плоскости. В точке О 1 (О₂ 1 ) пересечения перпендикуляра с осью i 2 (i₂ 2 ) и будет находиться центр вспомогательной сферы. Если теперь провести сферу с центром в точке О 1 (О₂ 1 ) такого радиуса R, чтобы ей принадлежала окружность 3 – 4, то эта сфера, пересекая коническую поверхность по некоторой окружности 1 – 2, определит в пересечении окружностей 1 – 2 и 3 – 4 искомые точки Ми N.

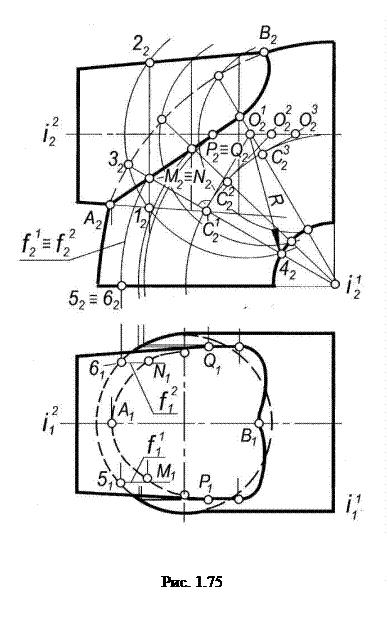
Горизонтальные проекции точек пересечения можно найти с помощью графически простых линий поверхности тора, которыми являются ее параллели. Так, горизонтальные проекции М₁ и N₁ точек Ми N построены при помощи параллелей j 1 и j 2 поверхности тора. Точки видимо­сти Ри Qконической поверхности для плоскости P₁ построены приближенно, их фронтальные проекции найдены в пересечении фронтальных проекций линии пересечения и оси i 2 конуса.

Источник

Читайте также:  Народные способы лечения кашля у взрослых