Построение линии пересечения двух криволинейных поверхностей способом вспомогательных секущих

Построение линии пересечения двух криволинейных поверхностей способом вспомогательных секущих плоскостей

Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)

При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.

Существуют следующие случаи взаимного пересечения поверхностей:

1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;

2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;

3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;

4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).

Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.

Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.

Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.

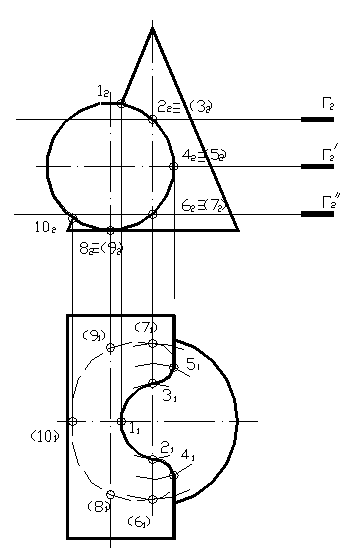
Рисунок 53

1. Какие бывают случаи взаимного пересечения поверхностей?

2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?

3. Какие точки называются опорными?

4. Как определять видимость линии пересечения и поверхностей?

5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

6.2.1 Построение линий пересечения поверхности с помощью вспомогательных секущих плоскостей

При решении задач на построение линий пересечения поверхностей вспомогательные секущие плоскости обычно выбирают в виде плоскостей уровня (плоскостей, параллельных плоскостям проекций). Линии двух поверхностей имеют характерные (опорные, главные) точки, с которых и следует начинать построение линий пересечения. Они позволяют видеть, в каких границах можно изменять положение вспомогательных секущих плоскостей для определения произвольных точек.

Способ определения линии пересечения поверхности с помощью плоскостей, — ось которого – собственная прямая.

Этот способ применяется для построения линий пересечения:

а) двух конических поверхностей;

б) конической и цилиндрической поверхности;

в) конической поверхности с поверхностью пирамиды или призмы;

г) двух цилиндрических поверхностей;

д) цилиндрической поверхности с поверхностью пирамиды или призмы.

Рассмотрим несколько следующих задач.

1. Построить линии пересечения цилиндра и конуса, оси которых

пересекаются (рисунок 6.1).

Обе данные поверхности рассечены вспомогательными плоскостями I₂, II₂, III₂ и т.д., которые параллельны плоскости П₁. На горизонтальной проекции конуса получится ряд концентрических окружностей, обозначенных теми же номерами, а на проекции цилиндра – ряд образующих.

В пересечении образующих с соответствующими окружностями определяются горизонтальные проекции точек искомого сечения а, в, с и прочие, по которым затем находят их фронтальные проекции.

Найденные проекции точек соединяют плавными кривыми. Невидимые части

линии пересечения проведены штрихами на обеих проекциях.

Границей между видимой и невидимой частями линий пересечения являются крайние образующие цилиндра.

Такие наиболее характерные точки линий пересечения кривых поверхностей следует строить в первую очередь, т.е. начинать работу с определения точек, в которых крайние (очерковые) образующие каждой поверхности, ограничивающие контур видимости на П₁, П₂, пересекают другую поверхность. После этого находят проекции нескольких промежуточных точек.

Если кривая поверхность пересекается с многогранником, то контур линии пересечения состоит из нескольких кривых частей, пересекающихся между собой на ребрах многогранника, следовательно, в этих точках криволинейный контур имеет резкие изломы. Эти характерные точки следует определять в первую очередь. На рисунке 6.2 таковыми являются точки (1₁, 1₂), (2₁, 2₂), (3₁, 3₂), (4₁, 4₂), в которых ребра призмы пронизывают поверхность конуса.

В обоих рассмотренных примерах легко выбрать вспомогательные секущие плоскости так, чтобы в пересечении их с каждой из данных поверхностей получились простые линии – окружности или прямые. Особенность этих примеров состояла в том, что одна из данных поверхностей была проецирующей (т.е. ее образующие или ребра были перпендикулярны к одной из плоскостей проекций).

В таких случаях одна из проекций искомой линии уже имеется на эпюре: она совпадает с соответствующей проекцией той из данных поверхностей, которая является проецирующей (например, с профильной цилиндра на рисунке 6.1 или с фронтальной рисунке 6.2).

Вся задача, в сущности, сводится к нахождению по одной известной заранее проекции линии пересечения других ее проекций.

Затем найдены еще две характерные точки (51, 52) и (61, 62), в которых крайняя образующая конуса пересекает грани призмы. После этого можно найти проекции нескольких промежуточных точек, в которых другие образующие конуса пересекают грани призмы (71, 72; 81, 82; 91, 92; 101, 102).

Пример. Построить линию пересечения двух поверхностей — конической поверхности Δ и сферы Т (рисунок 6.3).

Заданные поверхности имеют общую (фронтальную) плоскость симметрии, определяемую осью конуса i и осью сферы i ′ .

Построение линии пересечения начнем с определения опорных точек. Сначала отмечаем очевидные общие 1 и 7 точки поверхностей в пересечении их главных меридианов δ ∩ τ, так как поверхности имеют общую фронтальную плоскость симметрии Ф (Ф₁). Фронтальные проекции точек 1₂(7₂) = δ₂ ∩ τ

Горизонтальные проекции точек 1₁= 1₂1₁∩τ₁ , 7₁= 7₂7₁∩τ₁. Эти опорные точки являются наивысшей 1 и наинизшей 7 точками линии пересечения, а также точками видимости на плоскости П₂.

Брать вспомогательные фронтальные плоскости параллельные П для построения следующих точек неудобно, так как они будут пересекать конус по гиперболам. Графически простые линии (окружности параллелей) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г. Первую такую вспомогательную плоскость Г (Г₂) берем на уровне экватора сферы h (h₂). Эта плоскость пересекает конус по параллели n . В пересечении n и h, параллелей конуса и сферы, находятся точки видимости линии пересечения на плоскости П₁ — h₁∩n₁ = 4₁(4′₁); 4₁4₂ ∩h₂ (или n₂)= 4₂(4′₂).

Промежуточные точки 6 и 6′ линии пересечения построены с помощью плоскости Г′ (Г′₂), пересекающей поверхности по параллелям h′ и m.

Аналогично построены точки 2(2′) и 3(3′) с помощью вспомогательных плоскостей Г» (Г₂»)и Г»‘ (Г₂‘»).

Видимость заданных поверхностей и точек линии пересечения на плоскости проекций П2 определяет фронтальная плоскость Ф (Ф₁). Плоскость Ф делит поверхности конуса и сферы на две симметричные части. Те части заданных поверхностей, которые расположены перед плоскостью Ф на плоскости П₂ видимы, а значит видимы и точки 2′ 3′, 4′, 5′, 6′ им принадлежащие. Точки 2, 3, 4, 5, 6 — невидимы на П2. Так как линия пересечения — кривая, симметричная относительно плоскости Ф, то на плоскости П₂ видимая ее часть и невидимая совпадают. Изображаем на чертеже видимую часть линии пересечения сплошной основной линией. Границы видимости — точки 1 и 7. Видимость заданных поверхностей и линии пересечения на плоскости проекций П₁,

определяет плоскость Г (Г₂) и поверхность сферы: та часть сферы, которая расположена над плоскостью Г на П₁, будет видима, значит и точки 1, 2′, 2, 3, 3′ на П₁ видимы, как ей принадлежащие. Точки 5, 5′, 6, 6′, — невидимы на П₁. Границы видимости — точки 4 и 4′.

Соединяем одноименные проекции построенных точек с учетом их видимости плавными кривыми и получаем проекции искомой линии пересечения.

Источник

Построение линий пересечения поверхностей способом вспомогательных секущих плоскостей

В качестве вспомогательных секущих поверхностей чаще всего используются проецирующие плоскости. Рассмотрим два примера.

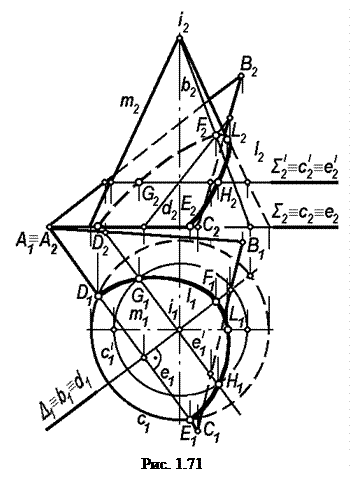
1. Построим линию пересечения конуса вращения Ф(i,m) с поверхностью, которая задана треугольником Т(АВС) (рис. 1.71).

Сначала найдем экстремальные точки, а именно самые нижние. Для этой цели проведем фронтально проецирующую вспомогательную секущую плоскость Σ, проходящую через основание конуса.

Плоскость Σ, пересекаясь с конусом Ф, даст окружность с, а с плоскостью Т – прямую е(А,В). Эти две линии пересекаются и дают две самые нижние точки D и Е линии пересечения заданных поверхностей.

Для определения самой верхней точки пересечения поверхностей целесообразно воспользоваться проецирующей секущей плоскостью Δ, след которой на горизонтальном поле проекций проведем через ось конуса i₁ в направлении,перпендикулярном горизонтальной проекции линии АС. Плоскость Δ пересекает конус по образующей b, а плоскость – по прямой d. Эти линии в свою очередь пересекаются и дают самую верхнюю точку F линии пересечения заданных поверхностей.

Воспользовавшись фронтально проецирующей секущей плоскостью Σ I , получаем две произвольные точки G и H, которые позволяют более полно представить форму линии пересечения l конуса вращения и плоскости.

Представляет интерес особая точка L линии l, т. к. она принадлежит фронтальному очерку конуса Ф, и поэтому в этой точке видимая часть линии l переходит в невидимую, что наглядно показано на фронтальном поле проекций комплексного чертежа (рис 1.71).

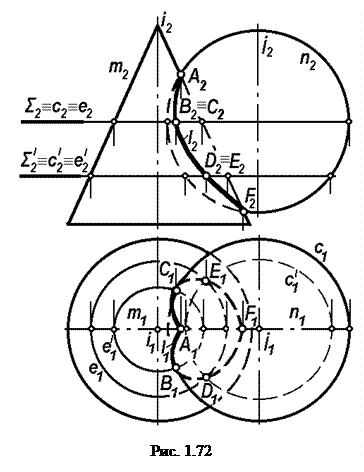
2. Построим линию пересечения двух криволинейных поверхностей: конуса вращения Ф(i,m) и сферы Т(j,n) (рис. 1.72).

Самая верхняя А и самая нижняя F точки линии пересечения l этих поверхностей в рассматриваемом примере могут быть найдены на пересечении фронтальных очерков конуса и сферы.

Если воспользоваться фронтально проецирующей вспомогательной секущей плоскостью Σ, то можно найти точки В и С линии l,которые принадлежат горизонтальному очерку сферы. Следовательно, эти точки определяют на горизонтальном поле проекций переход видимой части в невидимую часть линии пересечения l.

Воспользовавшись фронтально проецирующей секущей плоскостью Σ I , получаем две произвольные точки D и E, которые позволяют более полно представить форму линии пересечения l конуса вращения и сферы.

Источник

Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей

Федеральное государственное образовательное учреждение

«Астраханский государственный технический университет»

Кафедра начертательной геометрии

и инженерной графики

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ

Методические указания для студентов первых курсов

всех технических специальностей

Составители: к. т.н. профессор ,

Рецензент: доцент кафедры НГГ

Рассмотрено и утверждено на заседании кафедры «Начертательной геометрии и инженерной графики»

Протокол № от «___» __________20 г.

Цель работы. Применение метода вспомогательных секущих плоскостей для построения линии пересечения двух поверхностей.

1. Вычертить условие задачи.

2. Построить характерные (опорные) и промежуточные точки линии пересечения поверхностей заданным методом.

3. Построить линию пересечения поверхностей.

4. Определить видимость проекций.

1 Общий алгоритм построения линии пересечения двух кривых поверхностей

Две кривые поверхности пересекаются по пространственной кривой линии, которая графически строится по отдельным точкам. Основной метод построения линии пересечения состоит в применении вспомогательных секущих поверхностей – посредников F.

Поверхности F выбираются такими, чтобы они пересекали данные поверхности Ф’ и Ф” по наиболее простым линиям — прямым или окружностям. Точки пересечения (I, II) этих линий и будут принадлежать искомой линии пересечения поверхностей (рисунок 1).

Рисунок 1 — Иллюстрация алгоритма построения линии пересечения поверхностей

Пространственный алгоритм состоит из следующих операций:

В зависимости от вида секущих поверхностей-посредников рассматриваются два способа построения линии пересечения поверхностей.

1) Способ вспомогательных секущих плоскостей;

2) Метод вспомогательных секущих сфер.

2 Метод вспомогательных секущих плоскостей

Метод вспомогательных секущих плоскостей применяется для построения:

а) поверхности многогранника и кривой поверхности;

б) двух поверхностей вращения с параллельными или скрещивающимися осями;

в) двух конических или цилиндрических, или конической и цилиндрической поверхностей общего вида.

2.1 Построение линии пересечения поверхности многогранника

с кривой поверхностью

Линия пересечения многогранника с кривой поверхностью имеет форму кривой с точками излома на ребрах многогранника.

Пример 1. Построить линию пересечения треугольной пирамиды с цилиндром вращения. (рисунок 2).

Линии пересечения треугольной пирамиды с поверхностью цилиндра вращения являются тремя дугами эллипсов, которые пересекаются между собой в точках пересечения А (А1,А2), В (В1,В2), С (С1,С2) ребер пирамиды с поверхностью цилиндра.

Горизонтальной проекцией этих дуг эллипсов является окружность – горизонтальная проекция цилиндра вращения.

Найдем ряд точек на фронтальной проекции. Фронтальные проекции D2, Е2 точек D и Е находим на фронтальной проекции основания пирамиды путем проведения линий связи через точки D1 и Е1 (т. е. через точки основания перпендикуляров из S1 на L1P1 и P1T1).

Точки видимости М2 и N2 найдем по принадлежности их боковым граням пирамиды, проводя через М1 и N1 горизонтальные проекции горизонталей.

Фронтальные проекции К2, F2,G2 и т. д. вспомогательных точек К, F, G и т. д. так же найдем из условия их инцидентности.

Найдя достаточное количество точек, соединяем их плавными кривыми.

Рисунок 2 – Построение линии пересечения пирамиды с цилиндром

2.2 Построение линии пересечения двух кривых поверхностей,

одна из которых – проецирующая

Пример 2. Построить линию пересечения цилиндра с конусом (рисунок 3).

В этом примере цилиндр является горизонтально-проецирующей поверхностью. Следовательно, известны горизонтальные проекции всех точек искомой линии пересечения. Так как точки пересечения принадлежат конической поверхности, можно построить их фронтальные проекции.

Построение следует начинать с характерных точек. Высшая (В2) и низшая (А2) точки лежат в горизонтально-проецирующей плоскости (11-21), проходящей через оси цилиндра и конуса (горизонтальные проекции точек А и В – А1 и В1).

Границей видимости (С2, D2) линии пересечения на фронтальной плоскости проекций являются горизонтальные проекции точек С и D.

Точки Е и F расположены на образующих конуса, которые являются очерковыми на фронтальной плоскости проекций. Точки М и N также являются опорными.

Для получения их проекций, как и промежуточных точек линии пересечения, намечают ряд горизонтальных проекций точек. Для получения фронтальной проекции этих точек проводят через их горизонтальные проекции одноименные проекции образующих конуса, строят фронтальные проекции этих образующих, и на них находят фронтальные проекции искомых точек (М2, N2).

Вместо образующих можно использовать параллели конической поверхности, которые на горизонтальную плоскость проецируются в виде окружностей.

На рисунке 3 параллель К2К’2 проведена через точку L.

Горизонтальной проекцией этой параллели является окружность, проходящая через точки L1 и L’1. Фронтальные проекции этих точек лежат на прямой К2К’2.

Соединяя полученные точки плавной кривой, получим фронтальную проекцию искомой линии пересечения поверхностей.

Часть линии пересечения от точки С2 через точки А2, М2 до точки D2 видимая, остальная ее часть (В2, N2, L2, Е2, С2) – невидимая.

Рисунок 3 – Построение линии пересечения цилиндра с конусом

Пример 3. Построить линию пересечения поверхности шара с цилиндром (рисунок 4).

Так как цилиндрическая поверхность фронтально-проецирующая, фронтальная проекция линии пересечения известна. Для построения горизонтальной проекции намечается на фронтальной проекции цилиндра ряд точек.

Построение начинают с характерных точек линии пересечения: высшей (точка А2), низших (точки В1, В’1), точки перехода от видимой части линии пересечения до невидимой (С1, С1′).

Горизонтальные проекции точек А и D находятся без построения, т. к. они лежат на очерковой окружности, которая на горизонтальной плоскости проецируется в прямую, совпадающую с горизонтальной осью.

Для нахождения промежуточных точек проводят на фронтальной проекции ряд параллелей, которые на горизонтальную проекцию спроецируются в виде окружностей. Пересечение окружности с образующими цилиндра дает искомые точки.

Соединяя их плавной кривой, получим искомую линию пересечения. Часть этой линии от точки А1 через точки F1′, F1 до точек С1, С’1 – видимая, остальная часть (Е1, В1, D1, …) – невидимая.

Рисунок 4 – Построение линии пересечения шара и цилиндра

2.3 Построение линии пересечения двух кривых поверхностей

введением вспомогательных секущих плоскостей

Пример 4..Построить линию пересечения конуса вращения и сферы (рисунок 5).

Заданные поверхности имеют общую (фронтальную) плоскость симметрии, определяемую осью конуса i и осью сферы i‘.

Построение линии пересечения начинаем с определения опорных точек. Сначала отмечаем очевидные общие 1 и 7 точки поверхностей в пересечении их главных меридианов δ и τ, так как поверхности имеют общую фронтальную плоскость симметрии Ф (Ф1). Фронтальные проекции точек 12 , 72 ≡ δ2 ∩ τ2.

Горизонтальные проекции точек 11 ≡ 12 11 ∩ τ1, 71 ≡ 72 71 ∩ τ1.

Эти опорные точки являются наивысшей 1 и наинизшей 7 точками линии пересечения, а также точками видимости на плоскости П2.

Выбирать вспомогательные фронтальные плоскости уровня, параллельные П2, для построения последующих точек неудобно, так как они будут пересекать конус по гиперболам. Графически простые линии (окружности параллелей) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г2.

Первую такую вспомогательную плоскость Г (Г2) берем на уровне экватора сферы h (h2). Эта плоскость пересекает конус по параллели n. В пересечении n и h (параллелей конуса и сферы) находятся точки видимости линии пересечения на плоскости П1:

Промежуточные точки 6 и 6′ линии пересечения построены с помощью плоскости Г ‘ (Г2′), пересекающей поверхности по параллелям h и m.

Аналогично построены точки 2(2′) и 3(3′) с помощью вспомогательных плоскостей Г » (Г2») и Г »’(Г2»’).

Рисунок 5 – Построение линии пересечения конуса

Видимость заданных поверхностей и точек линии пересечения на плоскости проекций П2 определяет фронтальная плоскость Ф (Ф1). Плоскость Ф делит поверхности конуса и сферы на две симметричные части. Те части заданных поверхностей, которые расположены перед плоскостью Ф, на плоскости П2 видимы, а значит видимы и точки 2′, 3′, 4′, 5′, 6′, им принадлежащие. Точки 2, 3, 4, 5, 6 – невидимы на П2. Так как линия пересечения – кривая, симметричная относительно плоскости Ф, то на плоскости П2 видимая ее часть и невидимая совпадают. Изображаем на чертеже видимую часть линии пересечения сплошной основной линией. Границы видимости – точки 1 и 7.

Видимость заданных поверхностей и линий пересечения на плоскости проекций П1 определяет плоскость Г (Г2) и поверхность сферы: та часть сферы, которая расположена над плоскостью Г2, на П1 будет видима, значит и точки 1, 2′, 2, 3, 3′ на П1 видимы, как ей принадлежащие. Точки 5, 5′, 6, 6 ‘ – невидимы на П1. Границы видимости – точки 4 и 4′.

Соединяем одноименные проекции построенных точек с учетом их видимости плавными кривыми и получаем проекции искомой линии пересечения.

Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии (рисунок 6), то самую высокую 1 и самую низкую 2 точки линии пересечения поверхностей легко определить, построив изображения этих поверхностей на плоскости П4, параллельной осевой плоскости ∑ (∑1) данных поверхностей.

Можно строить проекции всей линии пересечения в системе плоскостей П1 ^ П4, а затем построить ее фронтальную проекцию в проекционной связи с горизонтальной проекцией, замеряя высоты точек на плоскости П4, так как это показано на рисунке 6 для точек 1 и 2.

Рисунок 6 – Пересечение поверхностей вращения, не имеющих общей плоскости

симметрии, методом замены плоскостей проекций

3 Вопросы для самопроверки

1. В чем заключается способ вспомогательных поверхностей, применяемый для построения линии пересечения двух кривых поверхностей?

2. На какие виды подразделяется способ вспомогательных поверхностей?

3. Что называется экстремальными точками? Точками видимости?

4. Какие точки называются случайными?

5. Когда применяется способ вспомогательных секущих плоскостей?

1. и др. Начертательная геометрия. — М.: Высшая школа, 1963.-420 с.

2. , , Якунин начертательной геометрии (на базе ЭВМ). – М.: Высшая школа. – 1983.

3. Иванов геометрия. – М.: Машиностроение, 1995. – 224 с.

4. Харах геометрия на базе алгоритмизации и ЭВМ. Астрахань: Изд-во Астрахан. гос. технич. ун-та, 1995 – 106с.

5 Варианты заданий для самостоятельной работы

1 Общий алгоритм построения линии пересечения двух кривых

2 Метод вспомогательных секущих плоскостей……………………..4

2.1 Построение линии пересечения поверхности

многогранника с кривой поверхностью……..……………………..4

2.2 Построение линии пересечения кривых поверхностей,

одна из которых – проецирующая…..…………………………. …6

2.3 Построение линии пересечения двух кривых поверхностей

введением вспомогательных секущих плоскостей………………..9

3 Вопросы для самопроверки…………………………………………14

Источник