Построение линии пересечения двух криволинейных поверхностей способом вспомогательных

8.4 Построение линии пресечения двух поверхностей методом секущих сфер (концентрических сфер посредников)

Этот способ применяется для построения линии пересечения двух поверхностей вращения при условии, что оси поверхностей пересекаются между собой и параллельны одной из плоскостей проекций. Известно, что если сфера имеет центр на оси заданной поверхности вращения и пересекает эту поверхность, то линия пересечения будет окружностью. Если к тому же ось вращения заданной поверхности параллельна одной из плоскостей проекций , то указанная окружность проецируется на эту плоскость в отрезок прямой, перпендикулярной проекции оси вращения на ту же плоскость. На рис. 8.18 показано построение линии пересечения параболоида вращения с конусом вращения.

Для нахождения искомой линии в начале следует провести плоскость-посредник Р через оси заданных поверхностей и найти линии ее пересечения с параболоидом и конусом. На плоскости П₂ эти линии будут очерками заданных поверхностей. Точки 1₂, 2₂, 3₂, 4₂ пересечение очерченных линий рассматриваемых поверхностей принадлежат искомой линии перехода. Для нахождения других точек линии сечения опишем из точки О сферу таким радиусом, чтобы она пересекала заданные поверхности. На плоскости П₂ эта сфера проецируется в окружность, пересекающую очерки параболоида в точках А₂, В₂, С₂, D₂ и конусов в точках Е₂, F₂, G₂, H₂. Отрезки А₂В₂ и С₂D₂ являются проекциями на П₂ окружностей, по которым проведенная сфера пересекается с параболоидом. Отрезки E₂F₂ и G₂H₂ -проекции на П₂ окружностей, по которым та же сфера пересекается с конусом. Точка 5₂=C₂D₂E₂F₂ и точка 6₂=C₂D₂G₂H₂ принадлежат проекции на П₂ искомых линий перехода (в данном случае их две). Число сфер-посредников следует брать таким, чтобы полученных точек искомой линии перехода было достаточно для ее построения.

Найденные точки 1₂, 5₂, 2₂ и 3₂, 6₂, 4₂ нужно соединить плавными кривыми, которые и будут видимыми участками фронтальных проекций искомых линий перехода. Границей видимых этих линий на П₂ является очерковая линия заданного параболоида невидимые участки проекции линии перехода совпадают с видимыми и потому невидимые точки 5′₂ и 6′₂ на рис. 8.18 не показаны.

Если требуется построить и горизонтальную проекцию, то на П₁ проводят окружность, в которую проецируются линии пересечения параболоида с каждой сферы-посредником, и на этих окружностях находят точки 5₁, 5′₁ и 6₁, 6′₁. Точки 1₁, 2₁, и 3₁, 4₁ находятся на следе Г₁. Соединение полученных горизонтальных проекций точек линий перехода должно быть произведено в следующем порядке: 1₁, 5₁, 2₁, 5′₁, 1₁, и 3₁, 6₁, 4₁, 6′₁, 3₁. Границами видимости этих кривых на полкости П₁ будут очерковые образующие конусы.

8.5 Особые случаи пересечения поверхностей второго порядка.

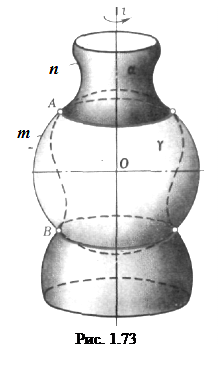
На рис. 8.19, 8.20, 8.21 изображены три случая пересечения цилиндра и конуса вращения. В первом случае рис. 8.19 цилиндр врезается в конус, потому что, если вписывать в конус сферу с центром в точке пересечения осей поверхностей, то радиус ее будет больше радиуса цилиндра. Все образующие цилиндра пересекаются с поверхностью конуса. Во втором случае рис. 8.20 конус врезается в цилиндр, т. к. сфера, вписанная в цилиндр, пересекает конус. Все образующие конуса пересекают поверхность цилиндра. В третьем случае рис. 8.21 сфера, вписанная в одну поверхность, касается второй поверхности, и в пересечении участвуют все образующие и цилиндра и конуса в этом случае пространственная линия пересечения поверхностей распадается на две плоские кривые (эллипсы).

Это положение подтверждается теоремой Монжа: Если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка, то они пересекаются по двум кривым второго порядка. Такие поверхности имеют две точки, в которых они касаются друг друга, или говорят что поверхности имеют двойное соприкосновение. Линия пересечения двух поверхностей вращения, имеющих двойное прикосновение, распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения (рис. 8.22). Две цилиндрические поверхности вращения одного диаметра касаются друг друга в точках А и В или имеют общие касательные плоскости Ф1 и Ф2. Линия АВ занимает фронтально проецирующее положение, поэтому плоскости кривых пересечения будут фронтально проецирующими. Эллипсы ACBF иAEBD изображаются отрезами прямых на фронтальной плоскости проекций и окружностями, совпадающими с выраженной проекцией вертикального цилиндра на горизонтальной плоскости проекций. Это положение широко используется при изображении пересекающихся труб или отверстий одного диаметра (рис. 8.23).

Источник

Построение линий пересечения поверхностей способом вспомогательных секущих сфер

Две любые соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения главных полумеридианов этих поверхностей. При этом плоскости окружностей сечения перпендикулярны оси поверхностей вращения, а центры окружностей принадлежат этой оси. Поэтому если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпен­дикулярных проекциям оси вращения.

В качестве вспомогательной секущей поверхности вращения целесообразно использовать удобную для вычерчивания сферическую поверхность, центр которой должен принадлежать оси поверхности вращения (рис. 1.73). Здесь сфера Σ (i,m) пересекается с поверхностью вращения Ф(i,n) по окружностям, т. к. полумеридианы поверхности вращения и сферы имеют две точки пересечения – A и В.

При построении линий пересечения двух поверхностей способом вспомогательных секущих сфер возможны два случая. В одном из них используют сферы, проведенные из одного общего для всех сфер центра, а в другом – сферы, проведенные из разных центров. В первом случае имеем способ концентрических сфер, во втором – способ эксцентрических сфер.

Рассмотрим каждый случай в отдельности.

1.7.4.1.Способ вспомогательных секущих концентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности вращения;

— оси поверхностей вращения пересекаются;

— плоскость, образованная пересекающимися осями (общая плоскость симметрии поверхностей), параллельна одной из плоскостей проекций. Именно на этой плоскости проекций и проводят вспомогательные секущие сферы, центр которых лежит в точке пересечения осей.

Рассмотрим пример. Построить линию пересечения цилиндра и конуса вращения, оси которых i и j пересекаются в некоторой точке Ои параллельны плоскости проекций П₂ (рис. 1.74).

Вначале должны быть построены некоторые опорные точки. Так как обе данные поверхности имеют общую плоскость симметрии, параллельную плоскости проекций П₂, то их контур­ные образующие, по отношению к плоскости П₂, пересекаются. Точки А, В, С и Dпересечения этих образующих являются точками видимости линии пересечения поверхностей. Эти точки ограничивают фронтальную проекцию линии пересечения.

Далее следует определить радиусы максимальной и минимальной сфер, пригодных для отыскания точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от проекции О₂ центра сфер до наибо­лее удаленной точки пересечения очерковых образующих, в данном случае до точки A₂.

Чтобы определить радиус наименьшей сферы R_min, необходимо провести через точку О₂нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет R_min. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а совторой – пересекаться. Если же взять в качестве R_min меньший отрезок, то одна из данных поверхностей с такой сферой не пересечется. В данном примере сферой минимального радиуса будет сфера, касающаяся цилиндрической поверхности. Эта сфера касается цилиндрической поверхности по окружности 1 – 2; коническую поверхность она пересекает по двум окружностям 3 – 4и 5 – 6. Точки Е, Fи G, Нпересечения этих ок­ружностей будут точками искомой линии пересечения.

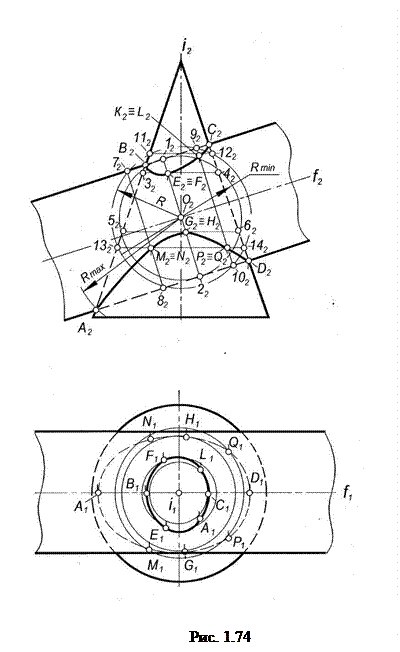
Для построения других точек линии пересечения проводят несколько концентрических сфер с центром в точке О, причем радиус Rэтих сфер должен изменяться в пределах R_min

1.7.4.2.Способ вспомогательных секущих эксцентрических сфер.

Этот способ можно использовать, если выполняются следующие условия:

— пересекаются две поверхности, которые имеют общую плоскость симметрии;

Читайте также:  Способы урегулирования конфликта с примерами

— каждая из этих поверхностей должна содержать семейство окружностей, по которым ее могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Рассмотрим пример. Построить линию пересече­ния поверхности тора с конической поверхностью вращения, которые имеют общую фронтальную плоскость симметрии (рис. 1.75).

По аналогии с предыдущей задачей строим точки А и В пересечения контура поверхности тора с контуром конической поверхности. Точка А является наивысшей точкой искомой линии, а точка В – наинизшей.

Для построения произвольных точек линии пересечения в данной задаче нельзя воспользоваться способом вспомогательных концентрических сфер: хотя обе поверхности и являются поверхностями вращения, но их оси i 1 и i 2 не пересекаются. Способом же эксцентрических сфер, центры которых находятся в различных точках оси i 2 конической поверхности, можно найти сколько угодно произвольных точек линии пересечения.

Действительно, у поверхности тора, кроме семейства окружностей (параллелей), расположенных в плоскостях, перпендикулярных оси i 1 , имеется семейство окружностей (меридианов), расположенных в плоскостях, проходящих через ось i 1 . Центры сфер, пересекающих поверхность тора по этим окружностям, будут нахо­диться на перпендикулярах к плоскостям этих окружностей, проведенных через их центры С 1 , С 2 , С 3 , . . Поэтому если взять центры эксцентрических сфер в точках О 1 , О 2 , О 3 , . пересечения этих перпендикуляров с осью i 2 конической поверхности, то сферы соответствующих радиусов пересекут обе данные поверхности по окружностям. Точки пересечения окружностей обеих поверхностей, принадлежащих одной и той же сфере, и будут точками искомой линии пересечения.

На рис. 1.75 проведены три эксцентрические сферы из центров О 1 , О 2 и О 3 , с помощью которых найдены случайные точки линии пересечения. Так, для построения точек Ми Nпроведен меридиан 3 – 4поверхности тора, расположенный во фронтально проецирующей плоскости, проходящей через ось i 1 (i₂ 1 ), и из его центра С 1 (С_г 1 )восстановлен перпендикуляр к этой плоскости. В точке О 1 (О₂ 1 ) пересечения перпендикуляра с осью i 2 (i₂ 2 ) и будет находиться центр вспомогательной сферы. Если теперь провести сферу с центром в точке О 1 (О₂ 1 ) такого радиуса R, чтобы ей принадлежала окружность 3 – 4, то эта сфера, пересекая коническую поверхность по некоторой окружности 1 – 2, определит в пересечении окружностей 1 – 2 и 3 – 4 искомые точки Ми N.

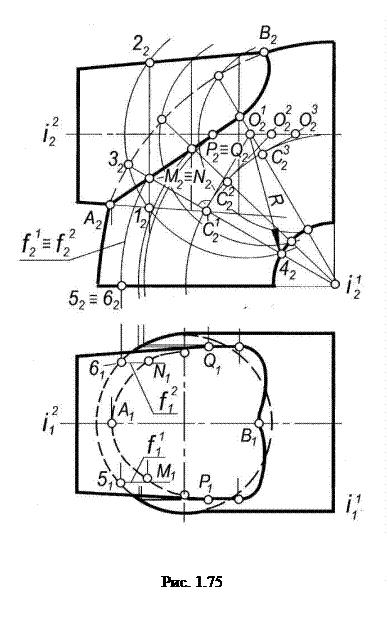
Горизонтальные проекции точек пересечения можно найти с помощью графически простых линий поверхности тора, которыми являются ее параллели. Так, горизонтальные проекции М₁ и N₁ точек Ми N построены при помощи параллелей j 1 и j 2 поверхности тора. Точки видимо­сти Ри Qконической поверхности для плоскости P₁ построены приближенно, их фронтальные проекции найдены в пересечении фронтальных проекций линии пересечения и оси i 2 конуса.

Источник