- «построение графиков функций различными способами» план-конспект урока по алгебре (10 класс) по теме
- Скачать:
- Предварительный просмотр:
- Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции. план-конспект занятия по алгебре (10, 11 класс)
- Скачать:
- Предварительный просмотр:
«построение графиков функций различными способами»
план-конспект урока по алгебре (10 класс) по теме
конспект урока по алгебре и началам анализа в 10 класс по теме «Построение графиков функций»
Скачать:
| Вложение | Размер |
|---|---|
| postroenie_grafikov_funkciy.doc | 116.5 КБ |
Предварительный просмотр:
МОУ Краснозаводская средняя школа №7
Урок-консультация в 11 классе
по алгебре и началам анализа
Павлинова Марина Вячеславовна
«Построение графиков функций элементарными методами».
Цель урока : Закрепление навыков построения графиков функций элементарными методами, формирование умения строить графики функций с помощью основных операций над графиками функций, воспитание настойчивости для достижения конечного результата, развитие навыков самоконтроля, взаимопомощи.
Оборудование : переносная магнитная доска, плакаты с готовыми графиками функций, таблица «Схема построения графика сложной функции».
- Сообщение темы и целей урока-консультации: познакомить с еще одним способом построения графиков сложной функции без применения производной; научить применять данный способ на конкретных примерах.
- Проверка домашнего задания.
-плакат с графиком функции закреплён на магнитной доске,
— плакат с графиком функции закреплён на магнитной доске,
-другие графики функций учащиеся готовят на классной доске
Учащиеся отвечают сначала по плакатам, затем по чертежам,
- Формирование новых знаний и умений учащихся.
Вы уже знаете, как строить графики функций с помощью производной, преобразований графиков функций, с помощью асимптот. Сегодня, вы узнаете ещё один способ построения графиков сложных функций на примере функций вида:
f(kx+b) и f(ax 2 +bx+c).
Рассмотрим алгоритм построения графиков таких функций (плакат на переносной магнитной доске):
а) Найти область определения функции y=f (k x+b) или y=f (a x 2 +b x+c);
b) Разбить функцию на две: z (x)= k x+b или g (x)= a x 2 +b x+c
и y=f (z) или y=f (g);
с) Построить график функции z (x)= k x+b или g (x)= a x 2 +b x+c
и отметить особые точки (точки пересечения с осями координат, промежуточные точки);
d) Произвести заданные операции над ординатами выбранных точек, то есть вычислить значения y=f (z n ) или y=f (g n );
e) Нанести полученные точки на рисунок, так чтобы ось z и ось y лежали на одной прямой, соединить отмеченные точки плавной линией.
Разберём этот алгоритм на примере функции y= (2-).
1. D(y)=R, z (x)= , y (z)=z 3 (x).
2. Построим график функции z (x)= , отметим точки пересечения с осями координат, А (0;2) и С (6;0) и ещё две промежуточные точки В (3;1) и D (12;-2).
3. Вычислим ординаты этих точек:
z 1 =2 3 =8 z 2 = 0 3 =0 z 3 =1 3 =1 z 4 =(-2) 3 =-8
4. Наносим новые точки на рисунок
А 1 (0;8) В 1 (3;1) С 1 (6;0) D 1 (12;-8).
5. Плавной линией соединяем полученные точки.
- Закрепление знаний и умений учащихся.
По одному ученику от группы идут к доске и выполняют построение графика функции своей группы. Остальные члены групп работают на местах. При затруднении ученика у доски члены группы могут проконсультировать товарища.
Задания по группам:
- Рассмотрим построение графика функции вида y=f (a x 2 +b x+c).
а) Повторить алгоритм построения графика квадратичной функции;
b) Построить график функции: y =(x 2 -4x+3) 2
1.D (y)=R, g(x)= x 2 -4x+3 y(x)=g 2 (x)
Строим параболу по точкам: А(0;3), В(1;0), С(2;-1), D(3;0), E(4;3).
Найдём ординаты этих точек.
g 1 =3 2 =9, g 2 =0 2 =0, g 3 =(-1) 2 =1, g 4 =0 2 =0, g 5 =3 2 =9.
Наносим новые точки на рисунок, плавной линией соединяем полученные точки.
- Групповая работа. На миллиметровой бумаге построить графики функций:
- Домашнее задание: доделать задание, начатое на уроке.
- Итоги урока:
Какими способами можно построить графики функций?
По какому алгоритму можно построить графики функций вида y=f (k x+b) и y=f (a x 2 +b x+c).
Решение задач домашней работы.
Построить график функции
Построить график функции
2 Прямые х=2 и х=-4 — вертикальные асимптоты
3 Промежутки знакопостоянства
4 , значит у =0 -горизонтальная асимптота.
С учетом этого построим график функции асимптотическим методом
Источник
Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
план-конспект занятия по алгебре (10, 11 класс)
Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
Скачать:
| Вложение | Размер |
|---|---|
| 80_funktsii_oblast_opredeleniya_i_mnozhestvo_znacheniy.doc | 136 КБ |
Предварительный просмотр:
Тема: Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
- дать определение понятий «функция», «область определения», «область значений», «график функции»;
- рассмотреть способы задания функций;
- рассмотреть свойства функций (нули функций, промежутки знакопостоянства, промежутки возрастания и убывания функции, четность и нечетность функции)
- рассмотреть свойства некоторых элементарных функций
Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x ). (Читают: у равно f от х .) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х .
Все значения независимой переменной образуют область определения функции . Все значения, которые принимает зависимая переменная, образуют область значений функции .
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы;
2. табличный способ (функция задается с помощью таблицы)
3. описательный способ (функция задается словесным описанием)
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Нуль функции – такое значение аргумента, при котором значение функции равно нулю .
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3. Возрастание (убывание) функции.
Возрастающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция у = f (x) называется возрастающей на интервале (а; b), если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 ) 2 ).
Убывающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Функция у = f (x) называется убывающей на интервале (а; b) , если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 )>f(x 2 ).
4. Четность (нечетность) функции
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Например, у = х 2 — четная функция.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Например: у = х 3 — нечетная функция .
Функция общего вида не является четной или нечетной ( у = х 2 +х ).
Свойства некоторых функций и их графики
1. Линейной функцией называется функция вида , где k и b – числа.
Область определения линейной функции – множество R действительных чисел.
Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b ) и параллельная прямой у = kx.
Прямая, не параллельная оси Оу, является графиком линейной функции.
Свойства линейной функции.
1. При k > 0 функция у = kx + b возрастающая в области определения.
2. При k 0 функция у = kx + b убывающая в области определения.
3. Множеством значений функции y = kx + b(k ≠ 0 ) является вся числовая прямая, т.е. множество R действительных чисел.
При k = 0 множество значений функции у = kx + b состоит из одного числа b.
3. При b = 0 и k = 0 функция не является ни четной, ни нечетной.
При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной.
При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.
Графиком линейной функции у = b является прямая, проходящая через точку (0; b ) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох .
5. При k > 0 имеем, что у > 0, если и у 0, если . При k 0 имеем, что у > 0, если и у
2. Функция y = x 2
Область определения этой функции — множество R действительных чисел.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x 2 , изображаем график функции.
График функции y = x 2 называется параболой.
Свойства функции у = х 2 .
1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х ≠ 0 , то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = х 2 является промежуток [0; + ∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х 2 — четная).
5. На промежутке [0; + ∞) функция у = х 2 возрастает.
6. На промежутке (-∞; 0] функция у = х 2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
Область определения этой функции — промежуток [0;+∞), т. е. все неотрицательные числа.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле , изображаем график функции.
1. Если х = 0, то у = 0, т.е. график функции имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х > 0, то у > 0, т.е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции является промежуток [0;+∞) .
4. Функция не является ни четной, ни нечетной.
5. Функция возрастающая в области определения.
6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
4. Функция y = x 3
Область определения этой функции — множество R действительных чисел,
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х 3 , изображаем график функции.
График функции у= х 3 называется кубической параболой.
Свойства функции y = x 3 .
1. Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) — начале координат.
2. Если х > 0, то у > 0, а если х 0, то у
3. Множеством значений функции у = х 3 является вся числовая прямая.
4. Если значения аргумента отличаются только знаком, то и значения функции отличаются только знаком, т.е. кубическая парабола симметрична относительно начала координат (функция у = х 3 — нечетная).
4. Функция у = х 3 возрастающая в области определения.
Область определения этой функции — множество R действительных чисел.
Пользуясь определением модуля числа х при х > О получим у = х, а при х у = — х . Таким образом, имеем:
График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х
1. Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) — начале координат.
2. Если х ≠ 0, то у > 0, т.е. все точки графика функции y = |x|, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции y = |x| является промежуток [0;+∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| — четная).
5. На промежутке [0;+∞) функция y = |x| возрастает.
6. На промежутке (-∞;0] функция y = |x| убывает.
7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.
Область определения функции: .
Область значений функции: .
2. Промежутки знакопостоянства,
Если k > 0, то у > 0 при х > 0; у х
Если k у х > 0; у > 0 при х
3. Промежутки возрастания и убывания.
Если k > 0, то функция убывает при .
4. Четность (нечетность) функции.
- Найдите область определения функции
- При каких значениях
функция принимает положительные значения?
Постройте график функции
- Постройте график функции
и укажите координаты точек пересечения этих графиков.
- Постройте график функции
Проходит ли график через точку А(-35, -65)?
- Вычислите координаты точек пересечения параболы
и прямой
- Какая из прямых у = 3х — 1, у = 2х + 4 или у = -2х проходит через начало координат? Постройте график этой функции.
Источник



 функция принимает положительные значения?
функция принимает положительные значения?
 и укажите координаты точек пересечения этих графиков.
и укажите координаты точек пересечения этих графиков.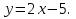
 и прямой
и прямой 



