Порядок реакции графическим способом

VIII Международная студенческая научная конференция Студенческий научный форум — 2016

ГРАФИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПОРЯДКА ХИМИЧЕСКОЙ РЕАКЦИИ

Главное в кинетике — получение кинетического уравнения любой реакции. Кинетическое уравнение связывает между собой константу скорости реакции К, текущую (С) и начальную (С0) концентрацию, время и служит для решения прямой задачи.

Известно, что процесс гидролиза сахарозы является элементарной бимолекулярной реакцией:

C12H22O11(сахароза) + H2O—> C6H12O6(глюкоза) + C6H12O6(фруктоза)

Однако в нашем случае реакция проводится в условиях большого избытка воды, поэтому концентрация воды в ходе реакции практически не изменяется и может быть включена в константу скорости; мы имеем дело с реакцией, так называемого псевдопервого порядка.

Скорость реакции гидролиза сахарозы прямо пропорциональна концентрации сахарозы в растворе. Поскольку в нейтральной среде скорость реакции очень мала, она проводится в присутствии кислоты; ионы водорода выступают в роли катализатора. Концентрация ионов водорода, не изменяющаяся в ходе реакции, также может быть включена в константу скорости реакции. В задачу данной работы, помимо определения константы скорости реакции гидролиза сахарозы, входит также и изучение её зависимости от концентрации катализатора.

Для контроля за протеканием реакции в данной работе используется один из оптических методов исследования — поляриметрический. Применение его для изучения кинетики процесса гидролиза сахарозы возможно благодаря тому, что и сахароза, и продукты гидролиза — глюкоза и фруктоза — являются оптически активными веществами, и их водные растворы вращают плоскость поляризации света. Угол вращения плоскости поляризации «α» прямо пропорционален концентрации оптически активного вещества C (в г/мл) и толщине слоя d (в см):

Коэффициент пропорциональности « » есть удельное вращение (или постоянная поляризации), которое зависит от природы вещества, длины волны поляризованного света, температуры и природы растворителя. Удельное вращение численно равно углу поворота плоскости поляризации света, прошедшего через слой толщиной 10 см раствора, содержащего 1 г вещества в 1 мл раствора и длине волны света, равной 589.6 нм (D-линия натрия).

В ходе реакции гидролиза сахарозы угол вращения плоскости поляризации изменяется, поскольку сахароза является правовращающим веществом (А = 66.55°), а эквимолярная смесь глюкозы (А = 52.50°) и фруктозы (А = — 91.90°) вращает плоскость поляризации света влево. Угол вращения плоскости поляризации света в начале реакции положительный, по мере её протекания уменьшается, стремясь к некоторому отрицательному конечному значению (т.е. происходит оптическая инверсия). Окончанию реакции соответствует некоторое предельное отрицательное значение угла вращения .

В уравнения значений концентраций сахарозы можно подставить разности соответствующих углов вращения плоскости поляризации света реакционной смесью. Тогда формулы и приобретают следующий вид:

В две пронумерованные конические колбы переносят отобранные пипеткой пробы приготовленного раствора сахарозы объёмом 25 мл. К первой пробе добавляют 25 мл раствора кислоты, полученную смесь перемешивают, помещают в поляриметрическую трубку и производят измерение угла вращения плоскости поляризации приготовленным раствором. Полученное значение принимают за начальный угол вращения αо; от момента первого измерения начинают отсчёт времени реакции. После этого аналогичные операции производят со второй пробой (во втором опыте используют раствор кислоты другой концентрации).

Измерение угла вращения плоскости поляризации производят через каждые 10 минут до тех пор, пока угол вращения не станет отрицательным (не менее 10 определений).

Оставшуюся в одной из колб после заполнения поляриметрической трубки смесь растворов сахарозы и кислоты используют для определения конечного угла вращения . Для этого смесь помещают на час в термостат с температурой 60 °С . Затем смесь охлаждают до комнатной температуры и производят измерение конечного угла вращения плоскости поляризации . Данные измерений представлены в таблице 1.

Источник

Методы определения порядка реакции

Для установления порядка реакции необходимо получить экспериментальные данные, описывающие изменение концентрации реагирующих веществ с течением времени, т.е. снять кинетическую кривую 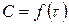. Как правило, за скоростью реакции следят по веществу, концентрацию которого легко определить химическим или физико-химическим методом.

1. Метод подстановки состоит в эмпирическом подборе кинетического уравнения такого порядка, которое наилучшим образом описывает результаты эксперимента. Существует два варианта реализации метода подстановки.

1.1. Аналитический способ заключается в расчете по опытным значениям концентраций в различные моменты времени константы скорости по уравнениям для реакций различных порядков. Уравнение удовлетворительно описывает процесс, если рассчитанные по нему значения констант колеблются около какой-либо средней величины и отклонения от среднего лежат в пределах погрешности определения.

1.2. Графический способ основан на том, что зависимость концентрации от времени для реакций различных порядков в соответствующей системе координат может быть выражена прямой линией.

Так, для реакций 0-го порядка зависимость концентрации реагирующего вещества от времени имеет линейный вид (215) (рис. 34а):

.

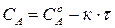
Для реакций 1-го порядка из уравнения (216) получаем прямую в системе координат 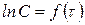(рис. 34б):

.

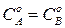
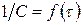
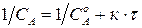
Для реакции 2-го порядка при из (219) – в координатах (рис. 34в):

.

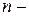
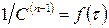
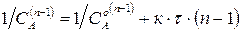
Для реакции го порядка при одинаковых исходных концентрациях реагирующих веществ из (221) – в координатах (рис. 34г):

.

Выбирают случай, когда зависимость прямолинейная. По тангенсу угла наклона определяют значение константы скорости.

Метод подстановок точен и часто применяется на практике (не только для определения порядка реакции). Недостатком метода является его трудоемкость.

2. Метод Вант-Гоффа основан на определении абсолютной скорости реакции в начальный момент времени при двух различных исходных концентрациях реагирующего вещества (рис. 35). Тогда:

; ,

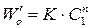
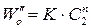
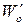
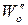
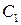
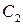
где , – скорость реакции при исходной концентрации реагирующего вещества и , соответственно;

Логарифмируя уравнения, почленно вычитая их друг из друга и решая относительно 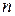, получим:

.

Метод Вант-Гоффа прост, точен и достаточно часто применяется на практике. Он позволяет находить не только целые, но и дробные порядки реакции.

3. Графический метод. Запишем кинетическое уравнение в виде:

,

.

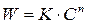
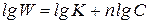
Полученное уравнение является линейным, поэтому порядок реакции 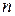будет равен тангенсу угла наклона прямой.

Недостаток метода заключается в необходимости графического определения абсолютной скорости реакции в различые моменты времени, что может привести к ошибкам.

4. Метод изоляции или избытка концентраций (Оствальда) основан на исследовании зависимости скорости реакции от начальной концентрации какого-либо одного реагента. Для этого в опытах меняют начальную концентрацию одного реагента, а другие исходные вещества берут в большом избытке – тогда концентрации этих веществ можно принять постоянными. Порядок по первому реагенту определяют одним из вышеуказанных методов. Затем проводят аналогичные опыты с переменной начальной концентрацией другого исходного вещества в избытке остальных. Общий порядок реакции равен сумме порядков по отдельным компонентам.

Кроме того, известны методы определения порядка реакции по времени полупревращения вещества, метод Оствальда-Нойеса и др.

Источник

Порядок реакции графическим способом

Общий метод определения порядка реакции основан на законе действующих масс:

. (3.1)

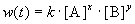
Представим, что вещество B находится в большом избытке, и его концентрация мало меняется в ходе реакции. Тогда порядок реакции по веществу A можно определить, измерив скорость реакции при двух концентрациях A. Записывая уравнение (3.1) для двух моментов времени в логарифмической форме и вычитая одно выражение из другого, найдем порядок x:

.

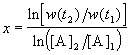
В случае, если имеется больше двух экспериментальных точек, можно записать кинетические данные в координатах lnw — ln[A] и представить их в линейном виде с помощью метода наименьших квадратов. Тогда порядок реакции x будет равен тангенсу угла наклона прямой.

Если реакция имеет целый порядок, то для определения порядка используют различные частные методы. Метод подстановки заключается в том, что кинетические данные представляют в виде

где функция f соответствует решению кинетического уравнения для одного из целых порядков. Если величина k, определенная таким образом, будет постоянной, то мы угадали, т.е. выбрали верный порядок. Если k будет изменяться со временем, то надо выбрать функцию f, соответствующую другому порядку.

Другой способ определения целого порядка заключается в измерении зависимости времени протекания реакции от начальной концентрации. Из решения (2.1) кинетического уравнения для реакции n-го порядка следует, что время t _x, за которое степень превращения достигнет x, обратно пропорционально (n-1)-й степени начальной концентрации (см. также (2.2)):

Измеряя время превращения t _x при двух начальных концентрациях, можно определить порядок n по формуле:

.

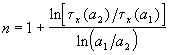
Отметим, что разные начальные концентрации можно выбирать на одной и той же кинетической кривой.

Пример 3-1. В некоторой реакции целого порядка nA B концентрация исходного вещества 0.5 моль/л была достигнута за 4 мин при начальной концентрации 1 моль/л и за 5 мин при начальной концентрации 2 моль/л. Установите порядок реакции.

Решение. Из первого опыта следует, что период полураспада вещества при начальной концентрации 1 моль/л равен 4 мин. Во втором опыте при начальной концентрации 2 моль/л период полураспада равен 1 мин (от 2 моль/л до 0.5 моль/л — за 5 мин, из них от 1 моль/л до 0.5 моль/л — 4 мин, следовательно на превращение от 2 моль/л до 1 моль/л потребовалась 1 мин).

Таким образом, при увеличении начальной концентрации в 2 раза период полураспада уменьшился в 4 = 2 n-1 раза, следовательно порядок реакции n = 3.

Пример 3-2. Кинетика реакции первого порядка, в которой происходило образование кислоты, изучалась путем отбора проб реакционной смеси и их титрования одним и тем же раствором щелочи. Объемы щелочи, которые пошли на титрование:

Время, мин

Объем, мл

Докажите, что реакция имеет первый порядок. Рассчитайте период полураспада.

Решение. Запишем решение кинетического уравнения для реакции первого порядка в виде:

,

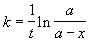
где a = x = 29.7 мл.

Время, мин

В течение реакции величина k остается постоянной, что и доказывает первый порядок.

Период полураспада равен

мин.

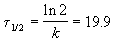
Пример 3-3. Реакция омыления метилацетата при 298 К описывается уравнением:

Для этой реакции получены следующие кинетические данные:

Время, мин

с_NaOH, ммоль/л

Исходные концентрации щелочи и эфира одинаковы и равны 0.01 моль/л. Определите порядок реакции и константу скорости.

Решение. Запишем кинетические данные в координатах lnw-lnс_NaOH, причем скорость реакции определим через конечные изменения концентраций и времени:

.

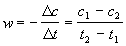
(Концентрацию вещества иногда обозначают не квадратными скобками, а буквой c). По этой приближенной формуле скорость лучше определять в середине временного интервала: t = (t₁ + t₂)/2. Концентрацию в этот момент времени определим как полусумму значений на границах интервала: c = (c₁ + c₂)/2. Сведем полученные данные в таблицу (учтем, что c_NaOH = 10 ммоль/л при t = 0):

Источник