Поразрядный способ нахождения результата деления

Конспект урока по математике на тему «Способ поразрядного нахождения результата деления» (4 класс)

Способ поразрядного нахождения
результата деления

Цели: рассмотреть способ поразрядного нахождения результата деления; учить объяснять способ поразрядного нахождения результата деления; формировать умение определять цифру разряда десятков частного в данных частных; решать задачи .

1. Можно ли, не выполняя вычислений, сказать, в какой паре записей делимые одинаковы:

: 7 = 5804 (ост. 3) : 8 = 607 (ост. 1)

: 5804 = 7 (ост. 3) : 8 = 607 (ост. 2)

2. Вставьте числа в «окошки» так, чтобы получились верные записи:

86 : = 9 (ост. 5) : 6 = 4 (ост. )

59 : = 8 (ост. 3) : 7 = 5 (ост. )

28 : = 3 (ост. 1) : 3 = 9 (ост. )

3. Из 20 счетных палочек выложите фигуру, как на рисунке:

а) Переложите семь палочек так, чтобы получить два больших и два маленьких квадрата.

б) Уберите четыре палочки так, чтобы получить один большой и пять маленьких квадратов.

II. Работа по учебнику.

Задание 234. Прочитайте задачу. Сколько мама купила яиц? Сколько она отнесла бабушке? Сколько яиц осталось? Как разделила мама оставшиеся яйца? Какие действия выполняла мама?

1) 5 : 2 = 2 (коробки; ост. 1 – яйцо без коробки);

3) 2 дес. + 5 = 25 (шт.).

– Как объединить эти действия в одну запись столбиком?

– Обведите ту часть, которая соответствует первому действию. Как получается запись окончательного результата? (К цифре 2, обозначающей первый промежуточный результат деления, приписывается цифра 5, обозначающая второй промежуточный результат деления.)

Задание 235. Учащиеся выполняют запись.

– Почему такой способ деления называют способом поразрядного нахождения результата деления?

Задание 236. Используя способ поразрядного нахождения результата деления, определите цифру разряда десятков частного в каждом случае.

7 0 : 2 – 3 дес. в частном; 80 : 4 – 2 дес. в частном;

9 0 : 3 – 3 дес. в частном; 100 : 2 – 5 дес. в частном.

70 : 5 = 1 дес. в частном.

Задание 237. Используя записанные случаи деления, найдите значения частного столбиком.

Задание 238. Для каждой записи деления столбиком запишите отдельно в строчку случаи деления, которые позволяют найти соответствующие цифры в каждом разряде частного.

Задание 239. Прочитайте задачу. Что известно? Что требуется узнать? Выполните запись деления в столбик.

Ответ: 19 букетов.

– Почему деление в столбик называют способом поразрядного нахождения результата деления?

Источник

Умники и умницы

Умные дети — счастливые родители

ПНШ 4 класс. Математика. Учебник № 1, с. 71

Способ поразрядного нахождения результата деления

Ответы к с. 71

232. Используя решение предыдущей задачи, выполни деление числа 86 на число 3 по действиям. Не забудь сложить остаток от деления десятков с числом единиц делимого.

1) 8 дес. : 3 = 2 дес. (ост. 2 дес.)
2) 2 дес. + 6 = 26
3) 26 : 3 = 8 (ост. 2)
4) 2 дес. + 8 (ост. 2) = 28 (ост. 2 шт.)

233. Сравни решение задач 230 и 232. С каким разрядом делимого выполнялось первое действие: с разрядом десятков или с разрядом единиц? В какой из задач в первом действии получился остаток? В решении какой задачи получилось больше действий? Почему?
Способ деления, при котором делимое раскладывают на разрядные слагаемые, — это СПОСОБ ПОРАЗРЯДНОГО НАХОЖДЕНИЯ результата.

С каким разрядом делимого выполнялось первое действие: с разрядом десятков или с разрядом единиц — с разрядом десятков. В каком случае в первом действии получился остаток — во втором случае. В каком случае получилось больше действий и почему — во втором случае, так как в разряде десятков при делении получили остаток, который необходимо было сложить с числом единиц делимого.
В обоих случаях использовали способ поразрядного нахождения результата деления.

234. Используя способ поразрядного нахождения результата деления, определи в частном цифру в разряде десятков.
70 : 2 92 : 3 70 : 5 82 : 4 101 : 2

Для того, чтобы получить цифру в разряде десятков значения частного нужно выполнить первый шаг алгоритма поразрядного способа нахождения результата деления: разделить число десятков делимого на делитель.
7 дес. : 2 = 3 (ост. 1 дес.) — в разряде десятков значения частного 70 : 2 будет стоять цифра 3;
9 дес. : 3 = 3 (ост. 0 дес.) — в разряде десятков значения частного 90 : 3 будет стоять цифра 3;
7 дес. : 5 = 1 (ост. 2 дес.) — в разряде десятков значения частного 70 : 5 будет стоять цифра 1;
8 дес. : 4 = 2 (ост. 0 дес.) — в разряде десятков значения частного 80 : 4 будет стоять цифра 2;
10 дес. : 2 = 5 (ост. 0 дес.) — в разряде десятков значения частного 100 : 2 будет стоять цифра 5.

235. Используя записанные ниже случаи деления, найди значение частного 96 : 4.
9 : 4 = 2 (ост. 1) и 16 : 4 = 4
Вычисли значение частного 96 : 4 по действиям.

1) 9 дес. : 4 = 2 дес. (ост. 1 дес.)
2) 1 дес. + 6 = 16
3) 16 : 4 = 4
4) 2 дес. + 4 = 24, значит 96 : 4 = 24.

Источник

Умники и умницы

Умные дети — счастливые родители

ПНШ 4 класс. Математика. Учебник № 1, с. 72

Способ поразрядного нахождения результата деления

Ответы к с. 72

236. Для данных пар чисел выполни деление с остатком способом поразрядного нахождения результата деления. Запиши решение по действиям.
84 и 7 46 и 5 62 и 2 75 и 3 100 и 7
Теперь перепиши эти же случаи деления, используя запись столбиком.
Обведи те записи, где при делении числа десятков делимого получислся остаток.

84 : 7
1) 8 дес. : 7 = 1 дес. (ост. 1 дес.)
2) 1 дес. + 4 = 14
3) 14 : 7 = 2
4) 1 дес. + 2 = 12, значит 84 : 7 = 12.

46 : 5
1) 4 дес. : 5 = 0 дес. (ост. 4 дес.)
2) 4 дес. + 6 = 46
3) 46 : 5 = 9 (ост. 1), значит 46 : 5 = 9 (ост. 1).

62 : 2
1) 6 дес. : 2 = 3 дес.
2) 2 : 2 = 1
3) 3 дес. + 1 = 31, значит 62 : 2 = 31.

75 : 3
1) 7 дес. : 3 = 2 дес. (ост. 1 дес.)
2) 1 дес. + 5 = 15
3) 15 : 3 = 5
4) 2 дес. + 5 = 25, значит 75 : 3 = 25.

100 : 7
1) 10 дес. : 7 = 1 дес. (ост. 3 дес.)
2) 3 дес. : 7 = 30 : 7 = 4 (ост. 2)
3) 1 дес. + 4 (ост. 2) = 14 (ост. 2), значит 100 : 7 = 14 (ост. 2).

_— 84 | 7 _— 46 | 5 _— 62 | 2
7 |12 45 |9 6 |31
_ 14 1 — ост. _0 2
14 2
0 0

_— 75 | 3 _— 100| 7
6 |25 7 |14
_ 15 _ 30
15 28
0 2 — ост.

Остаток в десятках получился при делении 84 : 7, 75 : 3, 100 : 7.

237. Для каждой записи деления столбиком выполни запись деления в строчку по действиям.

_— 75 | 5 _— 72 | 4 _— 81 |3
5 |15 4 |18 6 |27
_ 25 _ 32 _ 21
25 32 21
0 0 0

75 : 5
1) 7 дес. : 5 = 1 дес. (ост. 2 дес.)
2) 2 дес. + 5 = 25
3) 25 : 5 = 5
4) 1 дес. + 5 = 15 (ост. 0)

72 : 4
1) 7 дес. : 4 = 1 дес. (ост. 3 дес.)
2) 3 дес. + 2 = 32
3) 32 : 4 = 8
4) 1 дес. + 8 = 18 (ост. 0)

81 : 3
1) 8дес. : 3 = 2 дес. (ост. 2 дес.)
2) 2 дес. + 1 = 21
3) 21 : 3 = 7
4) 2 дес. + 7 = 27 (ост. 0)

238. Выполни деление с остатком чисел 77, 66, 55, 44 на число 6 по действиям. Затем для каждого случая деления выполни запись столбиком. Подчеркни случай деления нацело. Какой остаток получается в этом случае?

77 : 6
1) 7 дес. : 6 = 1 дес. (ост. 1 дес.)
2) 1 дес. + 7 = 17
3) 17 : 6 = 2 (ост. 5), значит 77 : 6 = 12 (ост. 5).

66 : 6
1) 6 дес. : 6 = 1 дес.
2) 6 : 6 = 1
3) 1 дес. + 1 = 11, значит 66 : 6 = 11.

55 : 6
1) 5 дес. : 6 = 0 дес. (ост. 5 дес.)
2) 5 дес. + 5 = 55
3) 55 : 6 = 9 (ост. 1) , значит 55 : 6 = 9 (ост. 1).

44 : 6
1) 4 дес. : 6 = 0 дес. (ост. 4 дес.)
2) 4 дес. + 4 = 44
3) 44 : 6 = 7 (ост. 2), значит 44 : 6 = 7 (ост. 2)

_— 77 | 6 _— 66 | 6
6 |12 6 |11
_ 17 _06
12 6
5 — ост. 0

_— 55 | 6 _— 44| 6
54 |9 42 |7
1 — ост. 2 — ост.

Случай деления нацело: 66 : 6, остаткок равен 0.

239. По данной записи деления с остатком столбиком назови делимое, делитель, неполное частное и остаток.

_— 87 | 21
84 |4
3

Делимое — 87, делитель — 21, неполное частное — 4, остаток — 3.

Источник

«Способ поразрядного нахождения результата деления»

Просмотр содержимого документа
««Способ поразрядного нахождения результата деления»»

-Внимание! Проверь, дружок,

Готов ли ты начать урок!

Всё ли на месте? Всё ли в порядке:

Книжки, ручки и тетрадки?

Есть у нас девиз такой:

Всё, что надо под рукой!

Итак, ребята все настроились на начало урока? Отлично. А сейчас откройте тетради и подпишите число, классная работа.

(Дети подписывают число, классная работа).

Личностные: формирование положительного отношения к учебному труду.

Коммуникативные: умение слушать друг друга, вступать в учебный диалог.

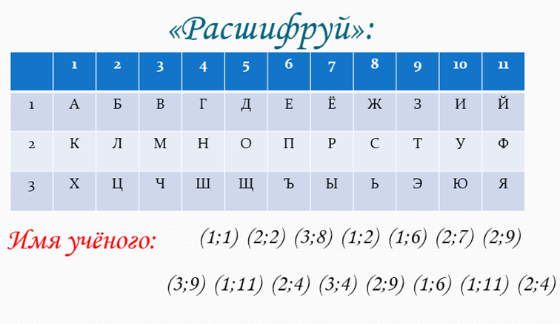
3) Расшифруй»: имя учёного физика, лауреата Нобелевской премии

6)

Ответ: 75 (Земляника)

Ответ: Альберт Эйнштейн

Ответ: 15000 + 75000 = 90000 (м 2)

Ответ: 5 * 3 = 15 ( м)

совершенствовать вычислительные навыки;

Высказывание своих мыслей с достаточной полнотой.

Строить объяснение в устной форме.

Выражение своих мыслей с достаточной полнотой и точностью.

Аргументация своего мнения и позиции.

Актуализация и фиксирование индивидуального затруднения в пробном действии.

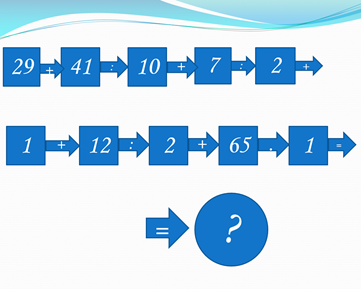
Ребята, посмотрите на доску. Давайте попробуем решить эти примеры и найти лишний

-Известен ли нам способ решения данного примера?

-Такой способ называет поразрядным способом нахождения результата деления. А почему он так называется мы узнаем в процессе урока.

-Так какую же цель мы поставим на сегодняшнем уроке?

-Ребята, а для того, чтобы узнать почему этот способ так называется, мы должны создать алгоритм решения данного примера.

Откройте учебник на странице 70. Найдите задание 229 и прочитайте его (один ученик читает).

-Давайте рассмотрим и попытаемся объяснить и прокомментировать каждое действие, записанное в решении этой задачи, а помогут нам в этом карточки на доске, которые мы должны расположить в правильном порядке

-Что сделали в 1 действии? А во втором? Что делали в последнем 3 действии?

(Работают с карточками у доски)

-У нас получился алгоритм решения примеров способом поразрядного нахождения результата. И я предлагаю вам решить один пример у доски, используя данный способ. Остальные три примера решите самостоятельно в тетради.

-Поменяйтесь тетрадями с соседом, осуществите проверку.

Дети приходят к выводу что лишним примером является 46:2 т.к. они не знают ,каким способом его решать.

«Научиться выполнять задания способом поразрядного нахождения результата деления.»

Один ученик читает).

Работа с карточками у доски:

1)4 дес. : 2 = 2 дес.- число десятков разделили на число 2 нацело;

2)6 : 2 =3 (шт.)- число единиц разделили на число 2 нацело;

3)2 дес. + 3 = 23 (шт)- выполнили сложение результатов деления в разряде десятков и в разряде единиц.

Работа с доской (карточками)

волевая саморегуляция в ситуации затруднения.

использовать речь для планирования и регуляции своей деятельности.

планировать учебные действия.

Построение проекта выхода из затруднения.

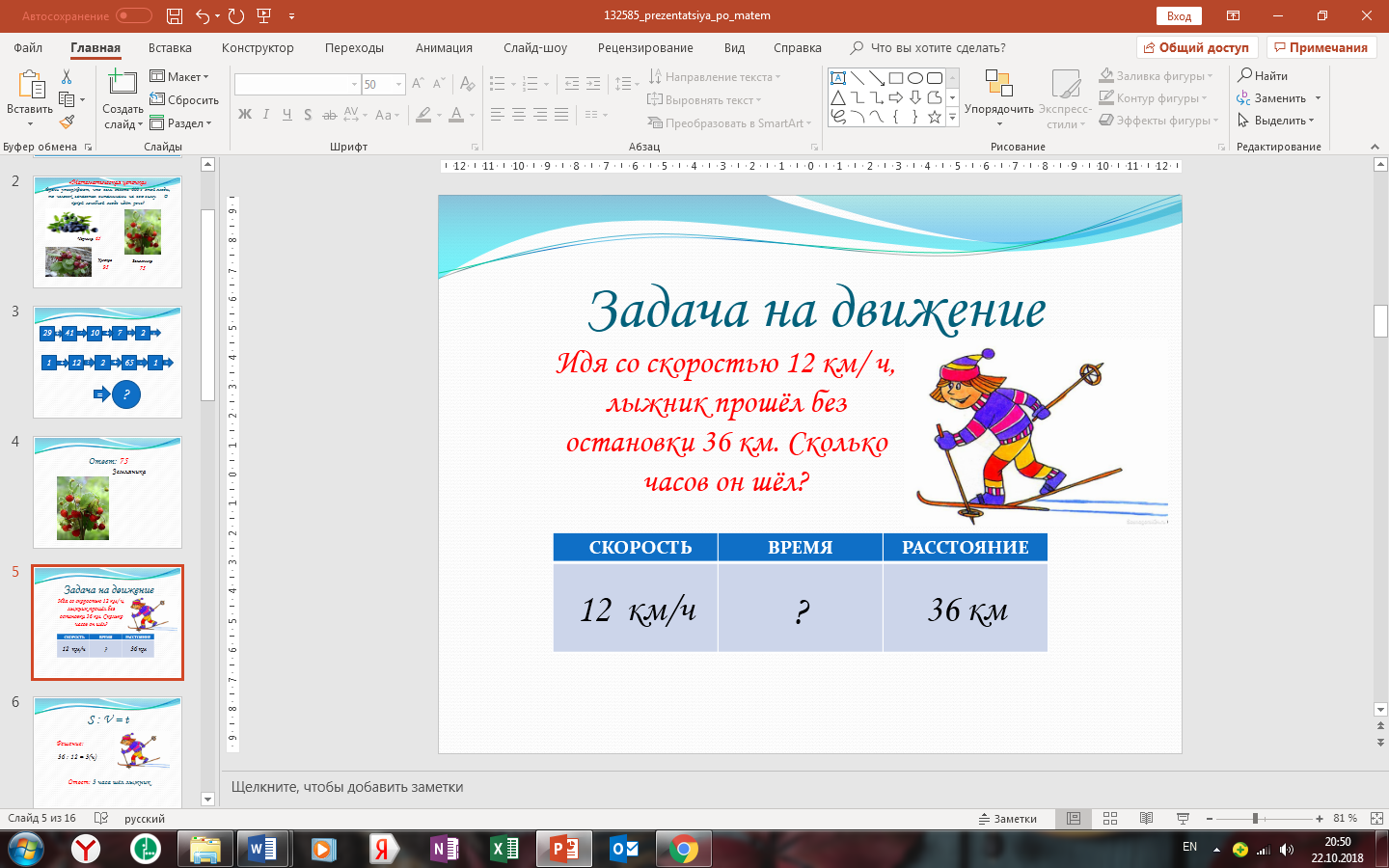
—Найдите в учебнике задание № 230.(стр 70) Давайте прочитаем задание

Используя решение предыдущей задачи выполни деление числа 96 на число 3 по действиям. Для этого разложи делимое на разрядные слагаемые. Затем раздели число десятков делимого на 3 нацело. Потом раздели количество единиц делимого на число 3. Полученные значения частных сложи.

-Попробуем решить эту задачу у доски, используя решение предыдущей задачи. Итак, с чего мы начнем?

-Во втором действии, что мы должны разделить?

-Что теперь мы должны сложить?

— Какой же способ мы использовали, чтобы решить это задание?

-Давайте проверим. Правильно ли мы выполнили этот номер. Молодец, все правильно. Садись.

(Один ученик читает)

Работа у доски и в тетрадях.

«Сначала я разложу делимое на разрядные слагаемые» (Пауза) Записывает на доске: 96 = 90 + 6 = 9 дес. + 6

Следующее, что мы должны сделать- это разделить количество единиц делимого на число 3 (Пауза) Записывает на доске: 6 : 3 = 2

Сложим полученные значения частных (Пауза) Записывает на доске: 3 дес. + 2 = 32

«Способом поразрядного деления.»

Самопроверка с доски.

Коммуникативные: умение слушать и понимать речь учителя и одноклассников.

Выражение своих мыслей с достаточной полнотой и точностью.

Аргументация своего мнения и позиции.

Регулятивные: осуществлять контроль и самоконтроль, развитие внимания

Источник