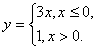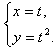Понятия функции способы задания функции элементарные функции

Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ

1.1. Определение функции одной переменной

Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f ( x ) с областью определения X = D( f ) и областью изменения Y = E ( f ). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.

Частным значением функции y = f ( x ) при фиксированном значении аргумента x = x₀ называют y ₀ = f ( x ₀ ).

Графиком функции y = f ( x ) называют геометрическое место точек M ( x ; f ( x )) на плоскости Oxy , где x Î D ( f ) и f ( x ) Î E ( f ).

1.2. Способы задания функции

1) Аналитический способ – способ задания функции с помощью формулы.

Различают несколько способов аналитического задания функции:

а) Функция задана явно формулой y = f ( x ).

Например: 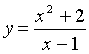, где D( y ) = (– ∞;1) (1;+∞).

б) Функция задана неявно уравнением, связывающем x и y : F( x ; y ) = 0.

Например: – уравнение окружности с центром в начале координат и радиусом r . Если из этого уравнения выразить y через x , то получится две функции:

и ,

которые имеют область определения , а области значений этих функций будут: для первой – , для второй – .

в) Функция задана параметрически с помощью некоторого параметра t , причём и аргумент x , и функция y зависят от этого параметра:

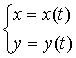
Например: можно задать окружность с помощью параметрических уравнений:

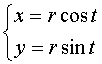
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x , y = cos x и др.

3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.

1.3. Сложная и обратная функции

Определение 1 . Пусть функция y = f ( U) определена на множестве D( f ), а функция U = g ( x ) определена на D( g ), причём E( g ) D( f ).

Тогда функция y = F( x ) = f ( g ( x )) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g ) .

Определение 2 . Пусть задана функция y = f ( x ) взаимно однозначно отображающая множество X = D ( f ) на множество Y = E ( f ). Тогда функция x = g ( y ) называется обратной к функции y = f ( x ), т. е. любому y E( f ) соответствует единственное значение x D ( f ), при котором верно равенство y = f ( x ).

Замечание. Графики функций y = f ( x ) и x = g ( y ) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x , а зависимую y , то графики функций y = f ( x ) и y = g ( x ) будут симметричны относительно биссектрисы первого и третьего координатных углов.

1.4. Элементарные функции

Основные элементарные функции:

y = const ( постоянная функция), D ( y ) = R ; E ( y ) = c .

( линейная функция), D ( y ) = R ; E ( y ) = R .

y = ( степенная функция), α Î R , E( y ), D ( y ) зависят от α .

y = ( показательная функция), a > 0, a ≠ 1, D ( y ) = R , E ( y ) = ( 0; +∞).

y = ( логарифмическая функция) ), a > 0, a ≠ 1, D ( y ) = (0;+∞), E ( y ) = R .

y = sin x , D ( y ) = R , E ( y ) = .

y = cos x, D( y) = R, E( y) = .

y = tg x, D( y) = , E( y) = R.

y = ctg x, D( y) = , E( y) = R.

Обратные тригонометрические функции :

y = arcsin x , D ( y ) = , E ( y ) = .

y = arccos x, D( y) = , E( y) = .

y = arctg x , D ( y ) = R , E ( y ) = .

y = arcctg x , D ( y ) = R , E ( y ) = .

Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.

Например: – элементарная функция.

Графики обратных тригонометрических функций:

Источник

Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 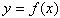, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ — это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .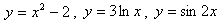

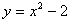
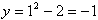
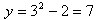
Рассмотрим первый пример — . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

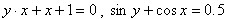
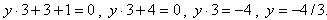
Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

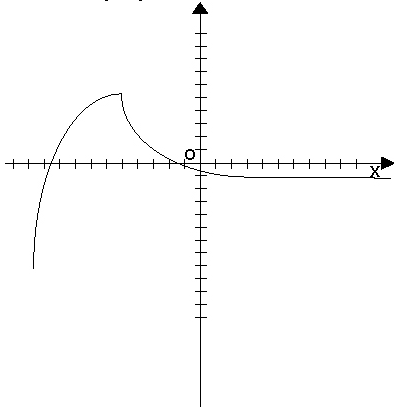
2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 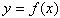. Пример:

3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник