Понятие множества способы задания множеств круги эйлера

Понятие множества и элемента множества. Способы задания множеств. Отношения между двумя множествами и изображение их при помощи кругов Эйлера

Множество – это основное неопределяемое понятие в математике.

– это группа объектов как единое целое.

Обозначение: A, B, C, D, E, …

Множество, не содержащее ни одного объекта, называется пустым и обозначается Ø.

N – мн. натуральных ч.

Q – мн. рациональных ч.

J – мн. иррациональных ч.

R – мн. действительных ч.

Объекты, из которых образовано множество, называются элементами множества.

Обозначение: a, b, c, d, e, …

Множества бывают конечные и бесконечные.

Способы задания множеств.

Множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.

1.Перечисление всех его элементов

2.Использую характеристическое свойство.

Характеристическое свойство – такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

В – множество двузначных чисел.

Если множества заданы перечислением элементов, то достаточно перечислить их общие элементы.

Характеристическое свойство множества А ᴖ В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».

Свойства (ко 2 и 3 вопросу):

Для любых двух множеств А и В справедливо равенство

— А ᴖ В = В ᴖ А — А ᴗ В = В ᴗ А

А ᴖ В = < >А ᴗ В =

В ᴖ А = < >=> А ᴖ В = В ᴖ А В ᴗ А = < >=>А ᴗ В = В ᴗ А

Для любых трех множеств А, В и С справедливо равенство

— (А ᴖ В) ᴖ С = А ᴖ (В ᴖ С) — (А ᴗ В) ᴗ С = А ᴗ (В ᴗ С)

— пересечения относительно объединения — объединения относительно пересечения

(А ᴗ В) ᴖ С = (А ᴖ С) ᴗ (В ᴖ С) (А ᴖ В) ᴗ С = (А ᴗ С) ᴖ (В ᴗ С)

Объединение множеств А и В называется множество, содержащие те и только те элементы, которые принадлежат множеству А или В.

2) В с А => А ᴗ В = А

Если множество, заданное перечислением его элементов, то чтобы получить объединение множеств надо перечислить элементы множества А и добавит из В недостающие элементы.

Если множества заданы указанием характеристического свойства, то используется союз «или».

3. Операции над множествами: разность множеств, дополнение к подмножеству, декартово произведение. Законы этих операций

Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А, но не принадлежат множеству В.

Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В, при условии, что В является подмножеством множества А.

Порядок выполнения действий с множествами:

3-объединение или разность

Доказательства законов с помощью кругов Эйлера.

Декартовым произведением множеств А и В называется множество всех пар 1-ая компонента которых принадлежит множеству А, а 2-ая – множеству В.

Способы задания декартово выражения

2.Указанием характеристического свойства

Читайте также: A) между людьми и между обществом и природой A) научная дисциплина, исследующая и обобщающая специфические связи между обществом и окружающей средой A) Средство организации связи между удаленными абонентами PR: понятие и определение. А) понятие и задачи А- как экономические отношения; АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ В МЕЖДУГОРОДНОМ СООБЩЕНИИ Агентские сети и способы стимулирования их активности Агрессия США во Вьетнаме. Международные последствия вьетнамской войны. Агропромышленная интеграция и кооперация в сельскохозяйственном производстве (значение, понятие, виды)

А \ В
(1;3)	(1;5)
(2;3)	(2;5)
(3;3)	(3;5)

4.При помощи графа

3) Оба множества заданы интервалами 4) Множество А задано несколькими А = [2;5) , B = (4;7] элементами A = <2;4;5>, B = R

5) Множество А – интервал, множество В = R 6)A = R, B = R

1 0 А×В = В×А

2 0 (А×В)×С = А×(В×С) => ассоциативный закон не выполняется

3 0 Дистрибутивный закон декартово произведение относительно объединения

(АᴗВ)×С =

Дистрибутивный закон декартово произведение относительно вычитания

Дата добавления: 2015-04-18 ; просмотров: 47 ; Нарушение авторских прав

Источник

Круги Эйлера — примеры и методы решения логических задач

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

• конечное, например, множество стран;
• бесконечное — множество звёзд во вселенной;
• пустое — множество острых углов в прямоугольнике.

Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.

В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:

• дополнение ¯A в калькуляторе имеет вид A’;
• пересечение A∩B представлено как A intersection B;
• объединение А⋃B обозначено A union B;
• симметрическая разность A∆B — symmetric difference of A and B;
• Относительное дополнение A\B — A\B.

Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

Отношения между понятиями

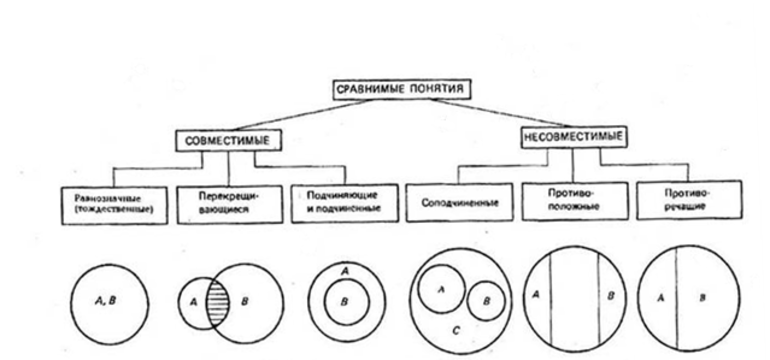
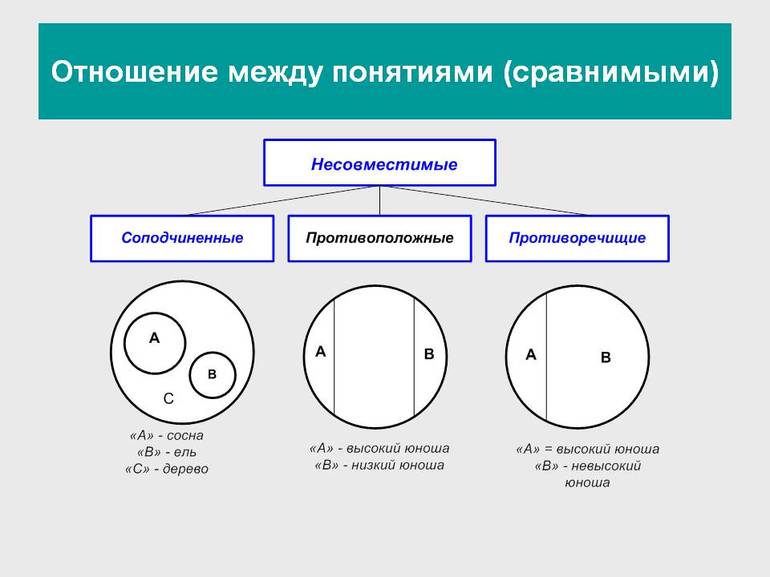
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.

Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

• равнозначные (тождественные);
• перекрещивающиеся;
• подчиняющие и подчинённые.

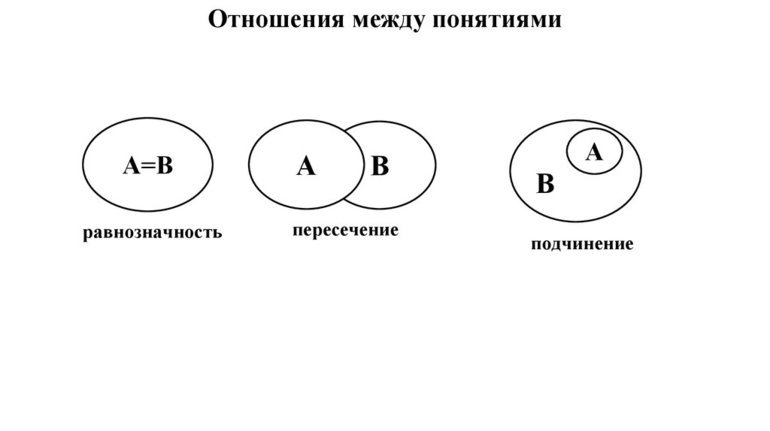
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).

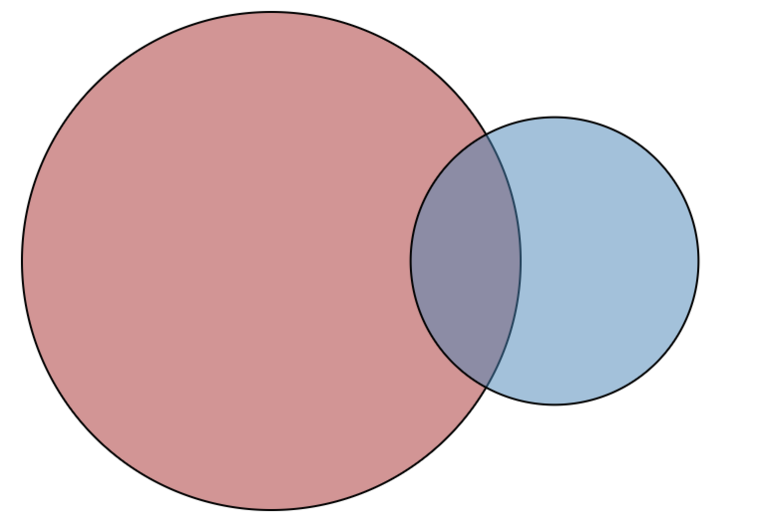
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.

Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».

Несовместимыми называют понятия, не имеющие общих элементов:

• соподчинённые;
• противоположные;
• противоречащие.

Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.

Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).

Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

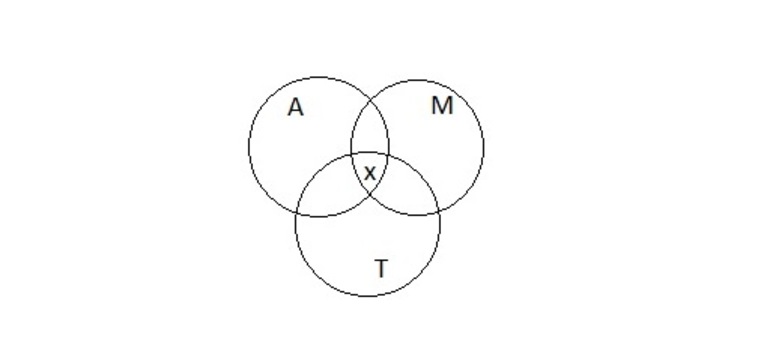
Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

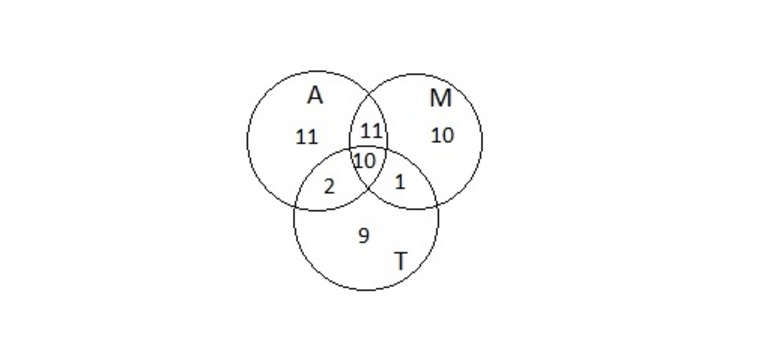
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

Рисунок 3

Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

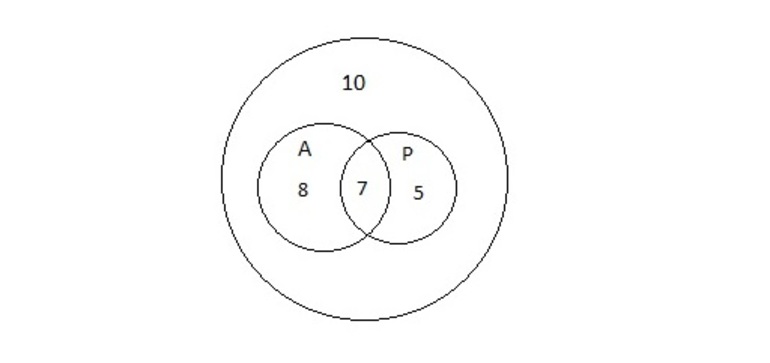
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

Рисунок 4

Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.

Источник

Презентация «Множества. Способы задания. Круги Эйлера»

Описание презентации по отдельным слайдам:

Пр Множества. Способы задания множества. Круги Эйлера. ГБПОУ КК «Краснодарский педагогический колледж» Автор: преподаватель Степанян Л.У.

Биография Леонарда Эйлера. Родился 15 апреля 1707 года. Рано обнаружил математические способности. В 13 лет стал студентом факультета искусств Базельского университета. Проявив интерес к математике, Эйлер привлек к себе внимание. Профессор стал лично руководить занятиями юноши. Историческая справка. Биография

Не забывал Эйлер и другие университетские курсы, по этому и был широко образован. В 17 лет произнёс на латыни речь о сравнении философских воззрений и был удостоен ученой степени магистра. Биография

5 апреля 1727 года Эйлер навсегда покинул родную Швейцарию. Уехал он в Россию, в Петербургскую академию наук, на должность адъюнкта по физиологии. Биография. Эйлер приезжает в Россию.

За первый период пребывания в России (14 лет), он написал более 90 крупных научных работ по математике, гидравлике, архитектуре, навигации, картографии и механике. Петербургская академия по достоинству оценила молодого ученого, в двадцать три года он уже стал профессором физики, а еще через три года Леонард Эйлер получает кафедру высшей математики. Биография. Результаты работы в России

В 1730 – е годы Эйлер становится известен и в Европе. Осенью 1740 внутренняя обстановка в России осложняется. Летом 1741 года Леонард переезжает в Берлин. Однако тесных связей с Петербургской академией наук не прерывает. Вернула Эйлера обратно в Россию, Екатерина II, которая предложила управлять математическим отделением в академии, и звание конференц – секретаря. Биография. Интересный момент.

После 25 лет проживания в Берлине, 60 – летний Эйлер снова возвращается в Россию, в Петербург. К несчастью, после возвращения в Петербург у Эйлера появляется заболевания от которого он перестал видеть. Однако это не отразилось на его работоспособности. Он диктовал свои труды мальчику – портному, который всё записывал по — немецки. Число опубликованных им работ даже возросло. Биография

Круги Эйлера. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Используется в математике, логике, менеджменте и других прикладных направлениях. Круги Эйлера

Множество Множество — совокупность элементов, обладающих некоторым общим свойством, т. е. как единое целое . Множества, состоящие из конечного числа элементов, называют конечными, а остальные множества – бесконечными. Например, множество китов в океане конечно, а множество рациональных чисел бесконечно. Конечное множество может быть задано перечислением его элементов. Понятие множества на примерах

Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N — множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество всех действительных чисел. Основные числовые множества

Над множествами, как и над числами, производят операции. Рассмотрим некоторые из них: пересечение, объединение и разность. Основные операции над множествами

Пересечение множеств Множество, состоящее из элементов, принадлежащих одновременно нескольким множествам Множества А и В называются пересекающимися множествами Определение пересечения

Объединение множеств Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств Операция объединения множеств

Разность множеств это множество всех элементов из А, не являющихся элементами из В Операция разность множеств

КРУГИ ЭЙЛЕРА В ЗАДАЧАХ Алгоритм решения задач 1. Внимательно изучи условия задач. 2. Построй пересечения множеств. 3. Расставь исходные данные. 4. Найдите недостающие данные. 5. Проверь решение. Построение алгоритма для решения задач

1. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое? Условие задача №1

Решение: Решение задачи№1

Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках? Условие задачи №2

Решение: Представление задачи на кругах Эйлера

Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг? Условие задачи №3

Решение: Решение задач

Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу – 8 человек, спортивную школу – 12 человек, музыкальную и художественную школу– 3, художественную и спортивную школу– 2, музыкальную и спортивную школу– 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают? Решение задач

Решение: Решение задачи №3

В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта? Условие задачи №4

Решение задачи №4

Из 100 отдыхающих на турбазе «Графское», 30 детей — отличники учебы, 28 — участники олимпиад, 42 — спортсмены. 8 учащихся одновременно участники олимпиад и спортсмены, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. С колько отдыхающих не относятся ни к одной из групп? Условие задачи № 5

Решение задачи №5

Заключение. Леонард Эйлер жил в 18 веке, но его метод решения целого ряда задач актуален и сегодня, в 21-ом веке. Эйлер использовал идею изображения множеств с помощью кругов. Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы составлением сложных уравнений. Решения задач с громоздкими условиями и со многими данными просты и не требуют особых умозаключений. Применение кругов Эйлера придает задачам наглядность и простоту. Данная тема, расширяет математический кругозор учащихся, обогащает возможности, используемые в решении разнообразных задач. Заключение

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 829 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 296 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 607 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

В презентации изложена биография Леонарда Эйлера — ученого необычайной широты интересов и творческой продуктивности. Он входит в первую пятерку величайших математиков всех времен и народов.Вводится понятие множества, способов задания множества, кругов Эйлера и предлагается решение задач с помощью кругов Эйлера.

Номер материала: ДБ-857048

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В российских школах оборудуют кабинеты для сообщества «Большой перемены»

Время чтения: 1 минута

Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник