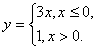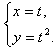Понятие функции. Способы задания функции



Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Определение. Отображения 
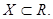
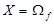
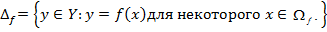
Определение. Если каждому элементу х множества X ( 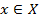
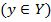
y = f(x), y = F(x) — функциональная зависимость х и у.
f, F — характеристики функции, х — независимая переменная (аргумент),
у — зависимая переменная.
Рассматривают три способа задания функции: аналитический, табличный и графический.
Способ задания функции при помощи формулы называется аналитическим.Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции .
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции .
Функция у = f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями
Классификация функций.
Элементарные функции разделяют на алгебраические и неалгебраические (трансцендентные).
Алгебраической называют функцию, в которой над аргументом производится конечное число алгебраических действий.
К ним относятся:
— целая рациональная функция (многочлен, полином)
— дробно-рациональная функция – отношение двух многочленов
— иррациональная функция (среди действий над аргументом есть извлечение корня).
К трансцендентным относятся: показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Четные и нечетные функции.
Функция у = f(х) называется четной или нечетной, если она определена на множестве симметричном относительно нулевой точки и обладает на нем свойством f(-x)=f(x) или свойством f(-x) = -f(x). В противном случае функцией общего вида. График четной функции симметричен относительно оси ординат, график нечетной симметричен относительно начала координат.
Произведения двух четных или двух нечетных функций есть функция четная, произведения четной функции на нечетную есть нечетная функция
Монотонные функции.
Пусть (a,b) промежуток с концами в точках a и b, где a
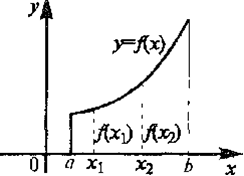
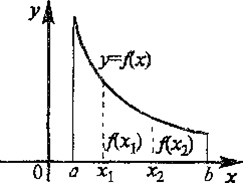
Функция у = f(х) называется возрастающей (убывающей) на промежутке (a,b), если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 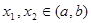
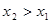
Тогда функция возрастает на промежутке X, если 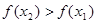
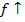
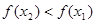
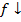
Запись 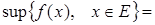
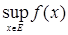
Функции возрастающие и убывающие называется монотонными. К монотонным функциям относятся также неубывающие и невозрастающие функции.
Ограниченные функции.
Функция называется ограниченной на промежутке (a,b), если 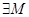
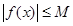
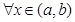
В противном случае функция называется неограниченной.
Периодическая функция.
Функция называется периодической с периодом 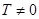
Источник
Функция. Способы задания функций.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.
3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.
4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
При разложении числа Эйлера задается функцией:
Ее сокращение приведено ниже:
При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.
Источник
Понятие функции. Способы задания функции
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 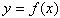
Существуют разные способы задания функций.
1. Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например 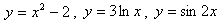
Рассмотрим первый пример — 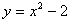
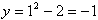
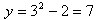
Функция может быть задана на разных частях множества X разными функциями.
Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например 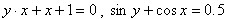
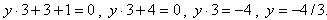
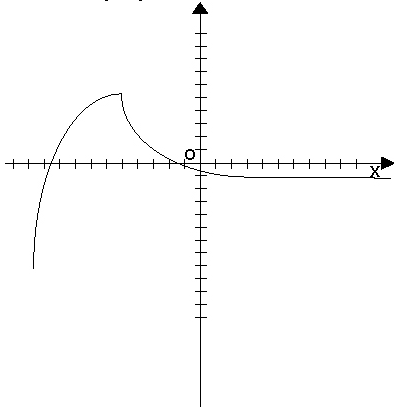
При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,
Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 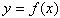
3. Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Ошибка в тексте? Выдели её мышкой и нажми 
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Источник