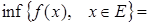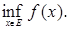Понятие функции. Способы задания функции



Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Определение. Отображения 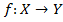
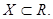
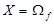
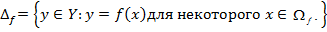
Определение. Если каждому элементу х множества X ( 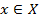
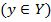
y = f(x), y = F(x) — функциональная зависимость х и у.
f, F — характеристики функции, х — независимая переменная (аргумент),
у — зависимая переменная.
Рассматривают три способа задания функции: аналитический, табличный и графический.
Способ задания функции при помощи формулы называется аналитическим.Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции .
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции .
Функция у = f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями
Классификация функций.
Элементарные функции разделяют на алгебраические и неалгебраические (трансцендентные).
Алгебраической называют функцию, в которой над аргументом производится конечное число алгебраических действий.
К ним относятся:
— целая рациональная функция (многочлен, полином)
— дробно-рациональная функция – отношение двух многочленов
— иррациональная функция (среди действий над аргументом есть извлечение корня).
К трансцендентным относятся: показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Четные и нечетные функции.
Функция у = f(х) называется четной или нечетной, если она определена на множестве симметричном относительно нулевой точки и обладает на нем свойством f(-x)=f(x) или свойством f(-x) = -f(x). В противном случае функцией общего вида. График четной функции симметричен относительно оси ординат, график нечетной симметричен относительно начала координат.
Произведения двух четных или двух нечетных функций есть функция четная, произведения четной функции на нечетную есть нечетная функция
Монотонные функции.
Пусть (a,b) промежуток с концами в точках a и b, где a
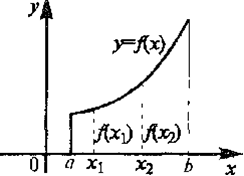
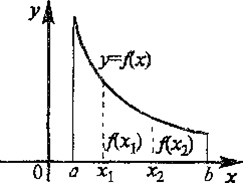
Функция у = f(х) называется возрастающей (убывающей) на промежутке (a,b), если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 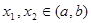
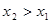
Тогда функция возрастает на промежутке X, если 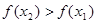
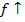
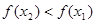
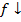
Запись 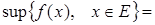
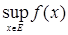
Функции возрастающие и убывающие называется монотонными. К монотонным функциям относятся также неубывающие и невозрастающие функции.
Ограниченные функции.
Функция называется ограниченной на промежутке (a,b), если 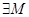
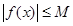
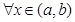
В противном случае функция называется неограниченной.
Периодическая функция.
Функция называется периодической с периодом 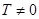
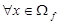
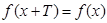
Источник
2. Определение, способы задания и свойства функции
Определение:Если каждому элементухмножестваХпо какому-либо законуf(или по определенному правилуf) ставится в соответствие единственный элементуиз множестваУ, то говорят, что заданафункциональная зависимостьуотх по законуy=f(x)илифункция y=f(x).
При этом х называетсянезависимой переменной(илиаргументом),у – зависимой переменной(илизначением функции). МножествоХназываетсяобластью определения( илиобластью существования) функции и обозначаетсяD(f), множествоУназываетсяобластью значений функции и обозначаетсяЕ(f).
Если множество Хне оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменнойх, при котом формула имеет смысл. Например, для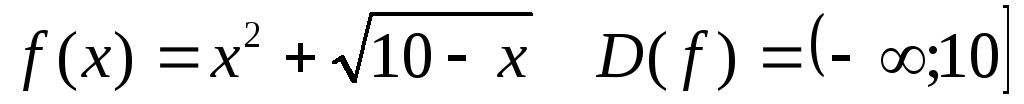
Задать функцию– значит, указать законfили правило, позволяющее, знаях.находить соответствующее значениеу.
1. Аналитический– если функция задана с помощью формулы. Наиболее удобный способ для математического анализа, позволяющий исследовать функцию.
2. Табличный– если задана таблица значений функции, соответствующих определенным значением аргумента. Этот способ имеет широкое применение в экономике: экспериментальные измерения, таблицах бухгалтерской отчетности, банковской деятельности, статистических данных и т.п.
3. Графический– если задан график. Этот способ обычно используется с употреблением самопишущих приборов (осциллографы, сейсмографы и т.п.). В экономике используются графики, характеризующие динамику экономических параметров: объема ВВП, выручки, курсы валют, курса акций и т.п.
4. Словесный– если функция описывается правилом, составления, например, функция Дирихле:f(x)=1 , если x – рационально и f(x)=0, если x— иррационально.
1. Четность и нечетность
При этом D(f)называетсясимметричнойотносительно О(0;0). График четной функции симметричен относительно Оу, а график нечетной – относительно О(0;0).
Функция называется возрастающейна промежуткеID(f), если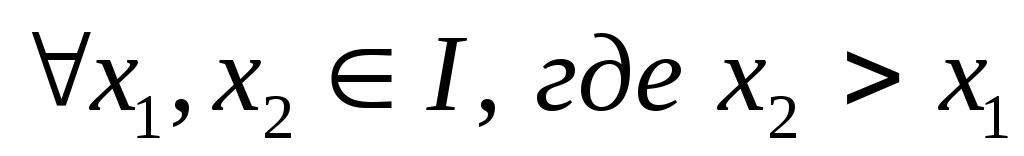
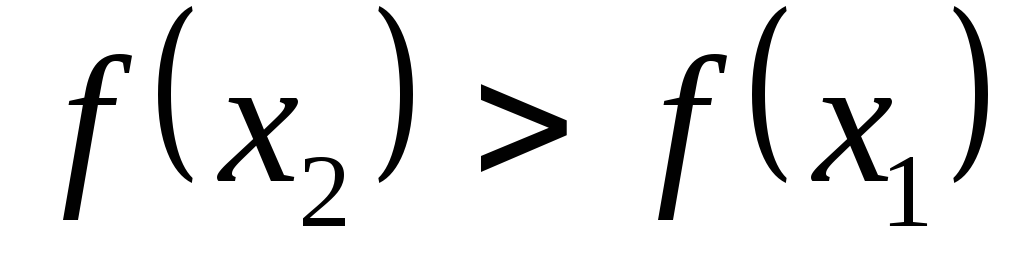
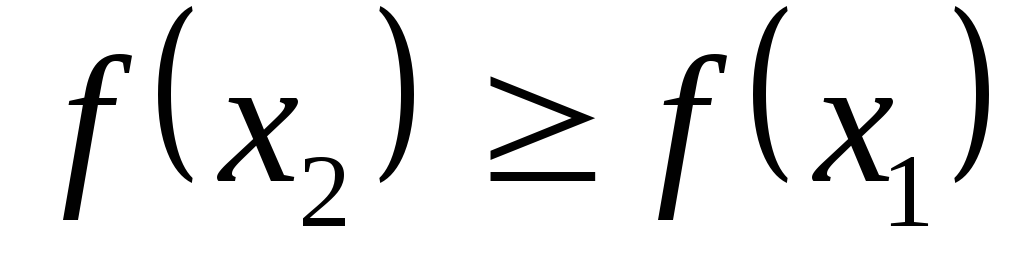
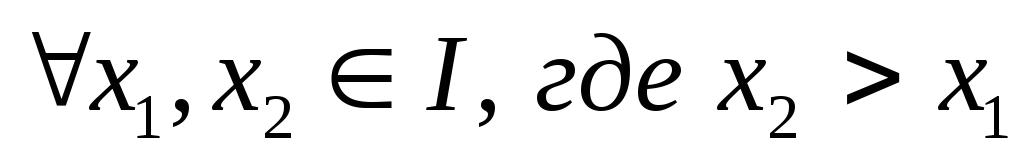
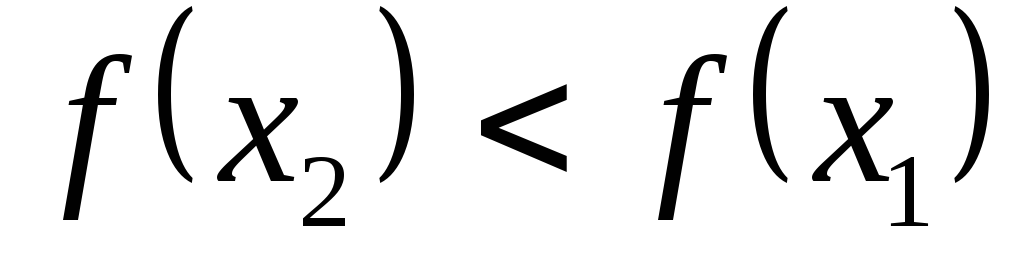
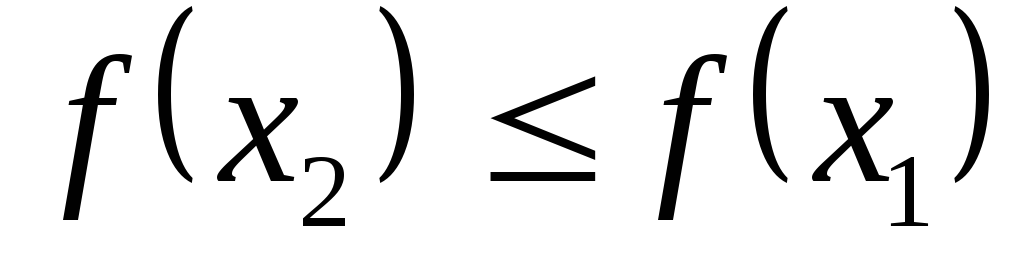
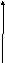
Возрастающие, неубывающие, убывающие и невозрастающие функции на промежутке ID(f)называютсямонотоннымина этом промежутке, а возрастающие и убывающие –строго монотонными.
Функция называется ограниченнойна множествеD(f), если существует такое число М>0, чтохD(f)выполняется неравенство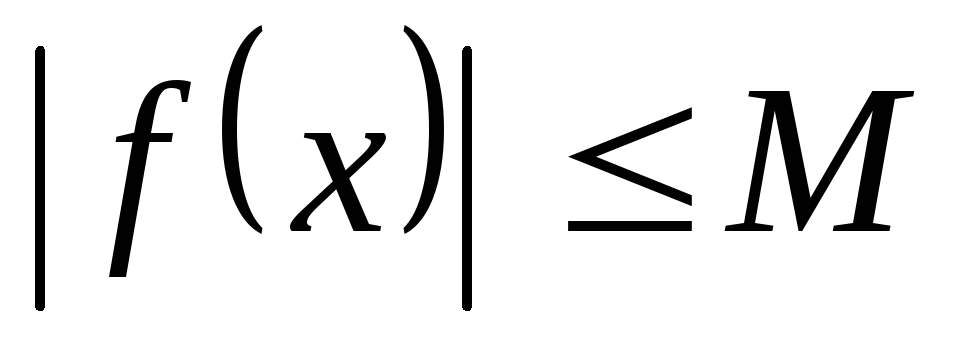
если 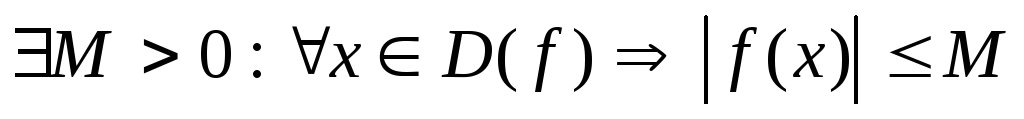
Графики таких функций ограничены прямыми 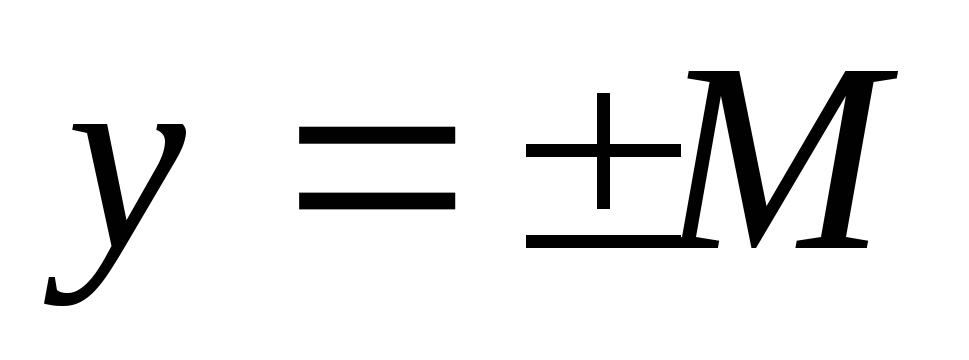
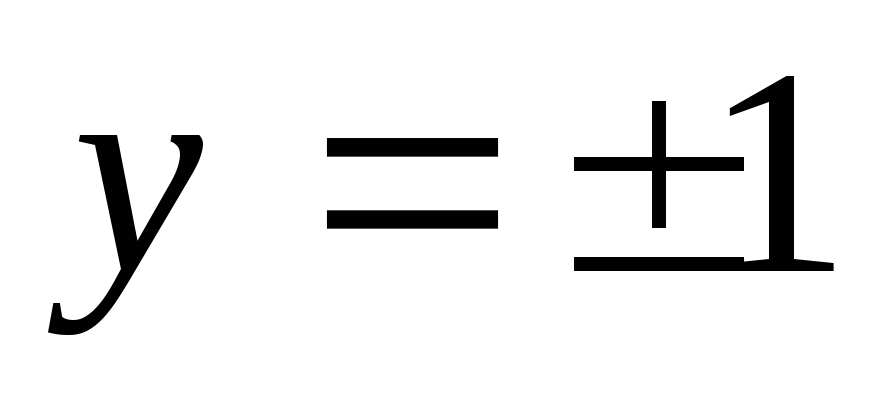
Число Т называется периодомфункции. Если Т – период, тоnTтакже является периодом, гдеn=±1;±2;…
Например, функция у=sin x является периодической, т.к.xD(f) sin(x+2π)=sin x. Аналогично можно доказать, что ±2π; ±4π; ±6π;… также являются периодами. Период 2π являетсянаименьшим положительными называетсяосновным.
Применение функций в экономике
Функции находят широкое применение в экономической теории и практике. Наиболее часто используются следующие функции:
1.Функция полезности (функция предпочтений) – зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.
2.Производственная функция зависимость результата производственной деятельности от обусловивших его факторов.
3.Функция выпуска (частный вид производственной функции) – зависимость объёма производства от наличия или потребления ресурсов.
4.Функция издержек (частный вид производственной функции) –зависимость издержек производства от объёма продукции.
5.Функция спроса, потребления и предложения – зависимость объёма спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).
Например, исследуя зависимости спроса на различные товары от дохода можно установить уровни доходов 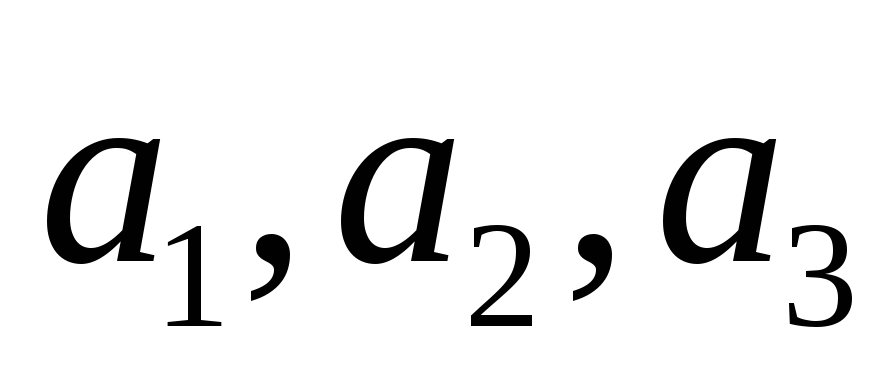
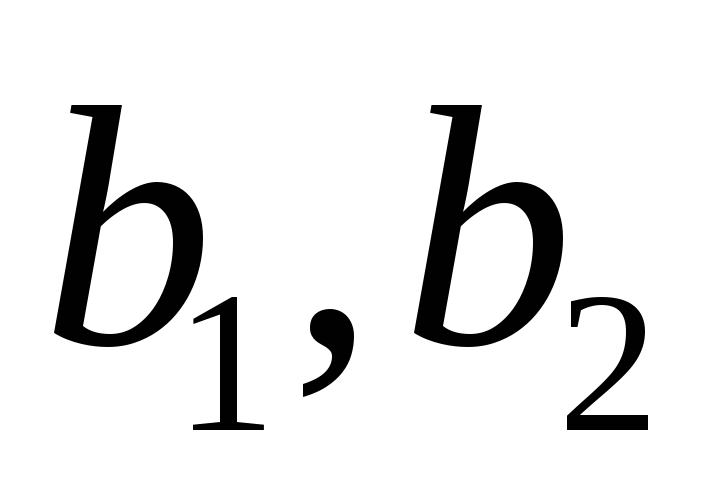
Рассматривая в одной системе координат кривые спроса и предложения, можно установить равновесную (рыночную) цену данного товара в процессе формирования цен в условиях конкурентного рынка (паутинообразная модель) (см. рис.2)
Изучая в теории потребительского спроса кривые безразличия (линии, вдоль которых полезность двух благ х и у одна и та же), например, задаваемые в виде xy=U, и линию бюджетного ограничения 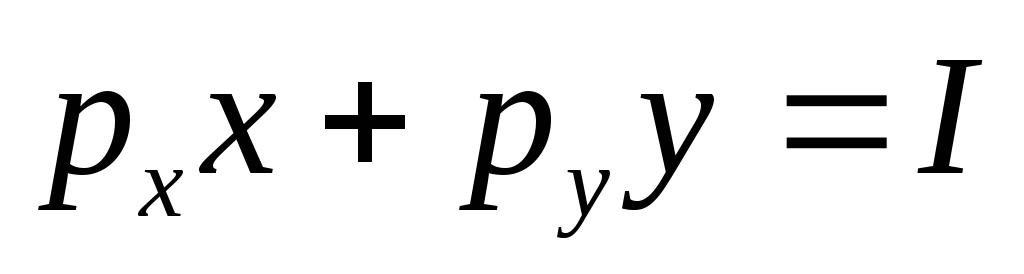
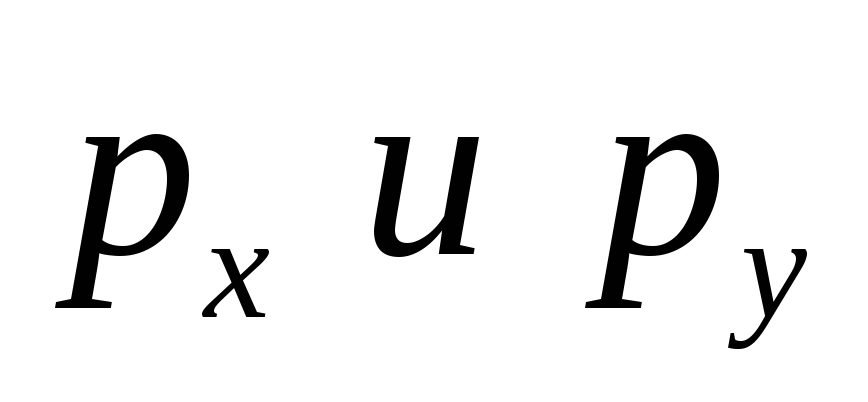
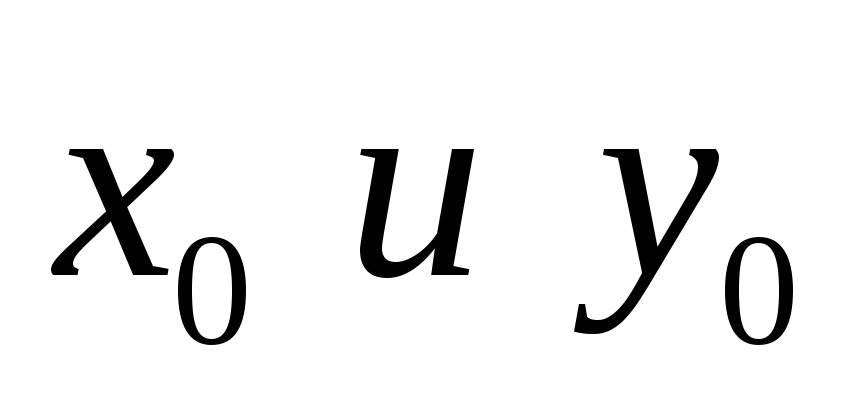
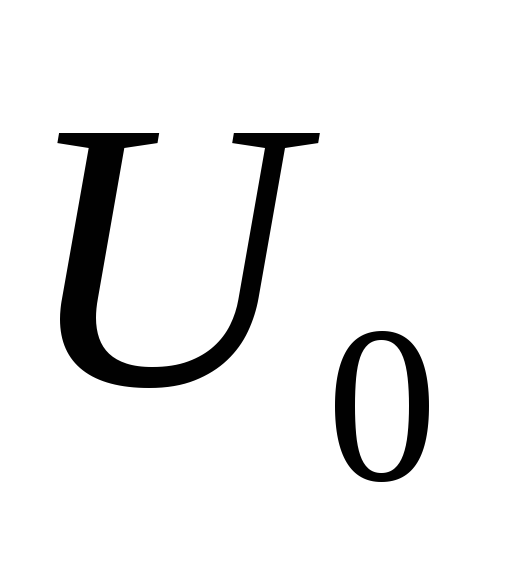
Товары 2-ой необходимости
Товары 1-ой необходимости
Рассматривая функции издержек (полных затрат) с(q) и дохода фирмы r(q), мы можем установить зависимость прибыли π(q)=c(q)-r(q) от объёма производства q (см. рис.4) и выявить уровни объёма производства, при которых производство продукции убыточно (0 2 / 4 2 3 4 > Следующая > >>
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник