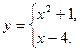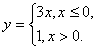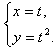Понятие функции область определения способ задания

Понятие функции. Область её определения. Способы задания

К понятию функции приводит изучение разнообразных явлений в окружающем нас мире. Например, каждому значению длины грани куба соответствует его объём; каждому моменту времени в данной местности соответствует определённая температура воздуха; каждому значению возраста животного соответствует его масса; каждому показателю рентабельности соответствует определённая величина прибыли.

Во всех этих примерах общим является то, что каждому числовому значению одной величины сопоставляется определенное числовое значение другой.

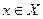
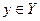
Правило f , сопоставляющее каждому числу единственное число , называетсячисловой функцией, заданной на множестве X и принимающей значения во множестве Y.

Если 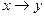, то пишут y = f(x).

Функцией называют также уравнение y = f(x), т.е. формулу, где у выражено через х с помощью правила f.

В уравнении y = f(x) «х» называют независимой переменной или аргументом, а у — зависимой переменной или функциейот «х». Зависимость х и у называется функциональной.

Множество всех значений независимой переменой, для которых определена функция, называетсяобластью определенияэтой функции,обозначается D(f).

Обычно D(f) представляет собой интервал – открытый, полуоткрытый, бесконечный, или их сумму.

Пример. 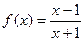. Найти D(f).

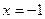
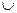
Решение. Функция не определена при . D(f) = (-∞, -1) (-1, +∞).

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ: функция задаётся в виде одной или нескольких формул или уравнений.

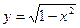
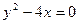
Например, 1) , 2) , 3)

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию.

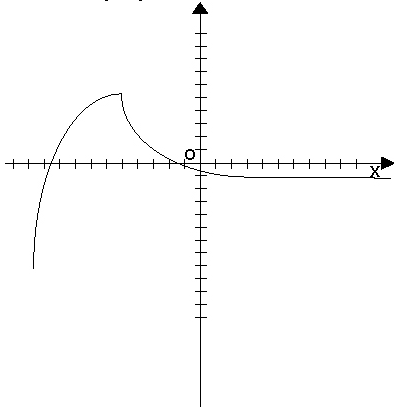
Графический способ: задаётся график функции.

Совокупность точек плоскости xOy, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции, называется графикомданной функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Преимущество графического задания является его наглядность, недостатком – его неточность.

Табличный способ: функция задаётся таблицей ряда значений аргумента и соответствующих значений функции.

Например, таблицы тригонометрических функций, логарифмов, таблицы железнодорожных тарифов.

Табличный способ удобен для использования, он широко применяется при регистрации опытов, лабораторных анализов, при подсчете объема грубых кормов в скирдах и т. д. К недостатку способа относится то, что представление о функциональной зависимости здесь не является полным, так как невозможно поместить в таблице все значения аргумента.

Существует еще один способ задания функции, возникший с развитием и внедрением в производство ЭВМ. Этот способ состоит в указании программы для вычисления значения функций на ЭВМ.

Источник

Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 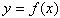, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ — это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .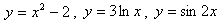

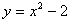
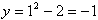
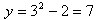
Рассмотрим первый пример — . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

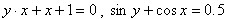
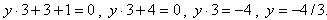
Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 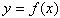. Пример:

3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник

Определение функции и способы ее задания

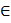
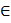
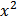
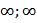
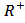
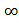
(Определение: Пусть X и Y – числовые множества. Если каждому элементу x X по некоторому правилу f поставлен в соответствие единственный элемент y Y, то говорят, что на множестве X определена функция y=f(x). x=D(f) – область значения; y= ; x=(- )=R; E(f)= =[0;+ )

способы задания: 1) Аналитический способ(формулой); 2) Графический способ(график); 3) Табличный способ; 4) Словесное описание.)

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная

Способы задания функций

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Источник

Реферат: Понятие функции. Область определения функции. Способы задания функции

ИНСТИТУТ БИЗНЕСА, ПРАВА И ИНФОРМАЦИОННЫХ

Понятие функции. Область определения функции.

Способы задания функции

Выполнил: Мальский Эдуард Александрович,

студент 2 курса

контрольной работы по дисциплине «Математика»

на тему «Понятие функции. Область определения функции.

Способы задания функции»

2. Способы задания функции…………………………………………. 5

3. Виды функций и их свойства……………………………………………. 6

Список использованной литературы…………………………………………. 12

Функция — одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r 2 . Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции — теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Раздел 1. Функция и её свойства.

Функция- зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у .

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у , соответствующее заданному значению х .

Область определения функции- все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х из области определения функции выполняется равенство f ( x )= f (- x )

Функция является нечетной- если для любого х из области определения функции выполняется равенство f (- x )=- f ( x )

Раздел 2. Способы задания функции.

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у= f ( x ) , где f ( x )- с переменной х . В таком случае говорят, что функция задана формулой или что функция задана аналитически.

На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Раздел 2. Виды функций и их свойства.

1) Постоянная функция- функция, заданная формулой у= b , где b — некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у= kx , где к¹0. Число k называется коэффициентом пропорциональности .

Cвойства функции y=kx :

1. Область определения функции- множество всех действительных чисел

2. y=kx — нечетная функция

3. При k>0 функция возрастает, а при k 0функция возрастает, а при k 0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k 2

Свойства функции y=x 2 :

1. Область определения- вся числовая прямая

2. y=x 2 — четная функция

3. На промежутке [0;+¥) функция возрастает

4. На промежутке (-¥;0] функция убывает

Графиком функции является парабола .

Свойства функции y=x 3 :

1. Область определения- вся числовая прямая

2. y=x 3 — нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой y = x n , где n — натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x 2 ; y=x 3 . Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8. В этом случае функция y = x n обладает теми же свойствами, что и функция y=x 2 . График функции напоминает параболу y=x 2 , только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х| n обладает теми же свойствами, что и функция y=x 3 . График функции напоминает кубическую параболу.

8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y = x — n , где n — натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.

Пусть n- нечетное число, большее единицы: 3,5,7. В этом случае функция y = x — n обладает в основном теми же свойствами, что и функция y=1/х.

Пусть n- четное число, например n=2.

Свойства функции y=x -2 :

1. Функция определена при всех x¹0

2. y=x -2 — четная функция

3. Функция убывает на (0;+¥) и возрастает на (-¥;0).

Теми же свойствами обладают любые функции при четном n, большем двух.

1. Область определения — луч [0;+¥).

2. Функция y= Ö х — общего вида

3. Функция возрастает на луче [0;+¥).

1. Область определения- вся числовая прямая

3. Функция возрастает на всей числовой прямой.

При четном n функция обладает теми же свойствами, что и функция y = Ö х . При нечетном n функция y = n Ö х обладает теми же свойствами, что и функция y = 3 Ö х.

12)Степенная функция с положительным дробным показателем- функция, заданная формулой y = x r , где r — положительная несократимая дробь.

Свойства функции y=x r :

1. Область определения- луч [0;+¥).

2. Функция общего вида

3. Функция возрастает на [0;+¥).

На рисунке изображен график функции y=x 5/2 . Он заключен между графиками функций y=x 2 и y=x 3 , заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y = x r , где r>1.

На рисунке изображен график функции y=x 2/3 . Подобный вид имеет график любой степенной функции y = x r , где 0 — r , где r — положительная несократимая дробь.

1. Обл. определения -промежуток (0;+¥)

2. Функция общего вида

3. Функция убывает на (0;+¥)

Если функция y = f ( x ) такова, что для любого ее значения y_o уравнениеf ( x )= y_o имеет относительно х единственный корень, то говорят, что функция f обратима.

Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.

Таким образом, чтобы построить график функции, обратной к функции y=f(x), надо график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x.

15)Сложная функция- функция, аргументом которой является другая любая функция.

Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.

Понятие фу нкции является одним из ос новных понят ии ма­ тематики вообще . Оно не воз никло сразу в таком виде, как мы им пользуемс я сейчас, а как и другие фундаментальные понятия прошло длинный пут ь диа­лектического и и сторического развития. Идея функциональной зависимости восходит к древнегре­ чес кой математике.

Впервые термин «функция» вводит в рассмотрение знаменитый немецкий математик и философ Лейбниц в 1694 г. Однако, этот термин /определения он не дал вообще/ он употребляет в узком смысле, понимая под функцией изменение ординаты кривой в зависимости от изменения ее абсциссы. Таким образом, понятие функции носит у него «геометрический налет».

Ученик Лейбница Иоганн Бернулли пошел дальше своего учителя. Он дает более общее определение функции, освобождая последнее от геометрических представлений и терминов: «функцией переменной величины называется количество, образованное каким угодно способом из этой величины и постоянных».

Список использованной литературы

в контрольной работе по дисциплине «Математика»

на тему «Понятие функции. Область определения функции. Способы задания функции»

1. Евстафьева В.Ю. Математика. Алгебра. Функции. Анализ данных. Москва: «Дрофа», 2000 года.

2. Ильин В.А., Куркина А.В. Высшая математика. Москва: «Проспект», 2003 года.

3.Колмогоров А. Н. Алгебра и начала анализа. Москва: «Просвещение», 1990 года.

4. Максименко В.Н. Математический анализ в примерах и задачах: Часть. 2. Москва: «НГТУ», 2002 года.

5. Никольский С.Н. Курс математического анализа, учебник. Москва: «Физматлит», 2002 года.

Источник

Название: Понятие функции. Область определения функции. Способы задания функции Раздел: Рефераты по математике Тип: реферат Добавлен 17:58:55 31 мая 2011 Похожие работы Просмотров: 4417 Комментариев: 21 Оценило: 12 человек Средний балл: 4.2 Оценка: 4 Скачать