Понятие функции область определения функции способы задания функции 7 класс

Дидактические материалы для занятий математического кружка «Математика +» 7 класс. Занятие21. Понятие функции. Способы задания функции
план-конспект занятия по математике (7 класс) на тему

Математический кружок- одна из наиболее эффективных форм внеклассных занятий. Для меня, как учителя, важно иметь под рукой пособие, в котором представлены идеи решений и которое позволило бы провести цикл занятий математического кружка не прилагая титанических усилий для подбора материала. Мной предпринята попытка составления такой разработки, которую можно было использовать при подготовке к занятиям.

Скачать:

Вложение	Размер
zanyatie_21._ponyaie_funktsii._sposoby_zadaniya_funktsii.docx	95.49 КБ

Предварительный просмотр:

Понятие функции одной переменной

Рассмотрим два числовых множества X и Y . Правило f , по которому каждому числу х ∈ Х ставится в соответствие единственное число y ∈ Y , называется числовой функцией , заданной на множестве Х и принимающей значения во множестве Y .

Таким образом, задать функцию, значит задать три объекта:

1) множество Х (область определения функции);

2) множество Y (область значений функции);

3) правило соответствия f (сама функция).

Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x 3 . В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y , пишут y = f(x). Здесь » х » называют независимой переменной или аргументом , а » y » — зависимой переменной (т.к. выражение типа x 3 само по себе не имеет определенного числового значения пока не указано значение х ) или функцией от х . О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у . Например, если х=2 , то функция f(x) =x 3 принимает значение у = f(2) =2 3 =8 .

Подведем итог:

Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией , если каждому значению x соответствует единственное значение y .

Переменную x называют независимой переменной или аргументом , а переменную y — зависимой. Говорят, что y является функцией от x . Значение y , соответствующее заданному значению x , называют значением функции .

Все значения, которые принимает x , образуют область определения функции ; все значения, которые принимает y , образуют множество значений функции .

D(f) — значения аргумента. E(f) — значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.

Графиком функции называется множество всех точек на координатной плоскости , абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Если некоторому значению x=x 0 соответствуют несколько значений (а не одно) y , то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.

Способы задания функции одной переменной

Существуют несколько способов задания функции.

Аналитический способ. Функция f задается в виде формулы y=f(x). Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например y=3x+2x 2 . Здесь значению x = 1 соответствует y=3∙1+2∙1 2 =5 , значению x=2 соответствует y=3∙2+2∙2 2 =6+8=14 и т. д.

Функция может быть задана на разных частях множества X разными функциями. Например:

Чем хорош аналитический способ задания функции? Тем, что если у вас есть формула — вы знаете про функцию всё! Вы можете составить табличку. Построить график. Исследовать эту функцию по полной программе. Точно предсказать, где и как будет вести себя эта функция. Но в исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.

Табличный способ . Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x) , соответствующие каждому х . Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.

Источник

Понятие функции

Урок 12. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие функции»

· ввести понятия «функциональная зависимость»;

· узнать о способах задания функции;

· познакомиться с историей функции.

Изучение темы начнём с рассмотрения нескольких примеров.

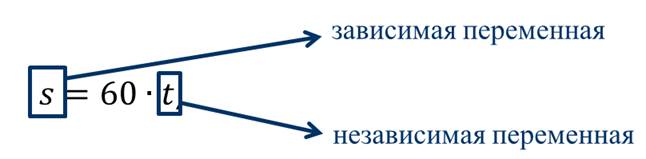
В рассмотренном примере переменную t называют независимой переменной, так как её значения мы выбирали произвольно. А переменную s называют зависимой переменной, так как её значения определяются выбранными значениями переменной t.

Давайте рассмотрим ещё один пример.

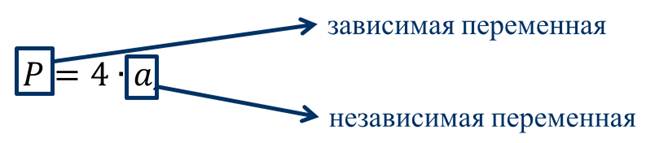
В этом примере переменная а является независимой переменной, а переменная Р – зависимой переменной.

В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называю функциональной зависимостью или функцией.

Независимую переменную называют также аргументом, а зависимую – функцией от этого аргумента.

Так в рассмотренных примерах путь, пройденный автомобилем, является функцией от времени движения автомобиля. А периметр квадрата является функцией от его стороны.

Значения, которые принимает независимая переменная, образуют область определения функции.

Все значения зависимой переменной называют значениями функции.

А сейчас выполним следующее упражнение.

В семнадцатом веке французские математики Рене Декарт и Пьер Ферма впервые начали выражать зависимость между переменными при помощи формулы.

В рассмотренных выше примерах функции задавались с помощью формулы. И этот способ задания функции является более распространённым. Но давайте рассмотрим ещё несколько примеров.

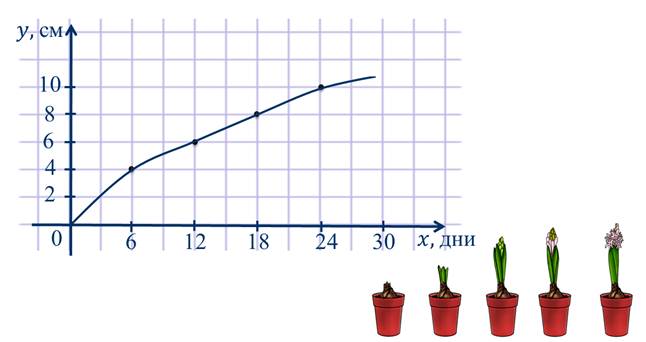
На рисунке показано, как изменялась высота гиацинта в зависимости от его возраста. Рост указан в сантиметрах, а его возраст в днях.

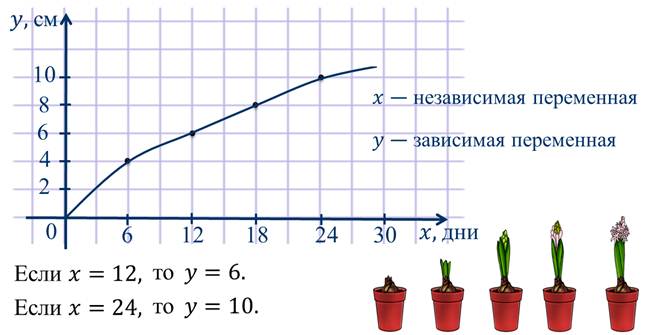
С помощью этого графика мы можем сказать, какую высоту имеет цветок в зависимости от его возраста. Например,

В данном случае икс является независимой переменной, а игрек – зависимой переменной.

Здесь зависимость одной переменной от другой также является функциональной зависимостью, или функцией. Но, в отличие от предыдущих примеров, функция задана в виде графика.

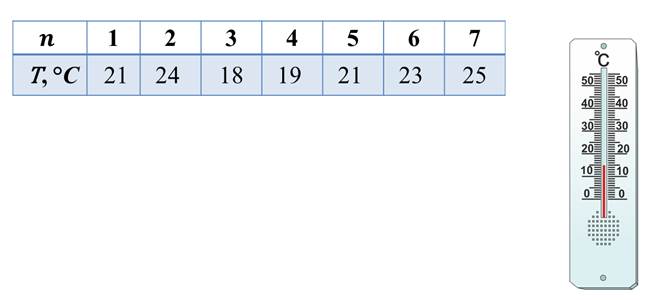
И рассмотрим таблицу, в которой представлен результат измерений средней температуры воздуха в комнате в течение недели.

В данной таблице каждому значению n (то есть номеру дня недели) соответствует значение t (температуры воздуха в комнате). Например,

Здесь каждому значению независимой переменной соответствует единственное значение зависимой переменной.

А такую зависимость мы называем функцией. В этом примере функция задана в виде таблицы.

Источник

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Методическая разработка урока алгебры в 7-м классе на этапе введения понятия функции

Разделы: Математика

Цели урока:

• В направлении личностного развития: воспитание качеств личности, обеспечивающих культуру речи, социальную мобильность, способность принимать самостоятельные решения, развитие способности к умственному эксперименту, необходимых для адаптации в современном информационном обществе.
• В метапредметном направлении: развитие мотивов и интересов познавательной деятельности учащихся; формирование умения планировать маршруты достижения цели, навыков самоконтроля и самооценки, умений классифицировать и обобщать.
• В предметном направлении: овладение начальными функциональными понятиями; формирование представлений о математике как о методе познания окружающей действительности, умений чётко и грамотно выражать свои мысли с применением математической терминологии.

Задачи урока:

• В направлении личностного развития. Показать учащимся взаимосвязь реальных жизненных ситуаций с современными науками, в том числе с математикой. Развивать коммуникативную компетентность учащихся в процессе общения в группе, при организации сотрудничества как со сверстниками, так и с учителем. Учить объективной оценке как своей деятельности, так и других. Показать тесную связь обучения с непосредственными жизненными потребностями, интересами и социокультурным опытом учащихся.
• В метапредметном направлении. Добиться в каждыймомент урока у ученика понимания того, какими способами он достиг нового знания и какими способами ему нужно овладеть, чтобы узнать то, чего он еще не знает. Учить сравнивать, анализировать, обобщать, выделять существенное, выдвигать гипотезу и подтверждать или опровергать ее. Показать возможность применения новых знаний для исследования различных процессов как в окружающем нас мире, так и в других науках, акцентируя внимание на том, что новые знания важны и актуальны. Показать возможность применения на уроках математики знаний, полученных в других предметных областях.
• В предметном направлении. Ввести понятие функции, независимой и зависимой переменных, понятие однозначности. Научить выделять существенные признаки нового знания, использовать полученные знания при анализе конкретных ситуаций. Ввести новую математическую символику и научить учащихся пользоваться ей при описании математических моделей и решении задач.

Учебные материалы урока. Учебник: Алгебра: 7 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вента-Граф, 2015г.

Раздаточные материалы: листы с оформленным домашним заданием у каждого ученика , опорные карточки на каждого ученика , карточки с задачами оформленные на группу , оценочные листы на каждого ученика .

Техническое оснащение: компьютер, интерактивная доска, презентация к уроку .

План урока.

1 Организационный момент. Мотивация к учебной деятельности. – 2 минуты.

2 Проверка домашнего задания – 3 минуты.

3 Актуализация опорных знаний. Открытие нового знания. Формулирование темы урока. – 10 минут.

4 Введение новой математической символики. Первичное применение нового знания. – 10 минут.

5 Проблемная ситуация. Мотивация к дальнейшему изучению нового знания. – 10 минут.

6 Подведение итогов. Составление плана по дальнейшему изучению нового понятия. Рефлексия. Домашнее задание. – 10 минут.

Описание основных этапов урока

1. Организационный момент. Мотивация к учебной деятельности. 2 минуты.

Цель: включение учащихся в деятельность на личностно-значимом уровне. «Хочу, потому что могу».

Деятельность учителя и ученика.

На доске выписаны операторы для постановки вопросов: «КТО? ЧТО? ЗАЧЕМ? КАК? ЧЕМ? КАКИЕ? КОГДА?», создающие интригующее начало урока и неподдельный интерес учеников, что способствует включению их в деловой ритм, возникает положительная эмоциональная направленность. Учитель сообщает ученикам, что сегодня на уроке мы будем исследовать процессы в окружающем нас мире, а умение задавать вопросы необходимо для любого исследователя, поэтому в конце урока, подводя итоги, мы будем формулировать и отвечать на вопросы. Учитель произносит сообщение доброжелательным тоном и начинает с приветствия.

Учитель. Многие науки исследуют процессы в которых присутствуют переменные величины, и математика, как царица всех наук, изучая их находит связи между переменными. Часто, если не ежедневно, мы слышим прогноз погоды. Какими величинами характеризуется погода за окном? Меняются эти величины или нет? От чего это зависит?

Ученики. Погода за окном характеризуется температурой, атмосферным давлением, направлением ветра и т.д. Величины меняются в зависимости от времени года, времени суток.

Учитель просит привести примеры процессов, в которых величины меняют свое значение, и ученики отвечают: «Движение автомобиля с разной скоростью, рост человека, стоимость покупки и т.д.». Обсуждается один из примеров, учитель задает вопросы: «Какими величинами характеризуется этот процесс? Как величины меняются? От чего это зависит?» В ходе беседы выясняется, что стоимость покупки характеризуется ценой единицы товара, количеством денег у покупателя, количеством возможных единиц товара для покупки.

2. Проверка домашнего задания.

Цель: повторение изученного материала в курсах математики 5-6 классов УМК А.Г.Мерзляка, которые носят функциональный пропедевтический характер.

Деятельность учителя и ученика.

При проверке домашнего задания класс делится на 4 группы (по количеству домашних задач), в каждой группе учитель назначает консультантов, которые будут координировать действия всех членов группы. Домашнее задание , оформлено на листах формата А4 на каждого ученика.

Задача 1. В цистерне было 740 л воды. Каждый час из нее вытекает 20 л. Составьте формулу для вычисления объема воды, которая осталась в цистерне через t часов, обозначив объем оставшейся воды V(t) (читается «в» от «т»). Вычислите этот объем, если t=2; t=6; t=10. В какой момент времени в цистерне не останется воды? Данные вычислений занесите в таблицу .

Задача 2. В романе Жюль Верна «Дети капитана Гранта» читаем: «Погода стояла прекрасная, не слишком жаркая… Роберт узнал, что средняя годовая температура в провинции Виктория +74º по Фаренгейту». Сколько же это будет в привычных для нас градусах Цельсия? Формула для вычисления температуры в градусах Цельсия по температуре в градусах Фаренгейту выглядит так: . Используя формулу заполните таблицу .

В пустых клетках таблицы придумайте свое значение tº C и найдите соответствующее ему значение Fº по заданной формуле.
Задача 3. На рисунке изображен график изменения температуры воздуха на протяжении суток .

Используя график определите какой температура воздуха была в 4 ч, в 10 ч, в 14 ч, в 22 ч. Оформите решение задачи в виде таблицы .

Задача 4. Вычислите значение y по формуле y=2x-13, если x=5; x=-3; x=9; x=0; x=21. Данные занесите в таблицу. В пустых клетках таблицы придумайте свое значение x и найдите соответствующее ему значение y по заданной формуле .

Учащиеся по группам проверяют домашнее задание, сверяют решения и если есть ошибки исправляют их, если возникают споры, то консультант обращается к учителю. После проверки консультанты сообщают о результатах: «Все проверено ошибок нет или все найденные ошибки исправлены».

3. Актуализация опорных знаний. Открытие нового знания. Формулирование темы урока.

Цель: опираясь на опыт, накопленный учениками в 5-6 классах, выделяя существенные признаки нового понятия, подвести их открытию нового знания и формулировке темы урока.

Деятельность учителя и ученика.

Обсуждение домашних задач. Вопросы учителя: «О каких изменениях говорится в первой задаче? Назовите переменные величины. Какую из них величину мы вычисляем по формуле?» Поставленные вопросы не вызывают затруднений у учащихся, и они сообщают о том, что в первой задаче говорится об изменения объема воды в цистерне, переменные величины время и оставшийся объем жидкости, который вычисляется по формуле.

Ученики называют свои значения, а учитель уточняет: «Формула которую вы составили для решения задачи является правилом по которому мы можем найти любое значение переменной V(t), зная значение независимой переменной t. Как вы думаете, почему я назвала t независимой переменной?» Ученики догадываются, что она независимая, потому что может принимать любое значение, которое мы ей присваиваем.
Учитель просит вспомнить слова антонимы и назвать антоним к слову «независимая» — так появляется термин «зависимая», учитель сообщает, что переменная V(t) называется зависимой переменной и подчеркивает, что в этой задаче формула задает правило, с помощью которого по значению независимой переменной можно однозначно (или единственным образом) найти значение зависимой переменной. Далее учитель просит выделить в услышанном тексте главное, существенное и записать ключевые слова на листах с домашним заданием (на которых заранее выделено место для примечаний и уточнений). Учащиеся выписывают без затруднений новые понятия: правило (формула), независимая переменная, зависимая переменная, однако не всем понятен незнакомый для них термин однозначность, поэтому учитель должен обратить внимание учеников на то, что по формуле и независимой переменной мы получаем единственное значение зависимой переменной, и в этом заключается смысл однозначности.

Обсуждая вторую задачу учитель просит назвать независимую переменную, правило (формулу) по которому можно найти соответствующее ей единственное значение зависимой переменной, зависимую переменную. Просит учеников самостоятельно сформулировать вывод.
В третьей задаче на графике показана зависимость температуры воздуха Т (температуры) от величиныt (времени). При ее обсуждении следует уделить внимание правилу (оно не задано формулой, поэтому для учеников неявно) по которому был построен график. Исходя из личного опыта (в курсе математики 6 класса им приходилось уже строить графики, и они знают порядок действий), ученики находят правило (перечисляют порядок своих действий): измеряем температуру в определенный момент времени, отмечаем соответствующую точку на графике.
Ученики замечают, что в четвертой задаче формула никак не связана с реальной ситуацией, учитывая, что уже отработан аппарат построения математической модели, учитель задает вопрос: «А можем ли мы придумать задачу, которая будет решаться по заданной формуле?», ученики соглашаются. На данном этапе урока нет необходимости требовать придумать задачу, это задание нужно отнести к творческой части домашнего задания.

В процессе обсуждения каждой задачи ключевые термины: правило, независимая переменная, зависимая переменная, однозначность проговариваются в устной форме и записываются на листах с домашним заданием в графе: «Пояснения и уточнения».

Учитель обращается к ученикам: «Задачи, которые мы рассмотрели, описывают различные математические модели, но что-то общее в них все-таки есть, подумайте и назовите, что?» Ученики без затруднений отвечают на поставленный вопрос.

Учитель сообщает ученикам о том, что в математике правило, с помощью которого по значению независимой переменной можно однозначно (или единственным образом) найти значение зависимой переменной – называют функцией, а соответствующую зависимость одной переменной от другой – функциональной. Далее ученики самостоятельно формулируют тему урока: «Функция. Понятие функции. Функциональная зависимость». После этого тема урока записывается на доске и в тетрадях учеников. Учитель просит учащихся самостоятельно записать суть понятия функции в тетради, несколько учеников зачитывают свои формулировки, учитель при необходимости уточняет и корректирует, а консультанты проверяют у каждого ученика в своей группе правильность формулировки сверяя с эталоном на доске.

В заключение этого этапа урока учитель сообщает ученикам, что впервые термин «функция» употребил немецкий математик Лейбниц в 1673 (от латинского functio — совершение, выполнение), а первое определение функции была дано в 1718 году швейцарским математиком И.Бернулли. Позже, в 1748 году, великий ученый, академик Петербургской академии наук Л.Эйлер уточнил это определение. Сегодня на уроке мы не будем углубляться в историю возникновения понятия функции, но эта информация может стать темой для вашей исследовательской работы.

4. Введение новой математической символики. Первичное применение нового знания.

Цель: научить учащихся среди исследуемых зависимостей выделять функциональные, с проговариванием вслух их существенных характеристик. Грамотно использовать математическую символику, связанную с обозначением и описанием основных свойств функций.

Деятельность учителя и ученика.

Ученикам раздаются опорные карточки , которые они вклеивают в тетрадь.

Учитель предлагает учащимся самостоятельно изучить новую математическую символику, обсуждая увиденное в группах. Для того чтобы направить деятельность учеников, учитель предлагает им ответить на вопросы: «Что я вижу? Как обозначена независимая переменная? Как обозначена зависимая переменная? и т.д.» Ученики работают в группах обсуждают новую символику, замечают, что они уже сталкивались с обозначением функции, когда решали первую домашнюю задачу. Если возникают вопросы, консультанты их задают учителю. Учитель обращает внимание учеников, что в скобках записывается независимая переменная, а в некоторых случаях и зависимую переменную и правило по которому она находится называют «функцией».

Комментированное выполнение заданий: в тетрадях ученики записывают решение первой и второй домашней задачи с использованием новой символики. Взаимопроверка по эталону на доске , работа в парах.

Анализируется условие первой домашней задачи, ученики приходят к выводу, что время не может быть больше 37 часов, так как через 37 часов из цистерны выльется вся вода. Учитель сообщает, что все значения, которые принимает аргумент (независимая переменная), образует область определения функции.

Устная работа. Обсуждая вторую задачу, учащиеся оказываются в затруднении, чтобы определить допустимые значения независимой переменной нужно знать какой может быть максимальная температура воздуха и минимальная. Обсуждение этого вопроса можно отложить до следующего урока и это будет способствовать самостоятельной поисковой деятельности учащихся. В 3 задаче независимая переменная может принимать значения всех неотрицательных чисел, не превосходящие 24, так как в сутках 24 часа. В 4 задаче независимая переменная может принимать любые значения.

Учитель сообщает ученикам, что все значения которые принимает зависимая переменная, образует область значений функции. Ученики анализируют домашние задачи и определяют область значений функции.

5. Проблемная ситуация. Мотивация к дальнейшему изучению нового знания.

Цель: Повышение мотивации обучения, научить учащихся выдвигать гипотезы, подтверждать и опровергать их. Воспитывать личность гражданина, через осознание значимости предъявленного материала.

Деятельность учителя и ученика.

Учитель сообщает ученикам о том, что мы рассмотрели различные математические модели, ввели понятие функции, характеризующей процессы в которых одна переменная величина меняет свое значение единственным образом в соответствии со значением другой переменной величины. Достаточно ли, этих примеров, чтобы сделать вывод о том, что все процессы, связанные с переменными величинами – функции? Можем ли мы это проверить, опровергнуть или подтвердить?

Мнения учащихся различны, некоторые считают, что «да», некоторые считают, что «нет», кто-то считает, что невозможно. Учитель предлагает сформулировать предположение. Самостоятельно или с помощью учителя выдвигается гипотеза: «Все процессы, которые характеризуются переменными величинами – функции». Далее идет поиск решений, которые или опровергнут, или подтвердят гипотезу.
Вопрос учителя: «Что будем проверять?» Ученики четко выделяют существенные признаки функциональных зависимостей. Учитель выписывает на доске ключевые характеристики: правило, независимая переменная, зависимая переменная, однозначность.

Работа в группах. Каждой группе предлагается решить две задачи и сделать вывод. Задания оформлены на листах , на группу выдается один лист.

Поясняет решение представитель группы, которая первой справилась с заданием. Ученики видят, что во второй задаче нарушена однозначность, поэтому описанное в них правило не является функцией, все приходят к выводу, что их предположение неверно.

Мотивация на дальнейшее изучение нового понятия.

Учитель сообщает ученикам: «Давайте рассмотрим простую житейскую ситуацию: каждый день вы идете в школу одним и тем же маршрутом, и понимаете, что опаздываете. Что вы будете делать и почему?». Ученики отвечают – ускорим шаг, побежим, проедем на транспорте, потому что быстрее двигаешься, меньше времени тратишь на дорогу. Некоторые из них замечают, что время зависит от скорости. Развивая далее диалог ученики делают вывод о том, что в этой ситуации мы тоже имеем дело с функцией и легко называют независимую переменную скорости и зависимую от скорости переменную времени.

Обобщение учителя: «В этом простом примере есть незаметный, но очень важный факт: зная закон зависимости величин (функцию), вы знаете, что нужно делать сейчас, чтобы получить нужный результат потом. При запуске ракеты, мы должны точно знать куда она полетит; мы должны уметь рассчитать любые экологические риски, да и в любых других применениях, люди просто обязаны просчитывать результат. Причём, безошибочно! И это одна из тем для исследований, которые вы можете провести на различных примерах из окружающей нас действительности.

6. Подведение итогов. Рефлексия. Домашнее задание.

Цель: диагностика личностных, предметных и метапредметных результатов деятельности, учащихся на уроке, определение учениками границ своего знания и незнания, составление плана по дальнейшему изучению функции, создание ситуации успеха, мотивирующей ученика к включению в дальнейшую познавательную деятельность.

Деятельность учителя и ученика.

Учитель обращает внимание учеников на вопросы, которые были обозначены на доске в начале урока. Ученикам раздаются оценочные листы

Учитель предлагает ученикам заполнить таблицу. Среди вопросов, которые сформулировал учитель, специально обозначены вопросы, которые не рассматривались на этом уроке, но будут изучаться далее, это поможет ученикам составить план дальнейшего изучения функций. Когда таблица заполнена, ученики составляют план по дальнейшему изучению функций. Выясняется, что им необходимо изучить способы задания функции, определить линейную функцию и узнать какие процессы в реальном мире описываются линейной функцией.

Домашнее задание.

• Прочитать § 20 и устно ответить на вопросы на стр. 138. Выполнить № 759, 770.

1) Придумать задачу к формуле обозначенной в задаче 4 предыдущего домашнего задания.

2) Выбрать одну из предложенных тем исследовательской деятельности: История возникновения понятия функции. Леонард Эйлер и его вклад в развитие теории функций. Научные интересы и гениальные открытия Н. И. Лобачевского.

Источник