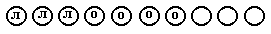Понимание способов решение задачи

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Что такое задача и способы решения.

Решение задач- это работа несколько необычная, а именно умственная работа. А чтобы научиться какой – либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется работа.

Значит, для того, чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких основных частей они состоят, каковы инструменты, с помощью которых производится решение задач.

Итак, что же такое задача?

Если приглядеться к любой задаче, то увидим, что она представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче. Поэтому, приступая к решению какой- либо задачи, надо ее внимательно изучить, установить, в чем состоят ее требования, каковы условия, исходя из которых, надо решать задачу. Все это называется анализом задачи. Вот и начнем учиться производить анализ задачи.

Структура процесса решения задач

Если под процессом решения задач понимать процесс, начинающийся с момента получения задачи до момента полного завершения ее решения, то, очевидно, что этот процесс состоит не только из изложения уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.

Из каких же этапов состоит процесс решения задачи?

Очевидно, получив задачу, первое, что нужно сделать, это разобраться в том, что эта за задача, каковы ее условия, в чем состоят ее требования. Этот анализ и составляет первый этап процесса решения задачи.

В ряде случаев этот анализ надо как – то оформить, записать. Для этого используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения.

Анализ задачи и построение ее схематической записи необходимы главным образом для того, чтобы найти способ решения данной задачи. Поиск этого способа составляет третий этап процесса решения.

Когда способ решения задачи найден, его нужно осуществить ,- это будет уже четвертый этап процесса решения – этап осуществления ( изложения ) решения.

После того, как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.

При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установит, при каких условиях задача имеет решение и при том сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д. Все это составляет шестой этап процесса решения.

Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи,- это и будет седьмой этап процесса решения.

Наконец, в учебных и познавательных целях, полезно, также произвести анализ выполненного решения, в частности, установить, нет ли другого, более рационального способа решения и т.д. Все это составляет последний, конечно же, необязательный , восьмой этап решения.

Итак, весь процесс решения задачи можно разделить на восемь этапов:

— схематическая запись задачи;

— поиск способа решения;

— формулирование ответа задачи;

— анализ решения задачи.

Приведенная схема дает лишь общее представление о процессе решения задач как о сложном и многоплановом процессе. Например:

Задача 1 . Лодка прошла по течению реки расстояние между двумя пристанями за 6 часов, а обратный путь она совершила за 8 часов. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки?

Анализ задачи . В задаче речь идет о двух объектах: лодка и плот. Лодка имеет какую – то собственную скорость, а река, по которой плывет лодка, и плот, имеет определенную скорость течения. Именно поэтому, лодка совершает путь между пристанями по течению реки за меньшее время (6ч), чем против течения (8ч). Но эти скорости (собственная скорость лодки и скорость течения реки) в задаче не даны (они не известны), также, как неизвестно расстояние между пристанями. Однако, требуется найти не эти неизвестные скорости и расстояние, а время, за которое плот проплывет неизвестное расстояние между пристанями.

Схематическая запись задачи . (рис.1.)

Поиск способа решения задачи . Нужно найти время, за которое плот проплывет расстояние между пристанями А и В. Для того, чтобы найти это время, надои знать расстояние АВ и скорость течения реки. Оба они неизвестны, поэтому обозначим расстояние АВ буквой s (км) , а скорость течения реки примем равной a км/ч. Чтобы связать эти неизвестные с данными задачи (время движения лодки по и против течения реки), нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что она равна v км/ч. Отсюда, естественно, возникает план решения, заключающийся в том, чтобы составить систему уравнений относительно введенных неизвестных.

Осуществление решения задачи . Итак, пусть расстояние АВ равно s км, скорость течения реки а км/ч, собственная скорость лодки v км/ч, а искомое время движения плота на пути в s км равно х ч. Тогда, скорость лодки по течению реки равна км/ч. За 6 ч лодка, идя с этой же скоростью, прошла путь АВ в s км. Следовательно, (1)

Против течения эта лодка идет со скоростью км/ч и путь АВ она проходит за 8 часов, поэтому (2) Наконец, плот, плывя со скоростью а км/ч, проплыл расстояние АВ за х часов, следовательно, (3) Уравнения (1), (2) и (3) образуют систему уравнений относительно неизвестных s , a , v и x . Так как требуется найти лишь х, то остальные неизвестные постараемся исключить. Для этого из уравнений (1) и (2) найдем : ; . Вычитая из первого уравнения второе, получим: , отсюда . Подставим найденное выражение для а в уравнение (3): . Так как, очевидно, , то можно обе части полученного уравнения разделить на s . Тогда найдем: х=48.

Проверка решения . Итак, мы нашли, что плот проплывает расстояние за 48 часов. Следовательно, его скорость, равная скорости течения реки, равна км/ч, а против течения км/ч. Для того, чтобы убедиться в правильности решения, достаточно проверить, будут ли равны собственные скорости лодки, найденные двумя способами:

1) от скорости лодки по течению отнять скорость течения реки, т.е. ; 2) к скорости лодки против течения реки, прибавить скорость течения реки , т.е. . Произведя вычисления, получаем верное равенство : .

Значит, задача решена правильно.

Исследование задачи . В данном случае этот этап решения не нужен.

Ответ : плот проплывет расстояние между пристанями за 48 часов.

Анализ решения . Мы свели решение этой задачи к решению системы трех уравнений с четырьмя неизвестными. Однако, найти надо было нам лишь одно из этих неизвестных. Поэтому, естественно, возникает мысль, что проведенное решение не самое удачное, хотя и достаточно простое.

Можно предложить другое решение .

Зная, что лодка проплыла расстояние АВ по течению реки за 6 ч., а против – за 8 ч., найдем, что в один час лодка, идя по течению, проходит часть этого расстояния, а против течения . Тогда разность между ними есть удвоенная часть расстояния АВ, проплываемая плотом за 1 час. Значит, плот за 1 час проплывает часть расстояния АВ , следовательно, все расстояние АВ он проплывет за 48 часов.

Как видим, при таком решении нам не понадобилось составлять систему уравнений. Однако, несомненно, это решение сложнее приведенного выше, хотя бы потому, что не всякий догадается найти разность скоростей лодки по течению и против течения реки. Часто также эту разность принимают не за удвоенную часть расстояния АВ, проплываемую плотом за 1 час, а скорость плота, что, конечно, приводит к ошибочному ответу.

Следует еще обратить внимание в приведенном решении еще на одно обстоятельство. В этом решении была получена система трех уравнений с четырьмя неизвестными. И хотя число неизвестных больше числа уравнений, из этой системы удалось найти числовое значение одного из неизвестных. Значит, не всегда такая система полностью неопределенная , в том смысле, то из неё можно найти лишь выражение одних неизвестных через другие. Как видим, в некоторых случаях из такой системы удается найти значения некоторых неизвестных (конечно, не всех).

Задача 2 . Вычислить без таблиц значение выражения

Решение. Для того, чтобы вычислить это выражение, очевидно, надо его так его преобразовать, чтобы в нем остались лишь тригонометрические функции известных углов (например, , и ) и определенные числа. Для этого надо воспользоваться известными формулами преобразования суммы и разности двух функций одного и того же аргумента. Поэтому, обозначив значение этого выражения буквой М, сгруппируем в нем попарно функции одного и того же аргумента:

М= .

Заменим котангенсы через тангенсы:

М=

Используем формулу и заменим в знаменателях тангенсы через синусы и косинусы соответствующих углов, получим после преобразований:

М = .

Теперь воспользуемся формулой синуса двойного угла:

М = .

Первую и третью дроби сгруппируем, а во второй заменим его значением:

М = .

Разность синусов преобразуем в произведение:

М = .

Зная, что , получаем окончательно:

Как видим, в этом решении трудно выделить отдельно этапы, ибо анализ, поиск решения и проверка решения производились по ходу осуществления решения. Этапы же схематической записи задачи и исследования задачи здесь вовсе оказались ненужными. Что касается анализа решения, то он также вряд ли нужен, хотя некоторое рассмотрение решения с целью закрепления в памяти использованных приемов было бы полезно.

Таким образом, структура процесса решения задачи зависит в первую очередь от характера задачи и, конечно, от того, какими знаниями знаниями и умениями обладает решающий задачу.

Приведенная выше схема решения задач является лишь примерной. При фактическом решении указанные там этапы обычно не отделены друг от друга, а переплетаются между собой. Так, в процессе анализа задачи обычно производится и поиск решения. При этом полный план решения устанавливается не до осуществления решения, а в его процессе. Тогда поиск решения ограничивается лишь нахождением идеи решения. Порядок этапов также иногда может меняться.

Стандартные задачи и их решение

Правила, пользуясь которыми можно найти последовательность шагов для решения любой задачи некоторого вида, в математике излагаются в различных формах. Приведу некоторые примеры таких правил.

Словесное правило . Примером такого правила может служить правило нахождения степени произведения: степень произведения равна произведению степеней сомножителей. Это правило позволяет составить такую программу- последовательность шагов для решения любой задачи нахождения степени произведения:

установить все сомножители произведения;

Найти данную степень каждого из этих сомножителей;

результаты второго шага перемножить

В соответствии с этой программой решение задачи : Найти будет таким:

устанавливаем, что заданное произведение состоит из трех сомножителей: 3, и ;

находим четвертую степень каждого из этих сомножителей: ; ; ;

находим произведение результатов предыдущего шага: .

Ответ: .

Заметим, что при выполнении второго шага мы, кроме рассматриваемого правила, использовали также правило возведения степени в степень.

Правило – формула . Примером такого правила служит формула корней квадратного уравнения. Корни уравнения , если и , где

, можно вычислить по формуле:

В этом правиле прямо не указана последовательность шагов для решения какого- либо квадратного уравнения. Однако легко указать эту последовательность на основе указанного правила- формулы:

проверяем условие: ;

находим: ;

проверяем условие: ;

если эти условия выполнены, то вычислим корни по формуле: .

Правило – тождество . Примером такого правила может служить тождество квадрата двучлена .

Словесная формулировка этого тождества такова: Квадрат двучлена равен сумме трех выражений: квадрата первого члена, удвоенного произведения первого члена на второй и квадрата второго члена.

В соответствии с этим тождеством можно составить такую программу- последовательность шагов для решения задачи нахождения квадрата двучлена:

найти первый член двучлена

найти второй член двучлена

возвести первый член двучлена в квадрат

возвести второй член двучлена в квадрат

составить произведение первого и второго членов двучлена

результаты 5-го шага удвоить

результаты 3, 4, и 6-го шагов сложить.

Правило- теорема . Многие теоремы могут служить правилами для решения задач соответствующего вида. Например, теорема: средняя линия трапеции параллельна ее основаниям, а длина ее равна полусумме длин оснований. Последовательность шагов для решения таких задач весьма простая:

устанавливаем длину оснований трапеции

находим их полусумму. Это и будет длина средней линии.

Правило – определение . Иногда основой для правила решений задач некоторого вида может служить определение соответствующего понятия. Примером такогоопределения является определение решения системы неравенств с одной переменной. Это определение сформулировано в таком виде: решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

На основе этого определения можно составить такую программу решения системы неравенств с одной переменной:

решить каждое из неравенств системы, получим для каждого неравенства числовой промежуток – его решение

найти пересечение (общую область) полученных числовых промежутков.

Найденное пересечение и будет решением системы неравенств.

В соответствии с этой программой решение системы неравенств:

будет состоять из последовательности следующих шагов:

решаем первое неравенство системы: , , ;

решаем второе неравенство системы: , , ;

решаем третье неравенство системы: , ,

находим пересечение числовых промежутков: , , . Получим промежуток (2; 3). Это и будет ответ задачи.

Математические задачи, для решения которых в школьном курсе математики имеются готовые правила или эти правила непосредственно следуют из каких – либо определений или теорем, определяющих программу решения этих задач в виде последовательности шагов. называются стандартными. При этом предполагается, что для выполнения отдельных шагов решения стандартных задач в курсе математики также имеются определенные правила.

Распознавание вида задачи

Когда приступаем к решению какой – либо задачи, то первое, что хочется, естественно, узнать, — это: сто за задача? Какого она вида, типа? Иными словами, нужно распознать вид данной задачи.

Если мы сумеем это сделать, установим, к какому виду задач она принадлежит, то тем самым сделаем первый, очень важный шаг в поисках плана её решения. Ведь, зная вид задачи, в большинстве случаев получаем и способ её решения, ибо в курсе математики для многих видов задач имеются общие правила их решения.

Как распознать вид задачи?

Для этого, очевидно, нужно знать основные виды математических задач и их признаки.

Первым признаком, по которому все математические задачи делятся на отдельные виды или классы, является характер требования задачи. По этому признаку все задачи делятся на три основных класса.

Первый класс . Задачи на нахождение искомого. В задачах этого класса требование состоит в том, чтобы найти, разыскать, распознать какое-то искомое. При этом искомым могут быть величина, отношения, какой- либо объект, предмет, его положение или форма и т.д.

К ним же относятся геометрические вычислительные задачи, где нужно найти длину отрезка, величину угла, площадь фигуры, объем тела и т.п.

Многочисленные задачи на решение различных уравнений, систем уравнений, неравенств и их систем также принадлежат к этому классу задач, ибо в каждой из них нужно найти значения некоторых переменных, удовлетворяющих определённых условиям.

Задачи, в которых нужно установить вид заданных выражений, чисел, форму заданной геометрической фигуры или тела, — это опять-таки задачи рассматриваемого класса.

Этот класс чрезвычайно многочисленный и разнообразный. Поэтому, естественно, для решения задач этого класса нет какого-либо общего метода. Но всё же, знаний, что данная задача принадлежит к рассматриваемому классу, сужает область поисков плана решения и служит ориентиром в этих поисках.

2 класс . Задачи на доказательство и объяснения.

В задачах этого класса требование состоит в том, чтобы убедиться в справедливости некоторого утверждения, или проверить верность или ложность этого утверждения, или, наконец, объяснить, почему имеет место то или иное явление, тот или оной факт.

3 класс . Задача на преобразование или построение.

К этому классу относятся задачи, в которых требуется преобразовать какое-либо выражение, упростить его, представить в другом виде, построить что-либо (например, геометрическую фигуру или выражение), удовлетворяющие указанным условиям.

Класс этих задач также весьма многочисленный и разнообразный .Характерной особенностью задач этого класса является то , что в каждой из них заданы какие-то объекты (элементы, выражения), из которых требуется создать, построить, сконструировать какой-то объект с заранее известными свойствами.

Конечно, в ряде случаев распознавание вида задачи представляет собой довольно сложное дело. Например.

Задача 5. Сколько центров гомотетии имеют два равных круга?

На первый взгляд кажется, что эта задача вида на нахождение искомого. К такому выводу нас наталкивает вопрос «сколько?», значит надо что- то найти. Но не следует спешить, вдумаемся в требование задачи. Нужно найти число центров гомотетии двух равных кругов. Следовательно, эти два равных круга даны и их нужно рассматривать, как гомотетичные фигуры, а требуется найти центры гомотетии, только тогда мы сможем пересчитать их и установить, сколько их. А что значит найти центры гомотетии? Это значит, по данным гомотетичным фигурам построить их центр гомотетии. Значит, данная задача фактически является задачей на построение, притом, весьма своеобразной, ибо по заданным геометическим фигурам, которые гомотетичны, необходимо построить их центр гомотетии. Подсчет же числа этих центров (после их построения) уже задачи не представляет.

Что дает нам распознавание вида задачи?

Очень многое. Ведь для большинства видов задач школьном курсе математики мы изучаем методы решения этих задач, и, следовательно, установив принадлежность данной задачи к определенному виду, тем самым получаем готовый план ее решения: применить известный метод решения подобных задач.

Источник