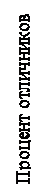Полигон частот это способ графического представления

Постройка полигона и гистограммы частот

Что такое полигон и гистограмма частот

Для наглядного представления ряда распределения используют полигон и гистограмму частот.

Полигон частот – это ломаная, соединяющая точки (x₁, n₁), (x₂, n₂). (x_k, n_k), где x_i – это варианты или наблюдаемые значения, а n_i – частота вариантов.

Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x₁, W₁), (x₂, W₂). (x_k, W_k). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

где n – это объем выборки.

Гистограмму используют в случае непрерывного признака.

Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат W_i.

Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение W_i/h.

Как построить полигон частот

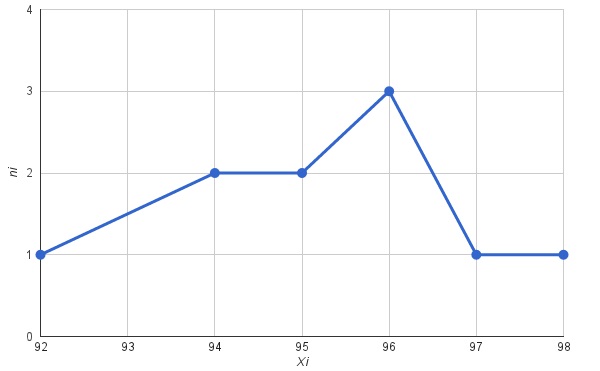
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие x_i частоты n_i. Точки с координатами (x_i, n_i), соединенные прямыми отрезками, составляют ломаную – полигон частот.

Пример

Полигон частот для выборки со следующими значениями:

x_i 92, 94, 95, 96, 97, 98.

Как построить гистограмму частот

Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты n_i/h.

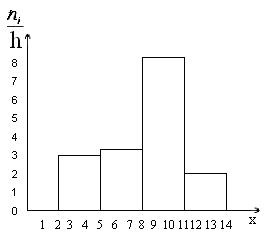
Пример гистограммы частот при частичном интервале h, равном 3.

Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.

Плотность частоты n_i/h: 3,3; 8,3.

Чему равна площадь гистограммы частот

Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:

Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.

Примеры создания полигона и гистограммы в задачах

Задача 1

Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:

Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.

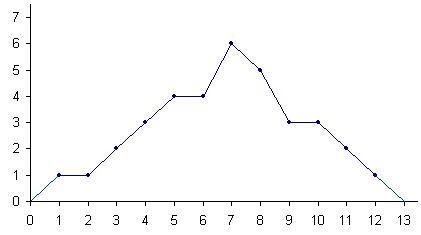
Нужно построить полигон частот по этим данным.

Решение

На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:

Задача 2

По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:

Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.

Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.

Всего в контрольной работе было 25 вопросов.

Необходимо построить гистограмму по этому ряду распределения.

Решение

Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.

Источник

Графическое представление распределения частот

Обычное представление частот не дает вполне ясной картины. Существуют три общих метода графического представления распределения оценок: гистограмма (столбиковая диаграмма), полигон распределения и сглаженная кривая.

Гистограмма – это последовательность столбцов, каждый из которых опирается на один разрядный интервал, а высота его отражает число случаев, или частоту, в этом разряде.

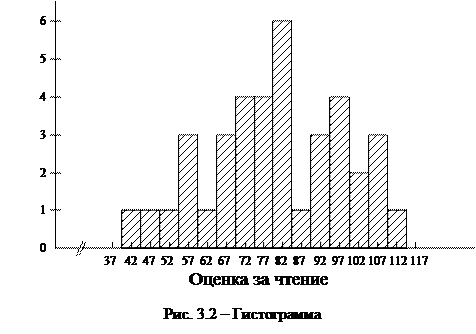На рис. 3.2 показана гистограмма распределения частот оценок за чтение (см. табл. 3.1). Поскольку наибольшая частота равна 6 в разряде 80-84, нет необходимости тянуть вертикаль или шкалу частот слева выше 6. И так как диапазон оценок распространяется от разряда 40–44 до разряда 110–114, нужно изображать горизонтальную шкалу только в этом диапазоне. Для ясности, однако, принято распространять шкалу на один разрядный интервал вправо и влево от этого диапазона. Чтобы фигура не получилась слишком приплюснутой или слишком вытянутой, обычно выбирают масштаб так, чтобы отношение высоты гистограммы к ее ширине было приблизительно 3:5. Середина столбца совмещается с серединой интервала разряда. Гистограмму принято изображать либо отдельными столбцами, либо в форме контура.

Построение полигона распределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых. Так как на разрядах справа и слева от разрядов распределения частота имеет нулевое значение, полигон заканчивается соединением точек, представляющих наивысший и наинизший разряды, с координатной осью на серединах следующих интервалов. Рис. 3.3 изображает полигон для данных гистограммы рис. 3.2.

Иногда вместо гистограммы или полигона строят сглаженную кривую. Единственная разница состоит в том, что сглаженная линия проводится по точкам настолько близко, насколько это возможно, а для других двух фигур используются линии с углами или зубцами.

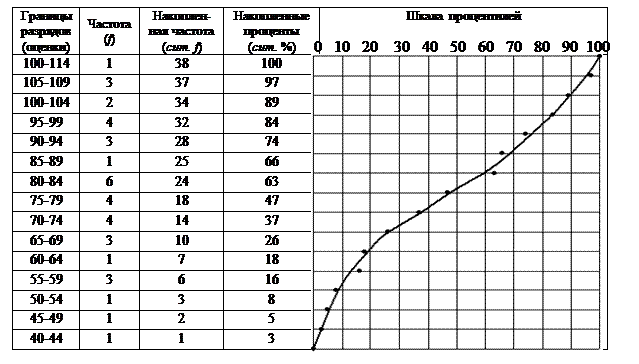
На рис. 3.4 приведена кривая процентилей для тех же данных, по которым ранее строили гистограмму и полигон. Точки, определяющие кривую процентилей, расположены на горизонталях у верхней границы каждого разряда, в позиции, которая указывает по горизонтальной шкале процент всех оценок, лежащих не выше этого разряда. Столбцы 1–3 взяты из табл. 3.1. Столбец накопленных процентов показывает, какую часть от целого составляет процент каждой из этих накопленных частот. n = 38 составляет 100 %, 37 составляет 97 % от 38, 34 составляет 89 % от 38 и т.д. Каждое значение в столбце накопленных процентов представлено как точка на верхней границе своего разрядного интервала (на горизонтали, отделяющей данный разряд от верхнего), поскольку она учитывает процент оценок в этом разряде. Эти точки определяют кривую. Как правило, особенно для малых групп, где чаще всего встречаются неравномерности, лучше пропустить некоторые точки, чтобы получить плавную и правильную кривую; но следует позаботиться о том, чтобы оставить приблизительно одинаковое количество точек по обе стороны кривой. Тогда кривая процентилей будет как можно лучше сглаживать отклонения точек.

Рис. 3.4 – Кривая процентилей

Наиболее легкой для восприятия является гистограмма. Но если нужно сравнить два или более распределения, то лучше использовать другие виды графиков, так как гистограммы накладываются друг на друга и выглядят очень запутанно. Важнейшим преимуществом кривой процентилей является возможность оценить с высокой степенью точности квартили, децили и другие аналогичные точки. Поскольку частоты для этих кривых выражены в процентах, то можно сравнивать группы неравного объема. Полигоны можно сравнивать либо для групп равного объема, либо преобразовывая частоты в относительные. Однако, уже в случае трех распределений, изображенных на одном графике, линии многократно пересекаются, а, значит, трудно проанализировать результаты.

Запутанные графики

Лучшая защита от ошибок – изучение нескольких примеров неудачных графиков.

Рис. 3.5 показывает процент отличников в выпускном классе школы за период с 2000 г. по 2003 г. Процент отличников постепенно растет от 7 в 2000 г. до 11 в 2003 г. Однако, из-за того, что вертикальная шкала графика начинается не с 0 %, как это следовало бы сделать, создается впечатление, что процент отличников в 2003 г. в 3,5 раза выше, чем в 2000 г. Действительные отношения процентов отличников по годам выясняются лишь тогда, когда шкала начинается от 0 и идет до 11 %.

На рис. 3.6 изображен процент отличников в 2000 и 2003 гг. Диаметр каждого круга соответствует проценту отличников. Однако глаз любого человека охватывает площади кругов. И хотя диаметр круга Б равен 11/7 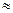1,57 диаметра круга А, площадь круга Б в (11/7) 2 2,5 раза больше площади круга А.

Еще одной серьезной ошибкой при построении рисунков и графиков является некорректное либо неполное описание осей координат, отсутствие разметки осей.

Источник

Ряды распределения

После определения группировочного признака, количества групп и интервалов группировки данные сводки и группировки представляются в виде рядов распределения и оформляются в виде статистических таблиц.

Ряд распределния является одним из видов группировок.

Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.

В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:

• Атрибутивными — называют ряды распределения, построенные по качественными признакам.
• Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.

В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются . Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.
Во втором столбце содержится количество конкретных вариант, выраженное через частоты или частости:

Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают . Сумма всех частот равна должна быть равна численности единиц всей совокупности.

Частости ( ) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.

Графическое изображение рядов распределения

Наглядно ряды распределения представляются при помощи графических изображений.

Ряды распределения изображаются в виде:

Полигон

При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.

Полигон на рис. 1 построен по данным микропереписи населения России в 1994 г.

Домохозяйства, состоящие из:	одного человека	двух человек	трех человек	5 или более	всего
Число домохозяйств в %	19,2	26,2	22,6	20,5	100,0

Рис. 1. Распределение домохозяйств по размеру

Условие: Приводятся данные о распределении 25 работников одного из предприятий по тарифным разрядам:
4; 2; 4; 6; 5; 6; 4; 1; 3; 1; 2; 5; 2; 6; 3; 1; 2; 3; 4; 5; 4; 6; 2; 3; 4
Задача: Построить дискретный вариационный ряд и изобразить его графически в виде полигона распределения.
Решение:
В данном примере вариантами является тарифный разряд работника. Для определения частот необходимо рассчитать число работников, имеющих соответствующий тарифный разряд.

Тарифный разряд Xi	Число работников fi
1	3
2	5
3	4
4	6
5	3
6	4
Итого:	25

Полигон используется для дискретных вариационных рядов.

Для построения полигона распределения (рис 1) по оси абсцисс (X) откладываем количественные значения варьирующего признака — варианты, а по оси ординат — частоты или частости.

Если значения признака выражены в виде интервалов, то такой ряд называется интервальным.
Интервальные ряды распределения изображают графически в виде гистограммы, кумуляты или огивы.

Статистическая таблица

Условие: Приведены данные о размерах вкладов 20 физических лиц в одном банке (тыс.руб) 60; 25; 12; 10; 68; 35; 2; 17; 51; 9; 3; 130; 24; 85; 100; 152; 6; 18; 7; 42.
Задача: Построить интервальный вариационный ряд с равными интервалами.
Решение:

1. Исходная совокупность состоит из 20 единиц (N = 20).
2. По формуле Стерджесса определим необходимое количество используемых групп: n=1+3,322*lg20=5
3. Вычислим величину равного интервала: i=(152 — 2) /5 = 30 тыс.руб
4. Расчленим исходную совокупность на 5 групп с величиной интервала в 30 тыс.руб.
5. Результаты группировки представим в таблице:

Размер вкладов тыс.руб Xi	Число вкладов fi	Число вкладов в % к итогу Wi
2 — 32	11	55
32 — 62	4	20
62 — 92	2	10
92 — 122	1	5
122 — 152	2	10
Итого:	20	100

При такой записи непрерывного признака, когда одна и та же величина встречается дважды (как верхняя граница одного интервала и нижняя граница другого интервала), то эта величина относится к той группе, где эта величина выступает в роли верхней границы.

Гистограмма

Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).

На рис. 2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.

Все население	В том числе в возрасте
до 10	10-20	20-30	30-40	40-50	50-60	60-70	70 и старше	Всего
Численность населения	12,1	15,7	13,6	16,1	15,3	10,1	9,8	7,3	100,0

Рис. 2. Распределение населения России по возрастным группам

Условие: Приводится распределение 30 работников фирмы по размеру месячной заработной платы

Размер заработной платы руб. в месяц	Численность работников чел.
до 5000	4
5000 — 7000	12
7000 — 10000	8
10000 — 15000	6
Итого:	30

Задача: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты.
Решение:

1. Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
2. Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда.
   Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.
3. Построим гистограмму:

Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.

Кумулята

Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости (рис. 3).

Рис. 3. Кумулята распределения домохозяйств по размеру

4. Рассчитаем накопленные частоты:
Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.

Размер заработной платы руб в месяц Xi	Численность работников чел. fi	Накопленные частоты S
до 5000	4	4
5000 — 7000	12	16
7000 — 10000	8	24
10000 — 15000	6	30
Итого:	30	—

При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:

Огива

Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.

Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака.

Равномерному распределению признака соответствует на графике диагональ квадрата (рис. 4). При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.

Источник