Показатели вариации способ их вычисления

Показатели вариации и способы их расчета

Понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные (случайные), которые на одни единицы совокупности могут оказывать влияние, на другие нет.

Вариация, порождаемая существенными факторами, носит систематический характер, т.е. наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называется систематической. В систематической вариации проявляются взаимосвязи между явлениями, их признаками, в такой связи — один как причина (фактор), другой как следствие (результат) его действия. Точнее говоря, проявляется зависимость вариации одного признака от вариации другогоили от нескольких других.

Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.

Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации. Но систематическая вариация, если между признаками имеется довольно существенная связь, в конце концов пробивает себе дорогу через хаос случайных колебаний вариантов зависимого признака и проявляет себя.

Наличие вариации признаков, изучаемых статистикой явлений, ставит задачу определить меру вариации, ее измерение, найти соответствующие измерители — показатели, характеризующие размеры этой вариации, а также выявить сущность и методы вычисления определяющих ее факторов.

Показатели вариации и способы их расчета

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. Исчислив среднюю арифметическую по данным вариационного ряда, мы не знаем о том, как отдельные значения изучаемого признака группируются вокруг средней. Для вариационного ряда важно изучать степень сплоченности всех отдельных значений признака вокруг его среднего значения, степень разбросанности этих значений, степень их колеблемости. Для этого в теории статистики используются показатели вариации.

Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. К относительным показателям вариации относятся: коэффициенты вариации, осцилляции, относительное линейное отклонение и др. Относительные показатели вычисляются как отношение абсолютных показателей вариации к средней величине.

1.Размах вариации (R)представляет собой разность между максимальным (x_max) и минимальным (x_min) значением признака исследуемой совокупности:

.

Размах вариации (амплитуда колебаний) дает лишь самое общее представление о размерах вариации, характеризует предел изменения значений признака в исследуемой совокупности. Этот показатель вариации обладает существенным недостатком: он характеризует только отклонения и не дает представление о распределении отклонений по все совокупности. Его величина определяется двумя крайними значениями признака, в то время как колеблемость последнего в целом складывается из всех его значений. Для анализа вариации необходим показатель, который бы отражал все колебания варьирующего признака и давал обобщенную его характеристику.

2. Среднее линейное отклонение ( 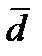)– это среднее из абсолютных отклонений значений признака от средней арифметической:

, .

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю.

Таково в среднем линейное отклонение вариантов признака от их средней величины. Если среднее линейное отклонение по сравнению со средней величиной признака небольшое, это свидетельствует о том, что данная совокупность в отношении нашего признака однородна, а средняя – типична. Таким образом, среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности.

3. Дисперсия – это среднее из квадратов отклонений индивидуальных значений признака от средней величины:

, .

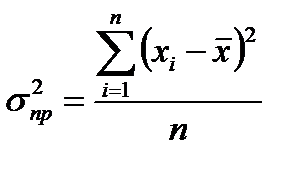
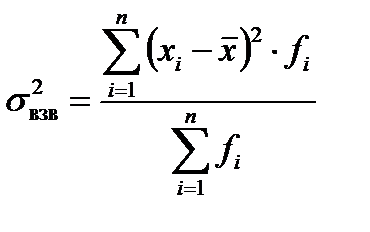
Математические свойства дисперсии

1) Дисперсия постоянной величины равна нулю:

.

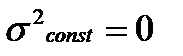
2) Дисперсия не изменится, если все значения признака увеличить или уменьшить на некоторую постоянную величину А.

.

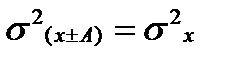
3) Если все значения варьирующего признака разделить (умножить) на одну и ту же величину h, то дисперсия уменьшится (увеличится) в h 2 раз.

, .

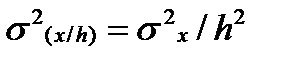
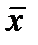
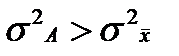
4)Средний квадрат отклонений индивидуальных значений признака от любой величины А, отличающейся от средней арифметической (A ≠ ), всегда больше среднего квадрата отклонений, исчисленного от средней арифметической:

или .

Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней от этой условно взятой величины А, т.е. на .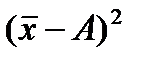

Другими словами, дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин.

или .

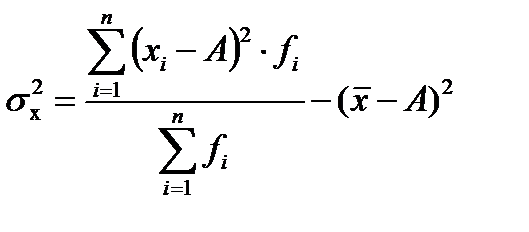
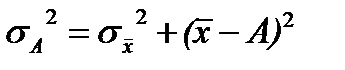
В случае когда А приравнивается нулю и, следовательно, отклонения не вычисляются, формула принимает следующий вид:

, или .

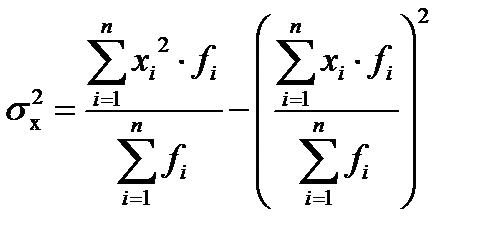
4.Среднее квадратическое отклонение находится как корень из дисперсии. Показывает (как и среднее линейное отклонение) на сколько в среднем индивидуальные значения признака отклоняются от средней арифметической:

, .

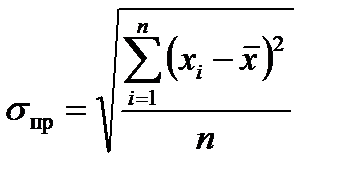
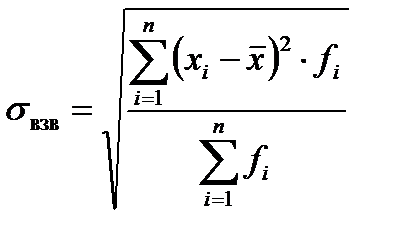
5.Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:

.

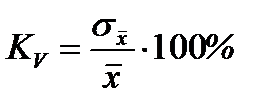
Считается, что если коэффициент вариации превышает 33%, то совокупность нельзя признать качественно однородной. Если K_v ≤ 33%, то можно утверждать, что совокупность более или менее однородна, а следовательно, средняя, рассчитанная по такой совокупности, типична. Необходимость исчисления коэффициента вариации вызвана тем, что показатели вариации в абсолютных величинах, как правило, непосредственно несравнимы.

Пример. Рассчитать показатели вариации по имеющимся данным (табл. 8.1).

Таблица 8.1 – Распределение предприятий по объему продаж

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе
1-5
5-9
9-13
13-17
17-21
ИТОГО

Алгоритм расчета показателей вариации следующий:

1) определим размах вариации:

R = 21 – 1 = 20 млн. руб.

2) найдем середину интервалов по исходным данным (x_i) и запишем в табл. 8.2;

3) определим среднее значение по формуле средней арифметической взвешенной, для этого введем графу (x_i f_i):

млн. руб.

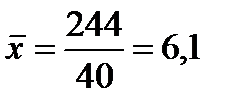
4) для расчета среднего линейного отклонения введем графы и :

млн. руб.

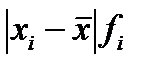
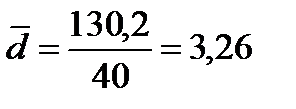
Таково в среднем отклонение вариантов признака от их средней величины.

5) для расчета дисперсии введем графы и :

.

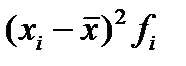
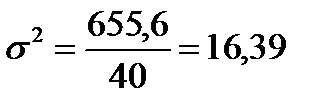
6) рассчитаем дисперсию упрощенным способом, для этого введем графу ( ):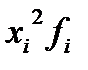

.

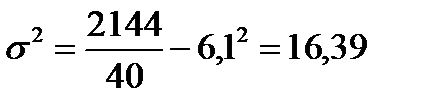
7) извлечем из дисперсии корень и получим среднее квадратическое отклонение:

млн. руб.

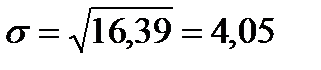
8) определим коэффициент вариации:

или 66%.

K_v > 33%, следовательно, изучаемая совокупность качественно неоднородна и рассчитанное среднее значение нетипично.

Таблица 8.2 – Расчет показателей вариации

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе, fi	Середина интервала, xi	xi fi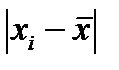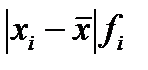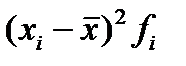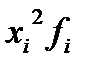
1-5	3,1	65,1	9,61	201,81
5-9	0,9	9,9	0,81	8,91
9-13	4,9	24,5	24,01	120,05
13-17	8,9	17,8	79,21	158,42
17-21	12,9	12,9	166,41	166,41
ИТОГО	—	—	130,2	—	655,6

Дата добавления: 2015-12-26 ; просмотров: 11312 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Показатели вариации: понятие, виды, формулы для вычислений. Примеры решения задач

Часто в статистике при анализе какого-либо явления или процесса необходимо учитывать не только информацию о средних уровнях исследуемых показателей, но и разброс или вариацию значений отдельных единиц, которая является важной характеристикой изучаемой совокупности.

В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды времени и в разных местах.

Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации представляет собой разность максимального и минимального значений признака: R = Xmax – Xmin. Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.

Дисперсия лишена этого недостатка. Она рассчитывается как средний квадрат отклонений значений признака от их средней величины:

Упрощенный способ расчета дисперсии осуществляется с помощью следующих формул (простой и взвешенной):

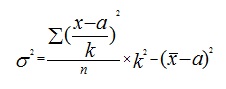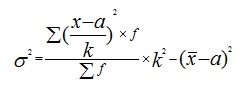Примеры применения данных формул представлены в задачах 1 и 2.

Широко распространенным на практике показателем является среднее квадратическое отклонение:

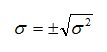Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак.

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении — относительно среднего уровня, что во многих случаях является предпочтительнее.

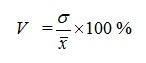— формула для расчета коэффициента вариации.

Примеры решения задач по теме «Показатели вариации в статистике»

Задача 1. При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:

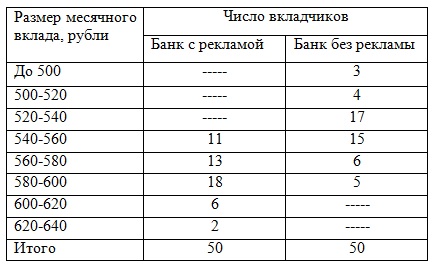Определить:
1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада;
2) средний размер вклада за месяц для двух банков вместе;
3) Дисперсию вклада для 2-х банков, зависящую от рекламы;
4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы;
5) Общую дисперсию используя правило сложения;
6) Коэффициент детерминации;
7) Корреляционное отношение.

Решение

1) Составим расчетную таблицу для банка с рекламой. Для определения среднего размера вклада за месяц найдем середины интервалов. При этом величина открытого интервала (первого) условно приравнивается к величине интервала, примыкающего к нему (второго).

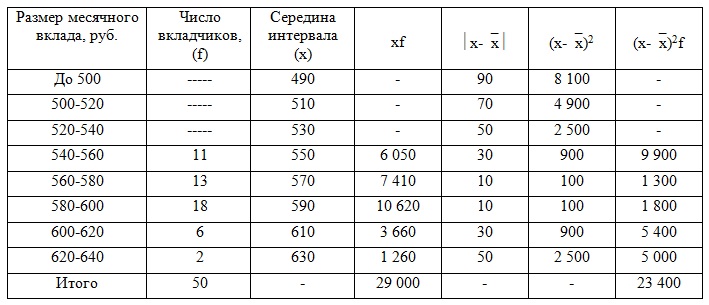Средний размер вклада найдем по формуле средней арифметической взвешенной:

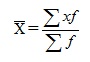= 29 000/50 = 580 руб.

Дисперсию вклада найдем по формуле:

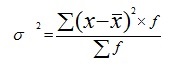Аналогичные действия произведем для банка без рекламы:

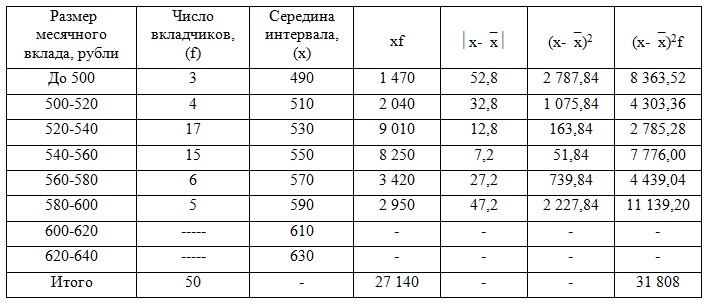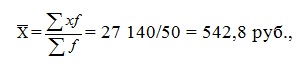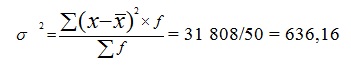2) Найдем средний размер вклада для двух банков вместе. Хср =(580×50+542,8×50)/100 = 561,4 руб.

3) Дисперсию вклада, для двух банков, зависящую от рекламы найдем по формуле: σ 2 =pq (формула дисперсии альтернативного признака). Здесь р=0,5 – доля факторов, зависящих от рекламы; q=1-0,5, тогда σ 2 =0,5*0,5=0,25.

4) Поскольку доля остальных факторов равна 0,5, то дисперсия вклада для двух банков, зависящая от всех факторов кроме рекламы тоже 0,25.

5) Определим общую дисперсию, используя правило сложения.

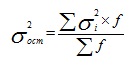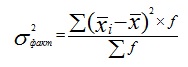= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96

σ 2 = σ 2 факт + σ 2 ост = 552,08+345,96 = 898,04

6) Коэффициент детерминации η 2 = σ 2 факт / σ 2 = 345,96/898,04 = 0,39 = 39% — размер вклада на 39% зависит от рекламы.

7) Эмпирическое корреляционное отношение η = √η 2 = √0,39 = 0,62 – связь достаточно тесная.

Задача 2. Имеется группировка предприятий по величине товарной продукции:

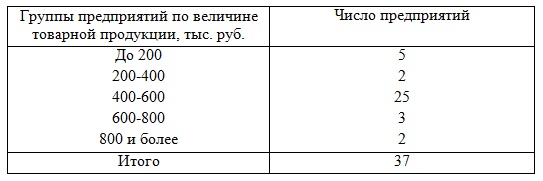Определить: 1) дисперсию величины товарной продукции; 2) среднее квадратическое отклонение; 3) коэффициент вариации.

Решение

1) По условию представлен интервальный ряд распределения. Его необходимо выразить дискретно, то есть найти середину интервала (х’). В группах закрытых интервалов середину найдем по простой средней арифметической. В группах с верхней границей — как разность между этой верхней границей и половиной размера следующего за ним интервала (200-(400-200):2=100).

В группах с нижней границей – суммой этой нижней границы и половины размера предыдущего интервала (800+(800-600):2=900).

Расчет средней величины товарной продукции делаем по формуле:

Хср = k×((Σ((х’-a):k)×f):Σf)+a. Здесь а=500 — размер варианта при наибольшей частоте, k=600-400=200 — размер интервала при наибольшей частоте. Результат поместим в таблицу:

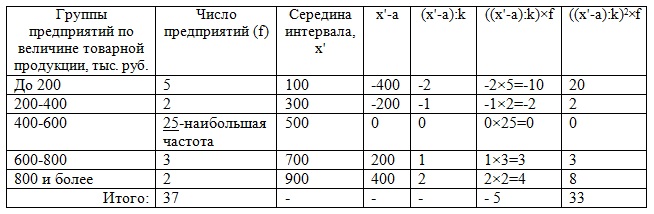Итак, средняя величина товарной продукции за изучаемый период в целом равна Хср = (-5:37)×200+500=472,97 тыс. руб.

2) Дисперсию найдем по следующей формуле:

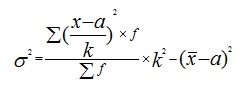σ 2 = (33/37)*2002-(472,97-500)2 = 35 675,67-730,62 = 34 945,05

3) среднее квадратическое отклонение: σ = ±√σ 2 = ±√34 945,05 ≈ ±186,94 тыс. руб.

4) коэффициент вариации: V = (σ /Хср)*100 = (186,94 / 472,97)*100 = 39,52%

Другие статьи по данной теме:

Список использованных источников

1. Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
2. Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003;
3. Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
4. Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;

2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна

Источник