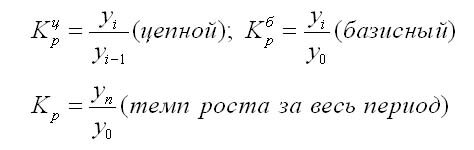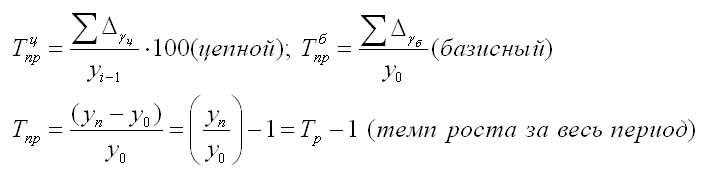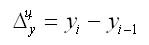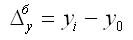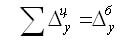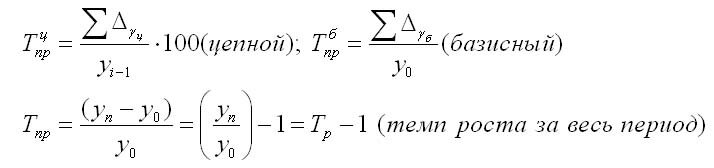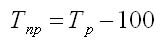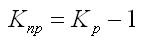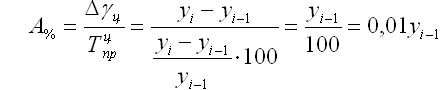Показатели динамики это способ

Ряды динамики

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

1. По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
2. По форме представления — ряды абсолютных, относительных и средних величин.
3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
4. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

• абсолютное изменение (абсолютный прирост);
• относительное изменение (темп роста или индекс динамики);
• темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого	-2,3	0,984	-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

В нашем примере про число жителей России подтверждается правильность расчета абсолютных изменений: = — 2,3 рассчитана в итоговой строке 4-го столбца, а = — 2,3 – в предпоследней строке 3-го столбца расчетной таблицы.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.

• 
• 
• 

• Разработка интернет-магазина
• Редизайн сайта эвакуации
• Редизайн сайта доставки суши

Источник

Вопрос 3. Показатели динамики. Методы расчета

Показатели динамики – это величины, характеризующие изменение уровней динамического ряда. К ним относятся: абсолютный прирост, коэффициент (темп) роста, коэффициент (темп) прироста.

В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики – это результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу, они характеризуют окончательный результат всех изменений в уровнях ряда за период от базисного до текущего уровня. Обычно за базу сравнения принимают начальный уровень динамического ряда. Цепные показатели динамики – это результат сравнения текущих уровней с предшествующими, они характеризуют интенсивность изменения от срока к сроку.

Методы расчета показателей динамики в зависимости от базы сравнения показаны в таблице:

Показатели динамики	Базисные	Цепные
Абсолютный прирост Аt	Аt=xt–x0	аt= xt–xt–1
Коэффициент роста It	It= xt/x0	it= xt/xt-1
Темп роста It×100%	It×100%	it×100%
Коэффициент прироста Кt	Кt=(xt–x0)/x0= It–1	kt=(xt–xt-1)/xt-1=it–1
Темп прироста Кt×100%	Кt×100%	kt×100%
<хt> – уровни динамического ряда; х0 – базисный уровень.

Абсолютный прирост характеризует на сколько единиц уровень текущего периода больше или меньше уровня базисного или предыдущего периода. Он измеряется в тех же единицах, что и уровни ряда.

Коэффициент роста показывает во сколько раз уровень текущего периода больше или меньше базисного или предыдущего. Этот показатель, выраженный в процентах, называют темпом роста.

Темп прироста показывает на сколько процентов текущий уровень больше или меньше базисного или предыдущего.

Определяя цепные показатели динамики, получают ряд варьирующих, отчасти независимых величин, для которых можно определить средние характеристики. Предварительно необходимо рассмотреть взаимосвязь базисных и цепных показателей динамики, используя уже принятые обозначения:

Средний абсолютный прирост определяется как среднее арифметическое из абсолютных приростов за отдельные периоды времени динамического ряда:

где n – число приростов.

Средний коэффициент роста определяется как среднее геометрическое из коэффициентов роста за отдельные периоды времени динамического ряда:

Среднегодовой темп прироста определяют исходя из среднего темпа роста:

Источник

Показатели динамики: темп роста и темп прироста

Темп роста

Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.

Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста

Коэффициент роста может быть рассчитан по формулам:

Также темп роста может определяться так:

Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.

Абсолютный прирост

Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:

1. Абсолютный прирост (цепной):

2. Абсолютный прирост (базисный):

где уi — уровень сравниваемого периода;

Уi-1 — Уровень предшествующего периода;

У0 — уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:

Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.

Темп прироста

Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:

Темп прироста можно получить из темпа роста:

Коэффициент прироста может быть получен таким образом:

Абсолютное значение 1%-го прироста

Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:

Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

Примеры расчетов показателей динамики

Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики

О показателях динамики

При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.

Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.

Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.

Источник