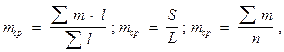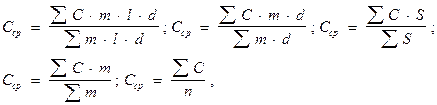Подсчет средних содержаний запасов полезных ископаемых
Химические анализы проб, определения объемных весов и замеры мощностей, производимые в разведочных выработках, являются исходным материалом для определения средней мощности, объемного веса и содержания, характерных для подсчитываемого тела. Запасы обычно подсчитывают по отдельным участкам (блокам), на которые подразделяется каждое подсчитываемое тело. Так как контуры блоков во многих случаях определяются несколькими выработками, то первоначально вычисляются средние величины по отдельным выработкам. Впоследствии среднее содержание, средний объемный вес и средняя мощность подсчитываются для всего блока на основании средних величин по выработкам, относящимся к блоку.
В этом разделе мы останавливаемся только на подсчете средних содержаний промышленных компонентов, так как он аналогичен в обычных случаях подсчету других средних показателей. Детально методика определения средних показателей освещается при разборе способов подсчета запасов.
В результате опробования горно-разведочных выработок обычно устанавливаются:
1) среднее содержание компонента по каждому забою;
2) среднее содержание по отдельным горным выработкам;
3) среднее содержание по блокам.
Во всех трех случаях подсчеты ведутся по одной из двух основных формул.
По формуле среднего арифметического:
где с1, с2, с3 и т. д. — значения содержаний исследуемого компонента по отдельным пробам забоя или выработки, например штрека или восстающего;
n — количество секционных проб в забое, выработке или в нескольких выработках.
Вторая формула отличается от первой введением некоторой величины а, которая может представлять собой: длину отдельных секций (l) бороздовой пробы по мощности рудного тела, объемный вес (d) опробуемой руды, произведение (ld), площадь участка (S-блока) или его объем (V).
При опробовании забоя секционной бороздой среднее содержание исследуемого компонента по данному забою вычисляется как среднее арифметическое по отдельным секциям, если длины отдельных секций и объемные веса руды каждой секции близки между собой. В частности, для забоя, опробованного бороздой, состоящей из трех секций равной длины (рис. 201) и с близким объемным весом руды каждой секции, среднее содержание будет равно:
Если же объемные веса руд отдельных секций колеблются резко и, во всяком случае, не являются более или менее близкими, подсчет среднего содержания по забою ведется по среднему взвешенному относительно объемных весов.
В этом случае среднее содержание будет равно:
где значения c1, c2 и c3 — те же, что и выше, a d1, d2, d3 — объемные веса руд соответствующих секции.
По второй формуле подсчитывается среднее содержание также тогда, когда длины отдельных секций борозды в забое различны.
В данном случае среднее содержание С будет равно:
где l1, l2, l3 — длины соответствующих секций борозды, а остальные обозначения — те же, что и выше.
Если при этом так же резко колеблются объемные веса руды, то подсчет ведется по среднему взвешенному относительно длин секций и объемных весов. Среднее содержание по забою в этом случае будет равно:
Подсчет по отдельным выработкам производится как методом среднего арифметического, так и методом среднего взвешенного. Среднее содержание по выработке, ориентированной вкрест простирания тела полезного ископаемого, подсчитывается способом среднего арифметического при условии, что длины проб (секций) приблизительно одинаковы и объемные веса полезного ископаемого, представляемые этими пробами, близки. В тех же условиях, но при различных длинах секций проб, подсчет ведется методом среднего взвешенного относительно длин проб, причем:
где С — среднее содержание компонента по данной выработке;
c1, c2, c3 . cn — содержания по отдельным входящим в подсчет пробам (секциям);
l1, l2, l3 . ln — длины проб (секций).
При резких или более или менее значительных колебаниях объемных весов руды по отдельным пробам подсчет необходимо вести по формуле:
где значения с и l — те же, что и выше, a d1, d2 . dn — объемные веса руд по соответствующим пробам.
В выработках, ориентированных по простиранию рудных тел, величина С подсчитывается как среднее арифметическое из содержаний по пробам, если l и d колеблются не резко. Если же эти элементы подвержены колебаниям, то С подсчитывается как среднее взвешенное, пропорциональное l и d.
Подсчет среднего содержания компонента в блоках ведется по предварительно вычисленным средним содержаниям отдельных
выработок. Например, среднее содержание для блока, ограниченного двумя штреками, может быть вычислено способом среднего арифметического при условии, что длины двух горизонтальных выработок, оконтуривающих этот блок, одинаковы, в связи с чем равны и площади их влияния (SI и SII на рис. 202).
Если выработки, оконтуривающие блок, имеют разную длину, то среднее содержание компонента в блоке подсчитывают способом среднего взвешенного пропорционально длинам выработок. Подробнее об этом сказано в главе второй.
Приведенные схемы отражают принятые в практике подсчеты средних содержаний промышленно-ценных компонентов. Однако в последнее время были признаны нецелесообразными подсчеты способом среднего взвешенного пропорционально мощности, когда пробами не устанавливается прямая или обратная взаимосвязь (корреляция) между мощностью и содержанием промышленных компонентов и когда объемный вес руды колеблется в узких пределах, как это нередко имеет место.
В этих случаях подсчет средних содержаний следует производить способом среднего арифметического даже при резких колебаниях мощности рудных тел. Это обстоятельство имеет существенное практическое значение при большом количестве выработок, по которым производится подсчет содержаний, так как подсчеты в данном случае становятся менее трудоемкими.
Возможность подсчетов средних содержаний способом среднего арифметического, вместо способа среднего взвешенного, определяется обычно опытным путем. В конкретных условиях данного месторождения оба способа подсчета сравниваются на примерах достаточного количества разнообразных блоков. Если оба они дают близкие результаты или, по крайней мере, не показывают систематического увеличения или уменьшения результатов, то разрешается применять наиболее простой способ среднего арифметического.
Подсчет содержаний по скважинам ручного ударно-вращательного и ударного механического бурения ведется способом среднего арифметического или среднего взвешенного, в зависимости от равнозначности или неравнозначности величин секций и от объемных весов проб по соответствующим секциям. Несколько иначе обстоит дело с подсчетом средних содержаний по скважинам колонкового бурения.
В зависимости от процента выхода керна пробой могут являться только керн, только шлам или тот и другой вместе. Удовлетворительные результаты подсчета по шламу или по керну и шламу вместе могут получиться лишь при уверенности в том, что собранный шлам действительно соответствует пробуренному участку, не разубожен и не обогащен.
Подсчет среднего содержания только по керну, при достаточном его выходе, производится путем уравновешивания частных содержаний по подъемам на длину проходки скважины, относящуюся к подъему. При этом должна существовать уверенность, что нет резкого избирательного обеднения или обогащения керна за счет легко выкрашивающихся хотя бы небольших прожилков и прослоев, не оставшихся в поднятом керне.
Среднее содержание по скважине определяется по формуле:
где c1, c2 и т. д. — содержание полезного компонента в пробах керна по отдельным подъемам;
l1, l2 и т. д. — длина проходки скважины, относящаяся к подъему;
d1, d2 и т. д. — объемный вес руды по отдельным подъемам.
Подсчет средних содержаний по керну и шламу вместе для соответствующей секции или интервала чаще всего производится по формуле:
где С — среднее содержание исследуемого компонента на участке длиной L, вычисленное по данным анализа керна и шлама;
c1 — содержание исследуемого компонента, полученное в результате анализа керна;
с2 — содержание исследуемого компонента, полученное в результате анализа шлама;
V — объем пробуренного участка скважины длиной L;
V1 — объем керна при длине его AT;
V2 — объем шлама, извлеченного из шламовой трубы и на желобах у устья скважины с участка длиной L;
К — длина керна, полученного с пробуренного интервала L;
L — пробуренная длина участка скважины, для которой ведется подсчет среднего содержания;
D — диаметр скважины;
D1 — диаметр керна.
Подставляя приведенные значения отношении V1/V и V2/V, выраженные через К, L, D1 и D в первое равенство, получим:
Источник
Подсчет запасов



Запасы полезного ископаемого — понятие геолого-экономическое, определяющее не только количество (объем или тоннаж), но и весь комплекс параметров, характеризующих геологическое тело с точки зрения формы, свойств, условий залегания и условий ведения горно-эксплуатационных работ.
Подсчет запасов — совокупность вычислительных операций по обработке геологических материалов при разведке месторождения.
Для подсчета запасов полезных ископаемых необходимы следующие параметры: m — средняя мощность тела полезного ископаемого в пределах площади подсчета запасов (в м); С — среднее содержание полезного ископаемого (в граммах на 1 т или на 1 м 3 , или в %); d — объемный вес руды; S — площадь тела полезного ископаемого. Таким образом, если содержание выражено в %, то запасы (Р) полезного ископаемого в недрах можно представить в следующем виде:
P = m × C × d × S : 100
Среднее значение мощности тела полезного ископаемого (в зависимости от условий) рассчитывается по одной из следующих формул:
mcp — среднее значение мощности; l — длина влияния отдельных замеров мощностей; S — площадь сечения тела полезного ископаемого; L — общая протяженность тела; m — значение отдельных замеров мощности; n — количество замеров.
Среднее значение полезного компонента (в зависимости от условий) рассчитывается по формулам:
где Ccp — среднее значение содержания компонента; C — среднее содержание полезного компонента по данным отдельных проб; S — площадь влияния данной пробы; d — объемный вес руды.
Объемный вес полезного ископаемого определяется по результатам технического опробования и рассчитывается способом среднего арифметического.
Способы подсчета запасов основаны на двух главных принципах: 1) преобразование сложных по форме тел полезных ископаемых в равновеликие им по объему, но более простые по форме геометрические тела; 2) распространение геологоразведочных данных, полученных по отдельным разведочным пересечениям, на прилегающие к ним объемы недр. Известно свыше двадцати способов подсчета запасов. В практике наиболее широко применяется четыре способа: 1) среднего арифметического; 2) геологических блоков; 3) эксплуатационных блоков; 4) разрезов (сечений).
Способ среднего арифметического заключается в определении средней мощности тела полезного ископаемого по всем выработкам, расположенным в пределах контура (mcp) и площади в пределах этого контура (S), что позволяет сразу вычислить объем (V = S × m). Способ применим при равномерном распределении выработок и для месторождений простого геологического строения (1-й группы). Часто он применяется как контрольный для расчета объема вскрышных пород на месторождениях, подготавливаемых к открытой разработке.
Способ геологических блоков. Площадь подсчета запасов разделяется на отдельные участки (блоки): по степени разведанности; по мощности; по качеству (сортности) полезного ископаемого и т.д. Подсчет производится раздельно по каждому из выделенных блоков способом среднего арифметического. В случае геометрически неправильной разведочной сети является единственным способом подсчета запасов.
Формуляр подсчета запасов способом геологических блоков
| № блока и катего-рия запасов | Пло-щадь, м 2 | Сред-няя мощ-ность, м | Объем, м 3 | Объем-ный вес, т/м 3 | Запасы полез-ного ископае-мого, т | Среднее содер-жание полезного компо-нента, % | Запасы полезного ком-понента, т |
Способ эксплуатационных блоков применяется для подсчета запасов маломощных рудных тел, разведанных системами продольных разрезов с помощью горных выработок. Тело полезного ископаемого преобразуется в ряд сомкнутых по штрекам и восстающих параллелепипедов, которые и являются эксплуатационными блоками, оконтуренными и опробованными обычно с четырех сторон. Запасы в каждом блоке рассчитываются раздельно способом среднего арифметического.
Способ разрезов (сечений) позволяет наиболее полно учесть и отразить геологические особенности строения месторождений и залежей полезных ископаемых. Его применение особенно эффективно при подсчете запасов в залежах сложной формы и большой мощности. Способ обеспечивает наиболее правдоподобное преобразование объемов залежей. Он имеет несколько вариантов: вертикальных параллельных сечений, вертикальных непараллельных сечений, горизонтальных сечений. Варианты отличаются различным положением относительно залежи и друг от друга разведочных разрезов. Методика подсчета запасов: в пределах каждого разреза определяются площадь полезного ископаемого и среднее содержание полезного компонента, затем объем полезного ископаемого, заключенный между двумя соседними разрезами или разрезом и контуром рудного тела, далее — количество руды и полезного компонента в блоке. Объем блока вычисляется в зависимости от равновеликости ограничивающих его сечений по следующим формулам:

если площади относительно равновелики, то 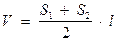
если более чем на 40% отличаются, то 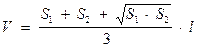
если крайний блок опирается на одно сечение, то 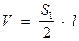
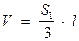
Способ широко применяется при подсчете запасов руд месторождений цветных металлов.
Формуляр подсчета запасов способом разрезов
| № блока и кате-гория запа- сов | № раз-реза | Пло-щадь полез-ного иско-пае-мого, м 2 | Расстояние между разре-зами, м | Объем блока, м 3 | Объем-ный вес, т/м 3 | Запасы полез-ного иско-пае-мого, Т | Сред-нее содер-жание полез-ного компо-нента, % | Запасы полез-ного ком-понен-та, т |
Контрольные вопросы
1. Определите понятие “подсчет запасов”.
2. Перечислите исходные материалы и параметры для подсчета запасов.
3. Какие способы подсчета запасов являются наиболее распространенными в практике геологоразведочных работ?
Источник