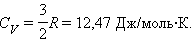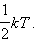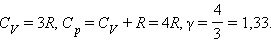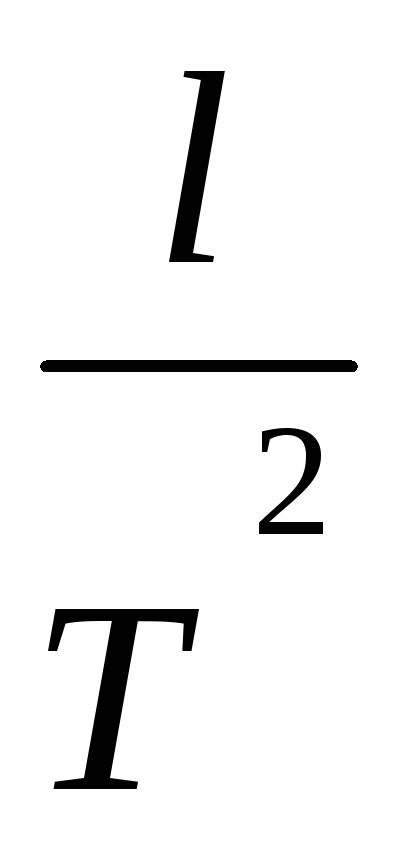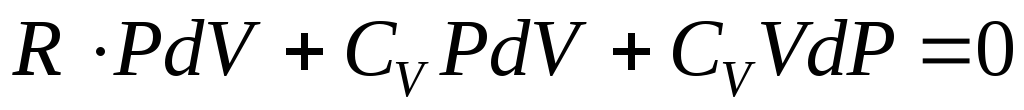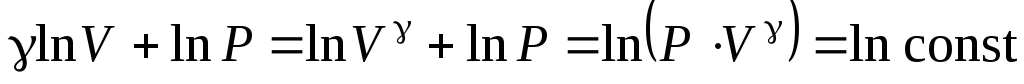Теплоемкости газов, их зависимость от характера процесса.
В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса.
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c
|
Во многих случаях удобно использовать молярную теплоемкость C:
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
|
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
|
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
 |
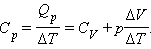Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
 или  |
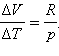Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
| Cp = CV + R. |
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости CV в процессе с постоянным объемом (рис. 3.10.1).
 |
| Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV |
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
|
 |
Термодинамические процессы, в которых теплоемкость газа остается неизменной, называются политропическими. Все изопроцессы являются политропическими. В случае изотермического процесса ΔT = 0, поэтому CT = ∞. В адиабатическом процессе ΔQ = 0, следовательно, Cад = 0.
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией 
поступательного движения молекул и абсолютной температурой T:
 |
Внутренняя энергия 1 моля идеального газа равна произведению на число Авогадро NА:
 |
При изменении температуры на ΔT внутренняя энергия изменяется на величину
|
Коэффициент пропорциональности между ΔU и ΔT равен теплоемкости CV при постоянном давлении:
|
Молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные).
В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 
Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде
|
где i – число степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i = 3)
|
Для газа, состоящего из двухатомных молекул (i = 5)
|
Для газа, состоящего из многоатомных молекул (i = 6)
|
При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:
| U = 3NАkT = 3RT. |
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
|
Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между Cp и CV из-за ничтожно малой работы при расширении или сжатии.
Источник
5.2 Описание установки и теория метода
Математический маятник представляет собой массивный шарик небольшого размера, подвешенный на длинной двойной нити, чтобы колебания происходили строго в одной плоскости (рисунок 5.5).
Рисунок 5.5
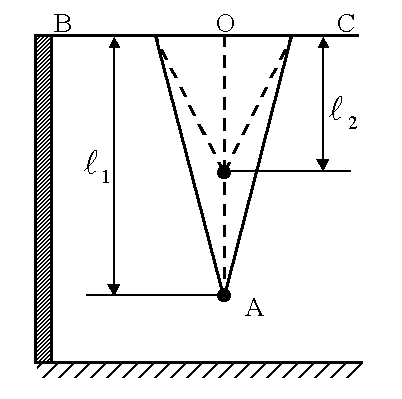
На перекладине BCподвешен на двойной нити шарик А. Длину математического маятника можно изменять, натягивая нить на барабан. Периоды колебаний математического маятникаТ1иТ2определяются при разных длинахl1 и l2 по формуле (5.12)
Т1 = 2p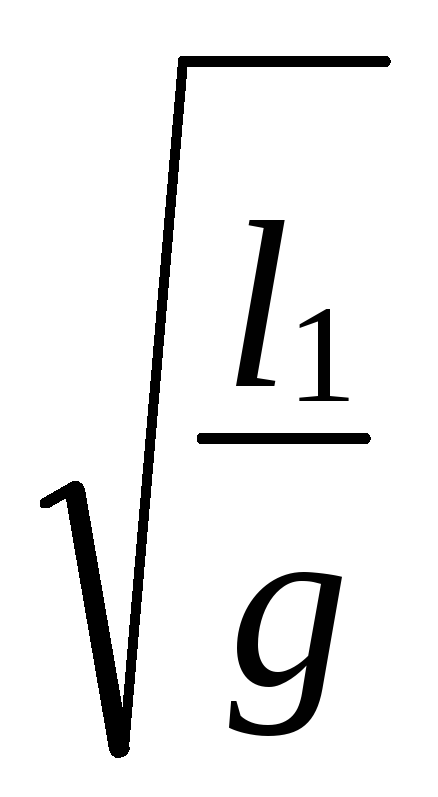
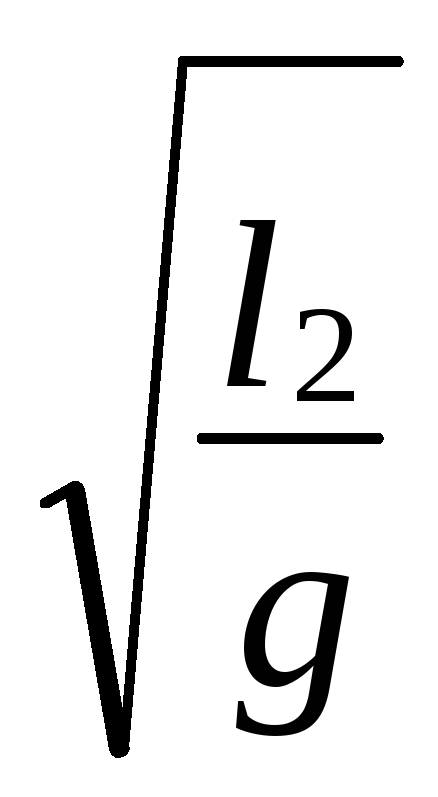
,Т2 = 2p 
(5.1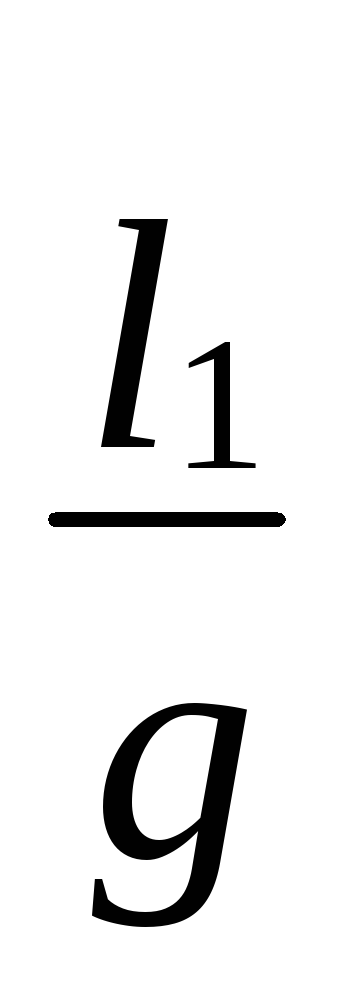3)
Т1 2 = 4p 2 
,Т2 2 = 4p 2 
и получим для ускорения свободного падения gследующее соотношение:
g = 4p 2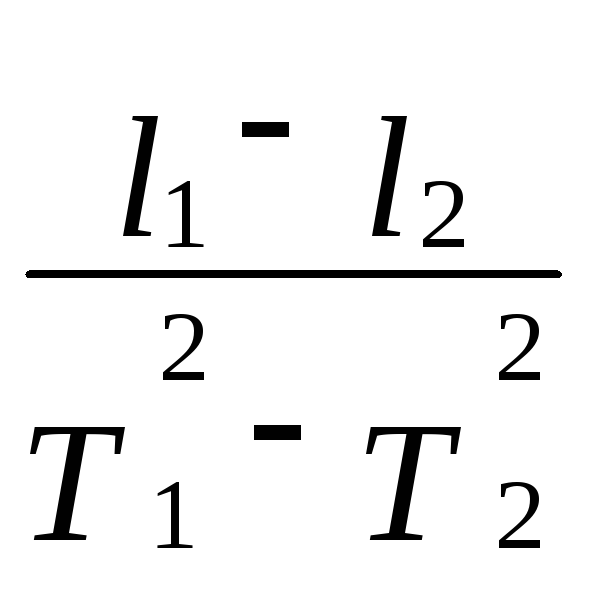 
. (5.14)
Так как в формулу (5.14) входит разность длин маятников, то можно измерить расстояние точки 0 до точки подвеса шарика (×)А (рисунок 5.5).
5.3 Порядок выполнения работы
Установить максимальную длину математического маятника l1.
Определить с помощью секундомера время t 20-30Nполных колебаний и вычислить период колебанийТ1=
маятника. Измерение повторить не менее 3 х раз. Углы отклонения маятника должны быть 4 0 – 6 0 .
Поднять шарик на 15-20 см, наматывая нить на барабан, закрепив его стопорным винтом, и определить его длину l2
Определить период колебаний маятника Т2=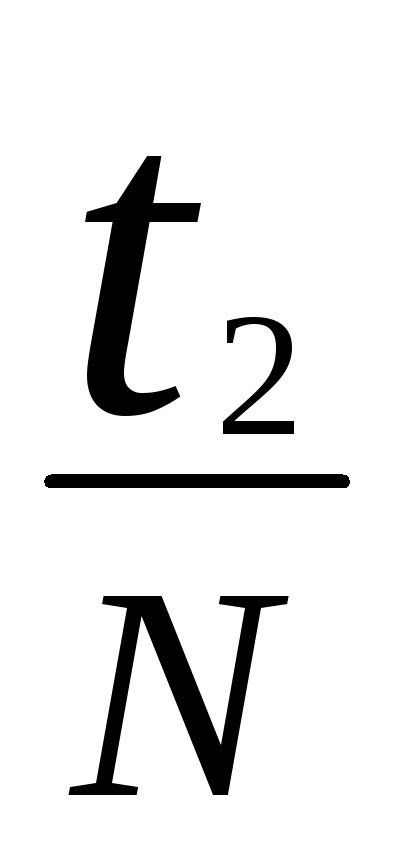
. Измерение произвести не менее 3 х раз.
Рассчитать абсолютную и относительную погрешности ускорения свободного падения и сравнить с g0= 9,81 м/c 2 .
Результаты измерений и вычислений занести в таблицу 5.1.
Какой процесс называется гармоническим колебанием?
Что называется физическим маятником?
Вывести формулу периода математического маятника.
Зависит ли период колебаний математического маятника от его массы.
Почему для определения силы тяжести измеряют периоды и разность длин двух математических маятников, а не используется один маятник, вычисляя g по формуле
g = 4p 2 
6. Вывести формулы погрешностей для всех определяемых величин.
Почему формулой Т = 2p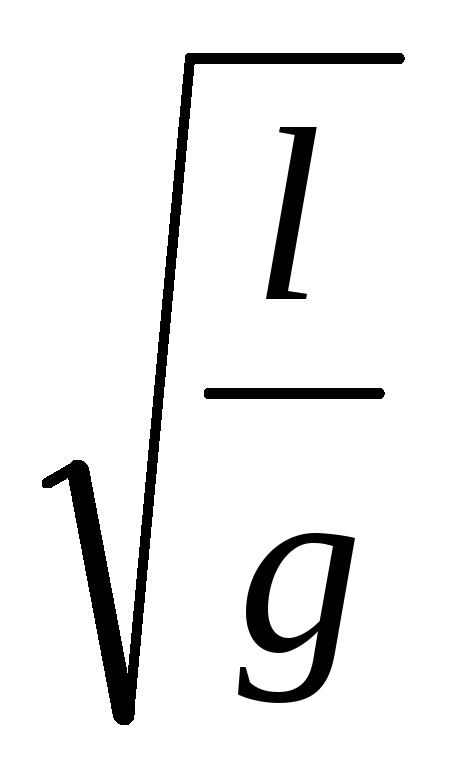
можно пользоваться только в том случае, когда амплитуда колебаний маятника мала?
При работе с математическим маятником следить за тем, чтобы нити не закручивались и не соскальзывали с барабана.
Углы отклонения маятников от положения равновесия не должны превышать 7 0 .
6 Лабораторная работа. Определение отношения теплоемкостей газов по методу клемана и дезорма
Цель работы:определение отношения молекулярной теплоемкости воздуха при постоянном давленииСРк молекулярной теплоемкости при постоянном объеме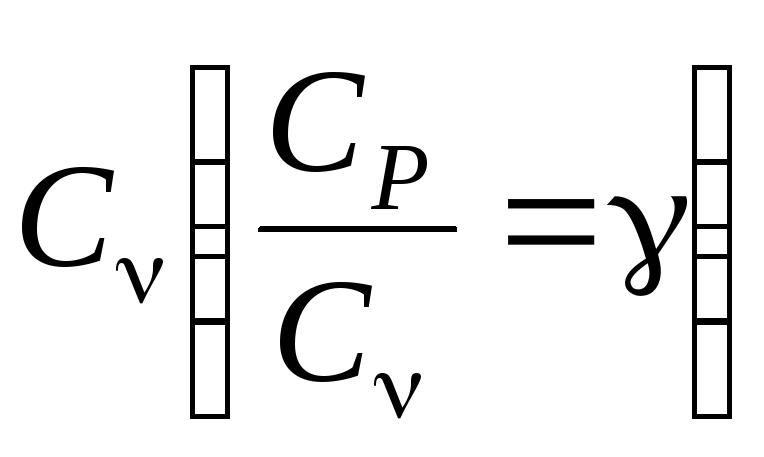
.
6.1 Основные понятия и закономерности
Теплоемкостью вещества называют физическую величину, равную количеству тепла, необходимого для нагревания вещества на один градус 1 °С (или на 1 К).
, (6.1)
где dQ– бесконечно малое количество тепла, полученное веществом,
dT– бесконечно малое изменение (приращение) его температуры.
Теплоемкость зависит от массы нагреваемого тела. Количество тепла, которое надо сообщить единице массы этого вещества, чтобы повысить его температуру на 1 К (или 1 °С) называют удельной теплоемкостьюс:
. (6.2)
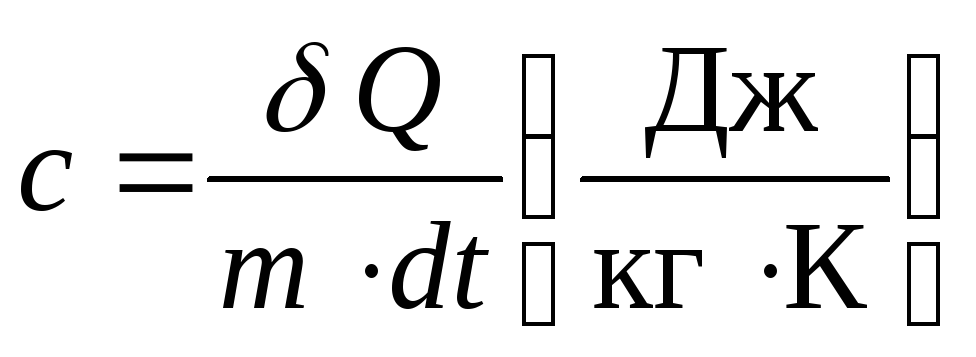
Молярной теплоемкостью Свещества называют физическую величину, численно равную количеству тепла, необходимого для нагревания одногомолявещества на один градус:
, (6.3)
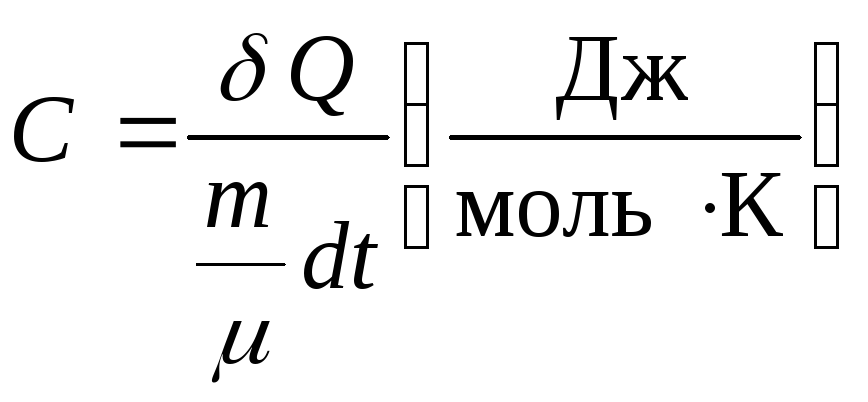
где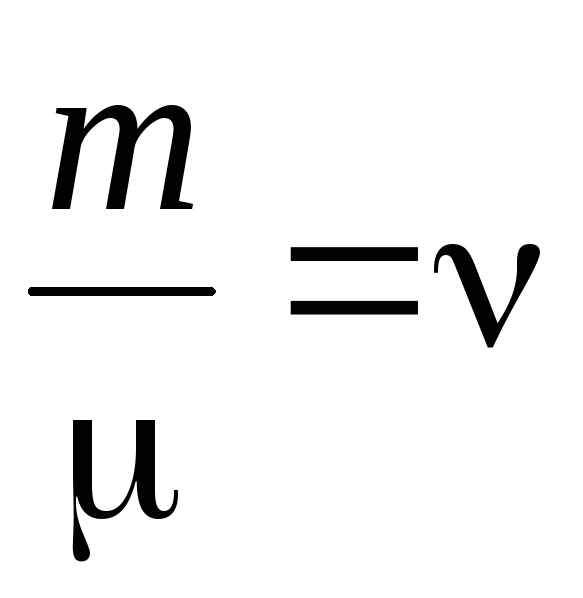 
– количество вещества – числомолейв данной массе.
Из соотношений (6.2) и (6.3) можно определить количество теплоты, получаемое телом:
(6.4)
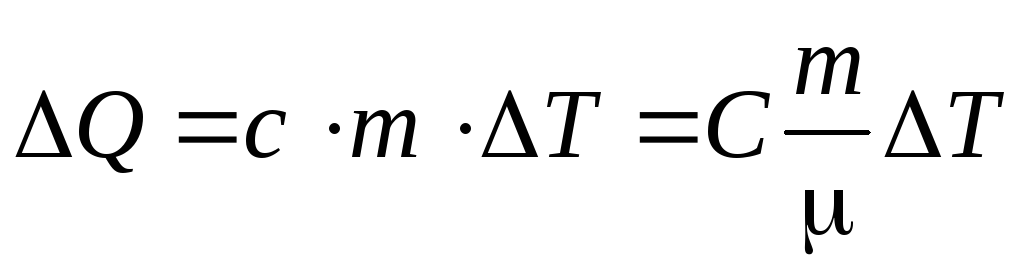
и связь удельной и молярной теплоемкостей сиС:
, (6.5)
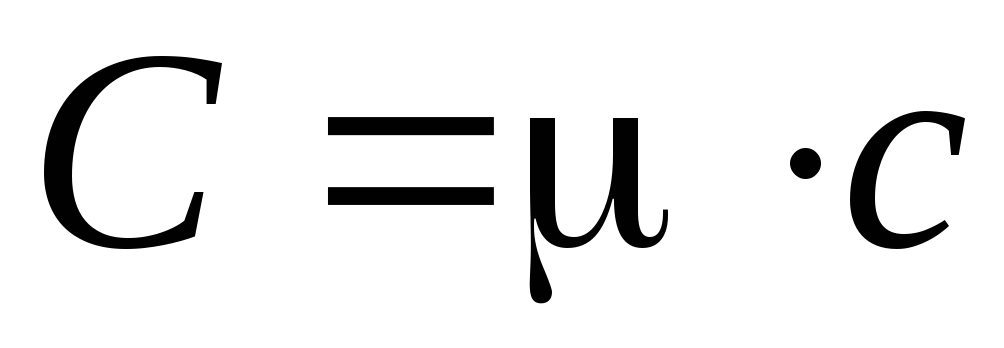
где m– масса одногомолягаза.
У твердых и жидких тел величина теплоемкости не зависит от условий их нагревания.
Теплоемкость газов сильно зависит от условий нагревания. Это связано с тем, что подводимое к газу тепло расходуется не только на повышение внутренней энергии газа, которое обуславливает повышение его температуры, но и на совершение работы против внешних сил.
При нагревании газа при постоянном объеме рассматривается теплоемкость при постоянном объеме СV, при постоянном давленииСP. Чтобы установить различие между теплоемкостямиСpиСV,связь между ними, воспользуемся первым началом (законом) термодинамики – всеобщий закон сохранения и превращения энергии, который формулируется так:количество теплоты dQ, сообщаемое системе, расходуется на увеличение внутренней энергии dU и на совершение системой работы dА над внешними телами (против внешних сил):
, (6.6)
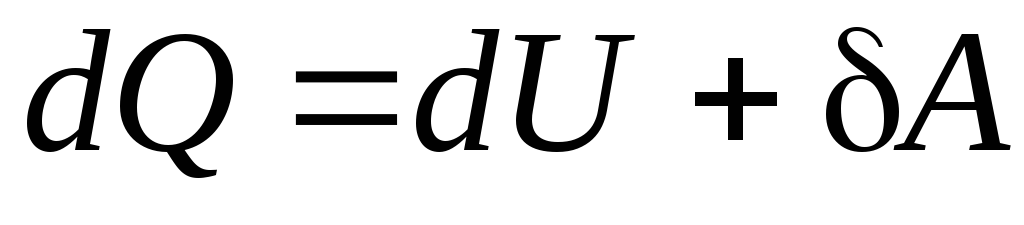
где U– внутренняя энергия системы, т.е. сумма всех видов кинетической и потенциальной энергии всех составных частей системы: молекул, атомов, электронов и т.д.
Для идеального газа внутренняя энергия представляет только кинетическую энергию хаотического, теплового движения молекул и равна:
,
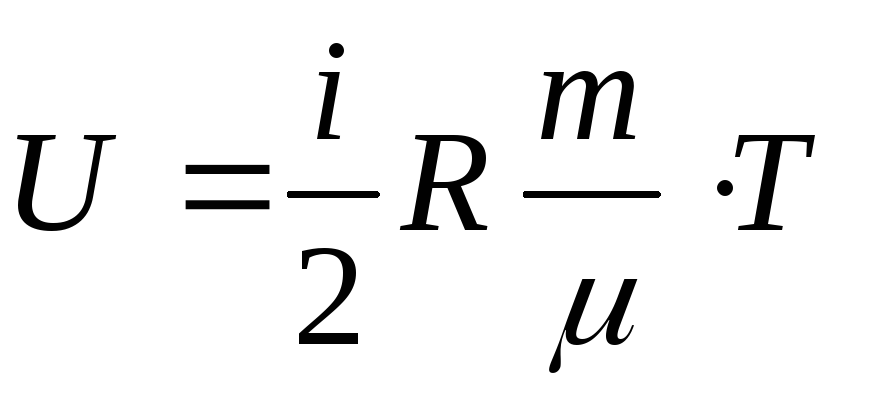
где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),i= 3 для одноатомного газа – поступательные степени свободы,i= 5 для двухатомного газа – три поступательные и две вращательные степени свободы,i= 6 для трех и многоатомных газов – три поступательные и три вращательные степени свободы.
Работа газа против сил внешнего давления равна:
, (6.7)
где P– внешнее давление,
dV– приращение объема газа.
Работа dАи теплотаdQ– две формы передачи энергии от одного тела к другому.
Рассмотрим применение первого начала термодинамики к изопроцессам для данной массы газа. Изопроцессами называются термодинамические процессы, происходящие при постоянном значении одного из параметров состояния (P,V,T).
Изохорический процесс протекает при постоянном объеме V= const, т.е.dV= 0, следовательно,dA=pdV= 0.
Первое начало термодинамики для этого процесса имеет вид:
, (6.8)
Тепло, подводимое к системе, идет на увеличение ее внутренней энергии (нагревание газа) и из соотношения (6.2) равно:
, (6.9)
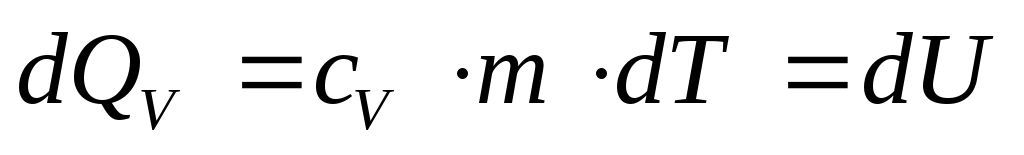
где сV– удельная теплоемкость при постоянном объеме – количество тепла, которое идет на нагревание 1 кг газа на 1 К при постоянном объеме.
Молярная теплоемкость при постоянном объеме CV– теплоемкость одного моля:
, (6.10)
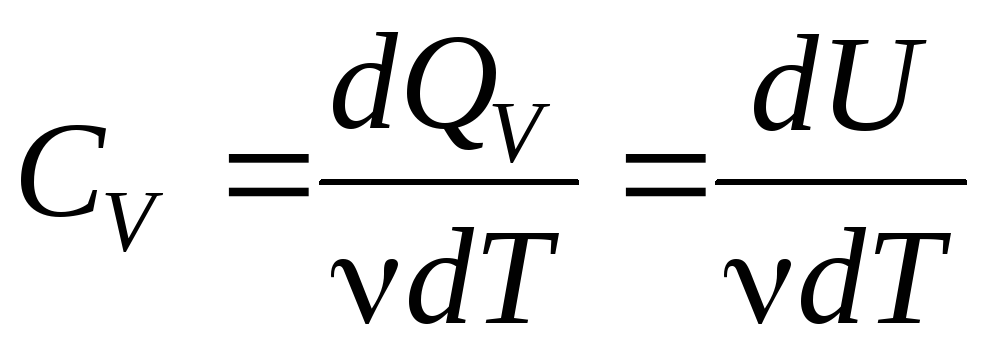
отсюда изменение внутренней энергии для любой массы mравно:
. (6.11)
Приращение внутренней энергии идеального газа равно:
, (6.12)
где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),i= 3 для одно атомного газа – поступательные степени свободы,i= 5 для двух атомного газа – три поступательные и две вращательные степени свободы,i= 6 для трех и много атомных газов – три поступательные и три вращательные степени свободы.
. (6.13)
Изобарический процесс – процесс, протекающий при постоянном давлении Р= const,dP= 0.
Первое начало термодинамики для этого процесса запишется так:
. (6.14)
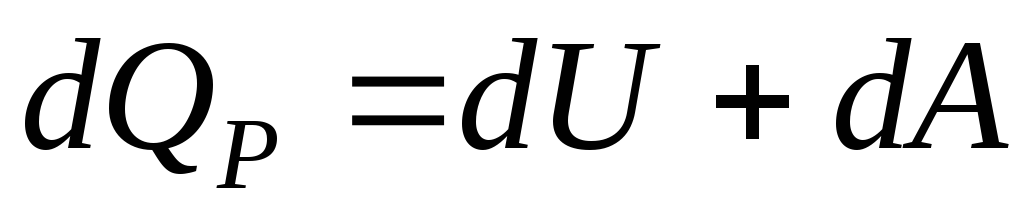
Тепло, подводимое к системе, идет на увеличение внутренней энергии dUи на совершение газом работы над внешними теламиdA=PdV.
Из определения молярной теплоемкости (6.3) имеем:
,
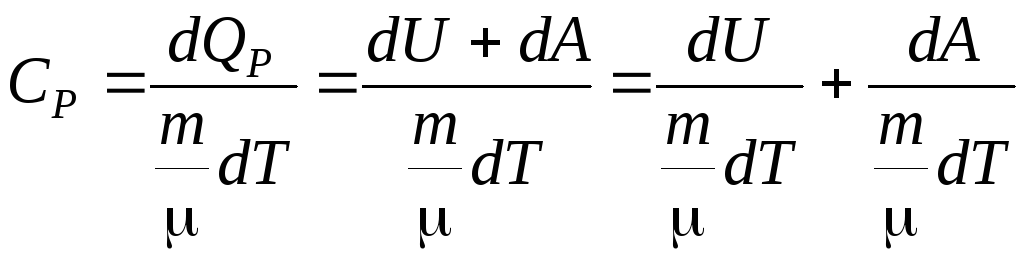
где 
.
. (6.15)
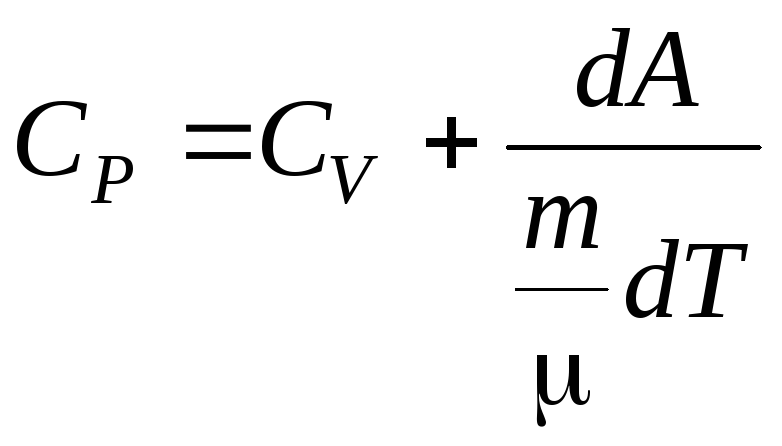
Найдем значение 
для одного моля.
Запишем уравнение Клапейрона-Менделеева для одного моля газа
. (6.16)
Изменение температуры газа при P= const, прямо пропорционально изменению объемаdV, т.е.
,
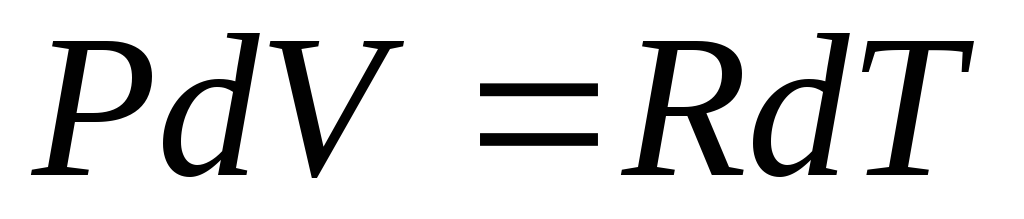
где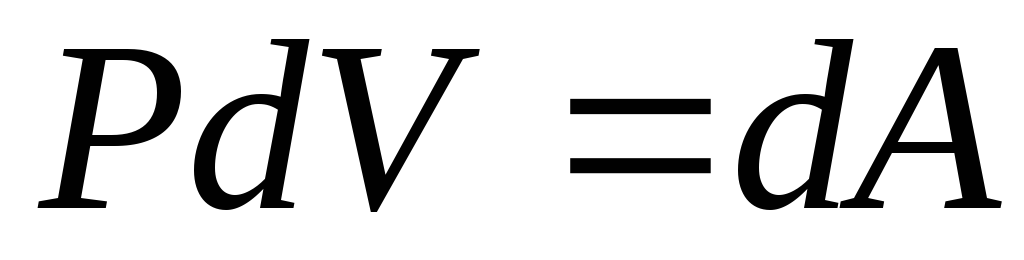 
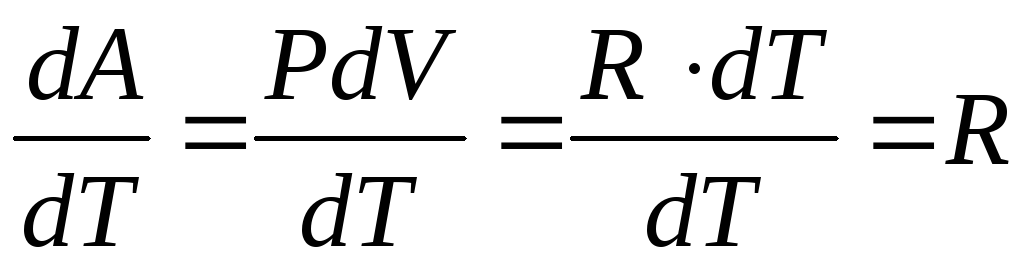
-работа газа.
, (6.17)
где R– универсальная газовая постоянная.
Учитывая, соотношения (6.15) и (6.17), имеем:
(6.18)
– уравнение Майера устанавливает связь между молярными теплоемкостями СРиСV.
Из соотношения (6.17) можно выяснить физический смысл универсальной газовой постоянной – она численно равна работе, совершаемой одним молем газа в результате нагревания на 1 К при постоянном давлении.
Учитывая (6.13) и (6.18), получим:
. (6.19)
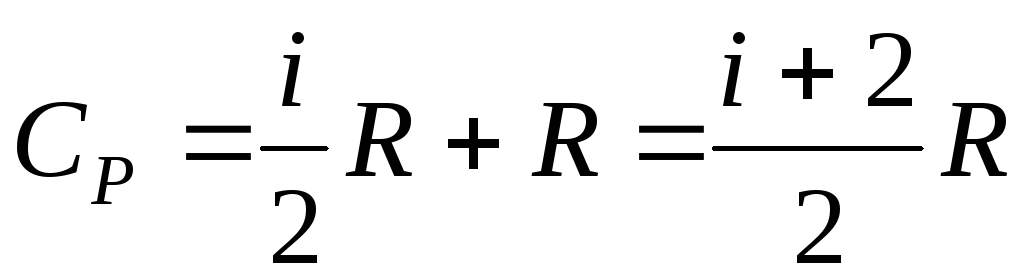
При нагревании 1 моля газа на 1 К при изобарическом процессе часть теплоты CVидет на увеличение внутренней энергии, и часть, равнаяR, – на работу против внешних сил.
Изотермический процесс – процесс, протекающий при постоянной температуре T= const,dT= 0,P×V= const.
Изменение внутренней энергии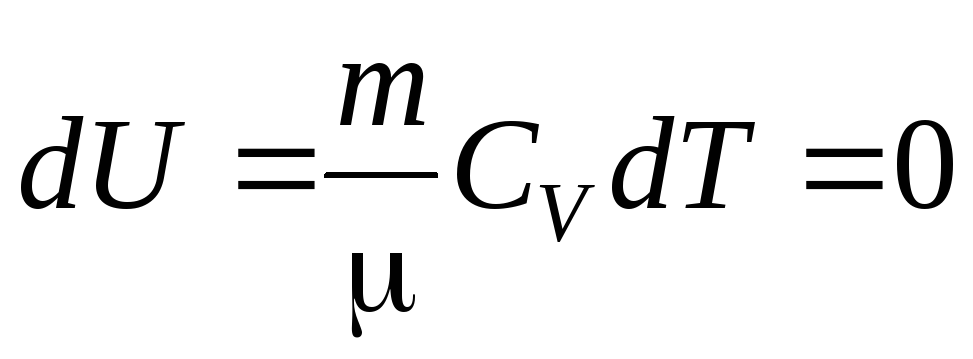 
.
Первое начало термодинамики для этого процесса:
. (6.20)
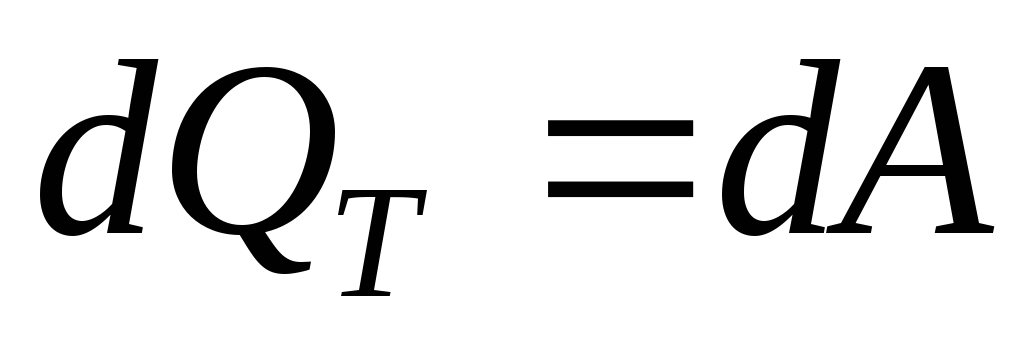
Тепло в этом случае идет только на совершение работы против внешних сил (расширение газа).
В термодинамике, кроме изопроцессов, рассматривается адиабатический процесс.
Адиабатический процесс – процесс, протекающий в условиях полной теплоизоляции, т.е. количество теплоты, получаемое газом равно нулю:
, (6.21)
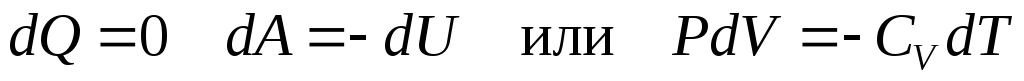
Из первого начала термодинамики следует, что при адиабатическом процессе работа газа над внешними телами совершается за счет уменьшения внутренней энергии. Если объем газа увеличивается, то его температура уменьшается, так как уменьшается его внутренняя энергия.
Для адиабатического процесса имеет место уравнение Пуассона:
, (6.22)
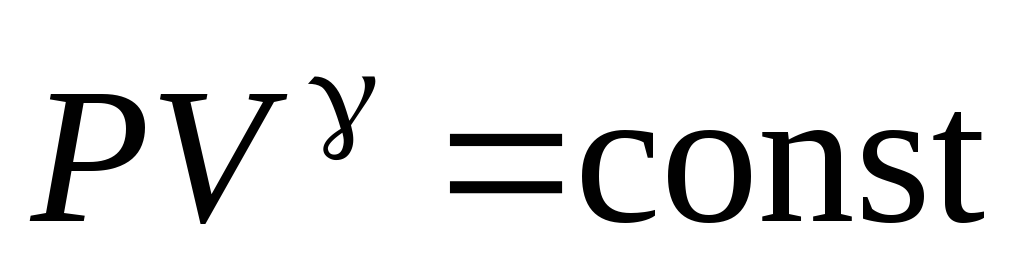
где 
– показатель адиабаты. (6.23)
Уравнение 
для одного моля – первое начало термодинамики в дифференциальной форме. Получим уравнение адиабатического процесса (уравнение Пуассона) в интегральной форме.
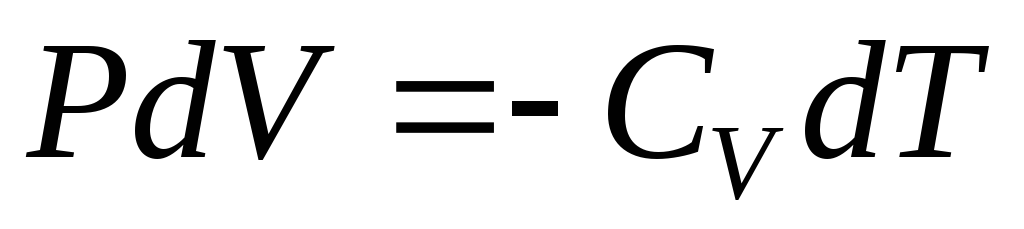
Запишем уравнение Клапейрона-Менделеева для одного моля газа:
(6.24)
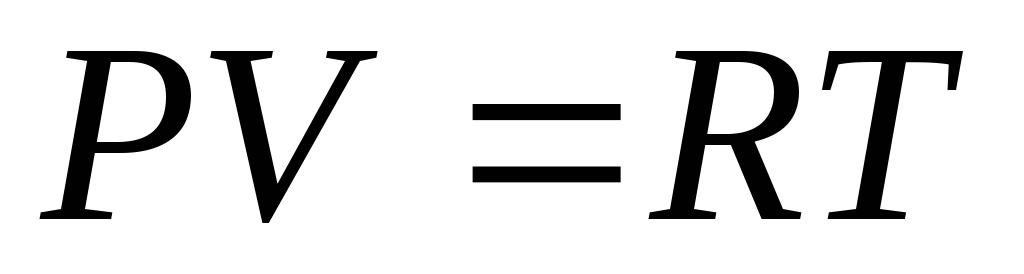
и, дифференцируя это уравнение, имеем:
. (6.25)
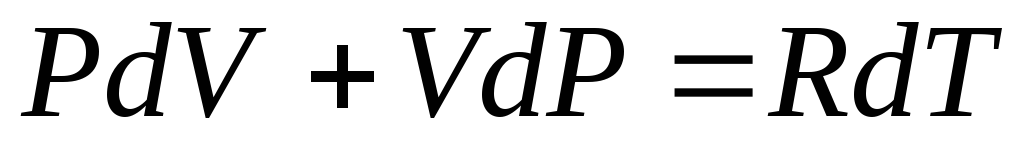
Преобразуем уравнение (6.21) и (6.25), для этого умножим уравнение (6.21) на R, а уравнение (6.25) наCV:
Сложим эти уравнения почленно:
или 
.
Учитывая, что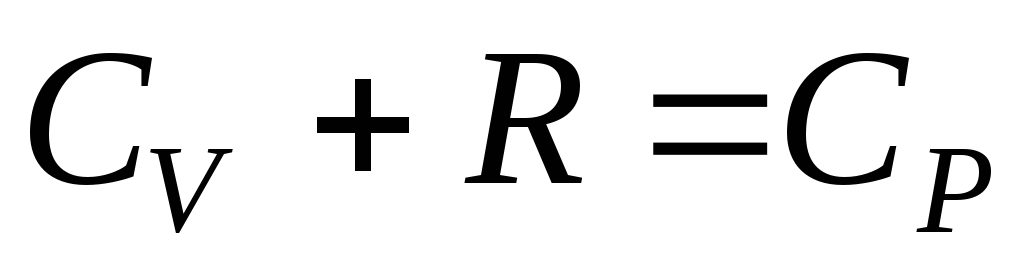 
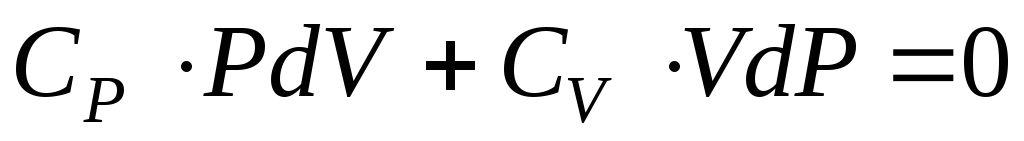
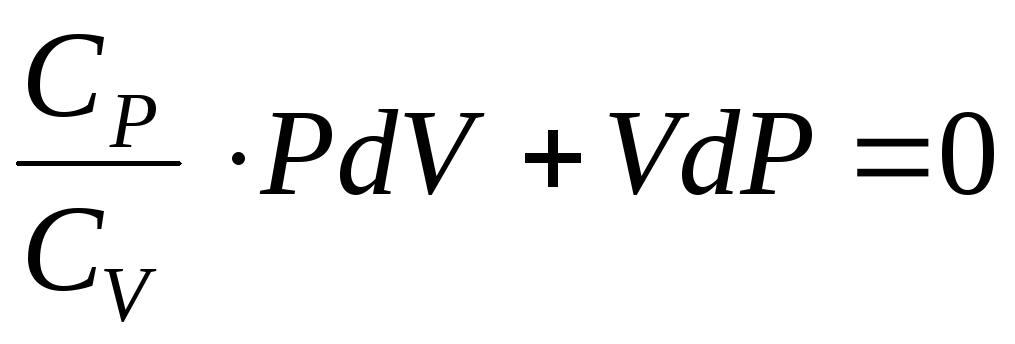
(уравнение Майера), получим:
. (6.26)
,
где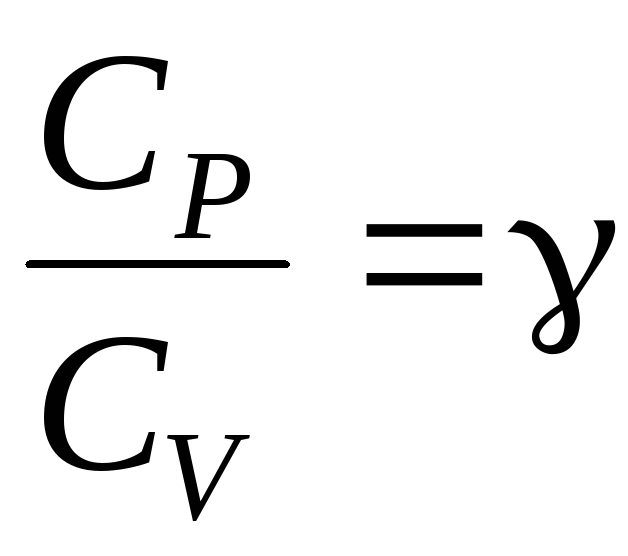 
-показатель адиабаты.
И тогда можно записать:
. (6.27)
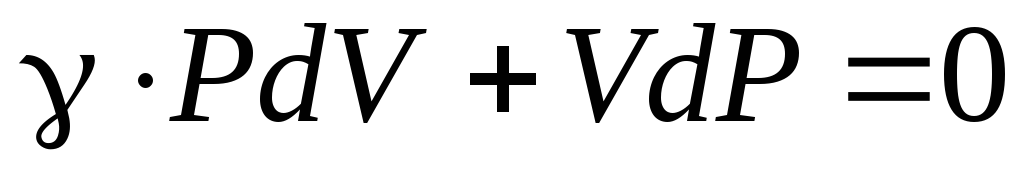
Полученное соотношение является так же, как и (6.21), уравнением адиабаты в дифференциальной форме. Делим обе части этого уравнения на P×V:
, (6.28)
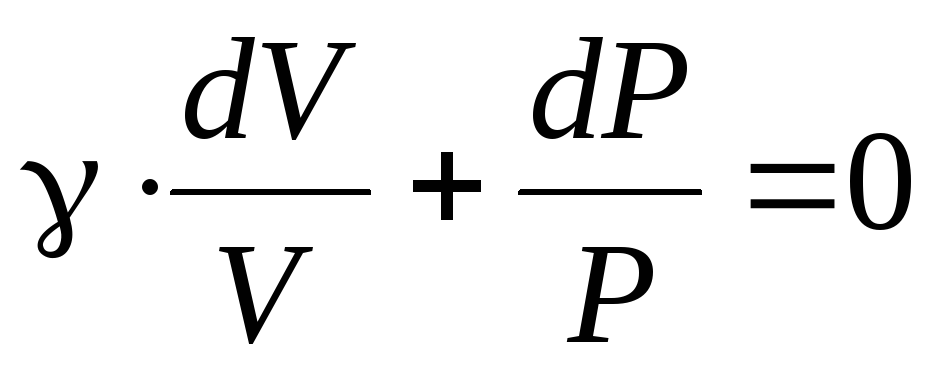
где 
,
, т.е. дифференциалы натуральных логарифмовVиP, поэтому
.
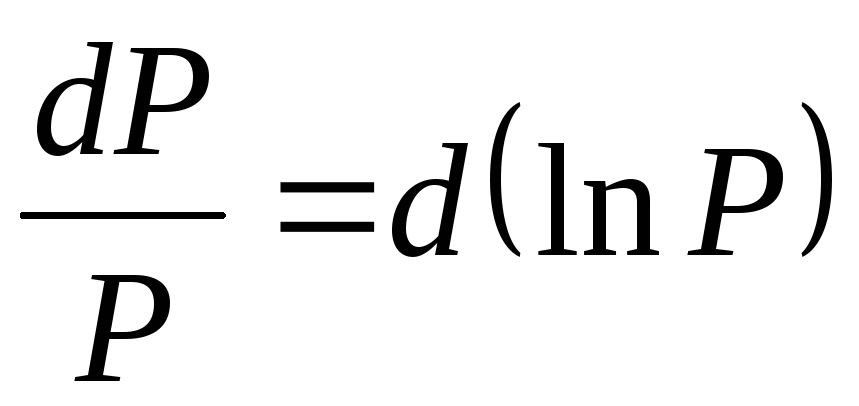
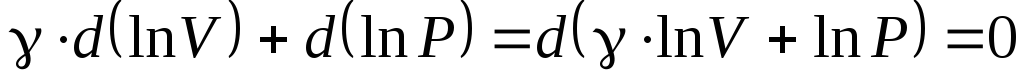
Величина, стоящая в скобках, является постоянной, так как ее дифференциал равен нулю. Обозначим ее (ln const). Тогда можем записать:
. (6.29)
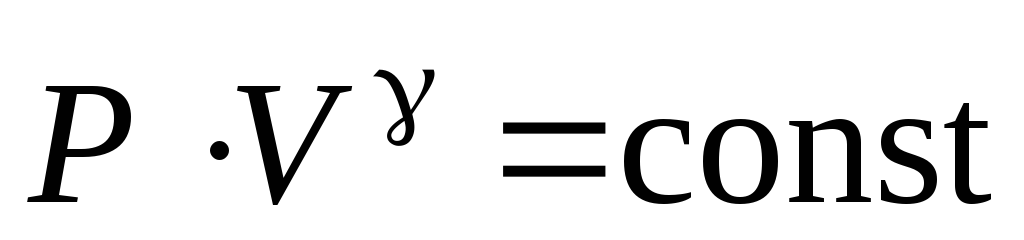
Это соотношение – уравнение адиабаты (Пуассона) (6.22).
Используя соотношения (6.13) и (6.19), можно записать значение показателя адиабаты через степени свободы:
. (6.30)
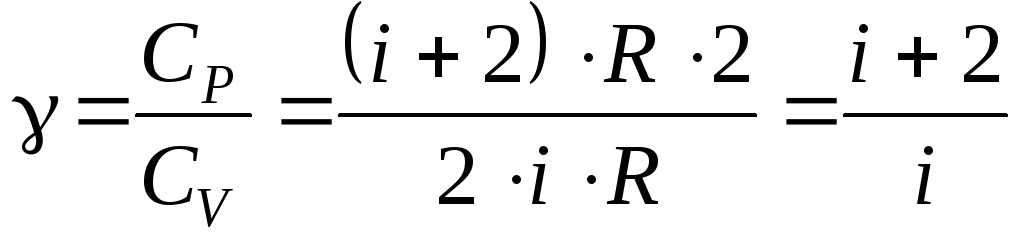
Теория метода и описание установки
6.2.1 Приборы и материалы:баллон с кранами, манометр, насос.
Для определения отношения теплоемкостей в данной работе используется метод, предложенный Клеманом и Дезормом.
У
становка для выполнения работы этим методом состоит из стеклянного баллонаА(рисунок 6.1) емкостью 15¸20 литров, соединенного с манометромВи с насосом (на рисунке не показан). Через кранСбаллонАсоединяется с атмосферой. С помощью кранаДбаллон сообщается с насосом. При открытом кранеСбаллон заполнен воздухом массойm0при атмосферном давленииP0и комнатной температуреT0(состояние 1). На диаграммеP–V(рисунок 6.2) представлена последовательность процессов при выполнении работы. КранСзакрывают и насосом накачивают дополнительную порцию воздухаm.
Давление в баллоне повышается до Р, так как масса газа увеличивается
, состояние 2 (PTV1) (рисунок 6.2).
Температура воздуха увеличивается до T,потому что внешние силы совершают работу по сжатию газа массы m0при накачивании воздуха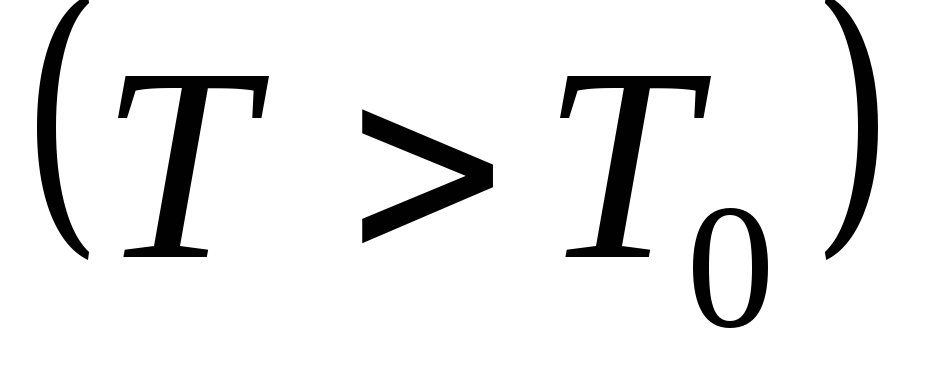
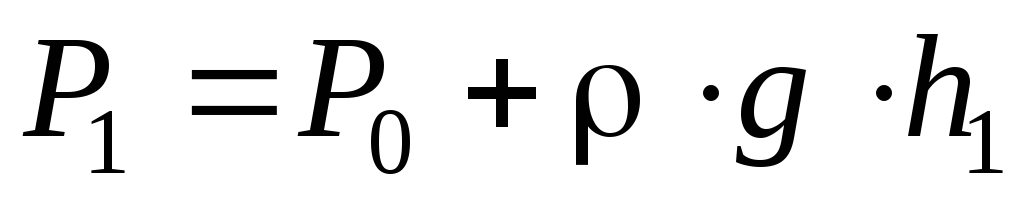
. Вследствие теплообмена воздуха с окружающей средой через некоторое время (2¸3 мин.) температура воздуха, находящегося в баллоне, сравняется с температурой внешней средыT0. При этом по манометру можно отметить уменьшение давление воздуха. Когда температура воздуха в баллоне будет равна комнатной (показания манометра перестанут меняться), давление в баллоне станет равным
, (6.31)
где r×g×h1– избыточное давление воздуха в баллоне,r– плотность жидкости в манометре,h1– разность уровней жидкости в манометре.
Затем кран Соткрывается на короткое время, при этом часть воздуха выходит из баллона, и давление сравнивается с атмосфернымP0. Оставшаяся часть адиабатически расширяется, совершая работу против атмосферного давления; внутренняя энергия газа уменьшается, и температура понижается доT1
Источник
