По векторному способу организации пространственных данных

По векторному способу организации пространственных данных

Растровая модель данных — цифровое представление пространственных объектов в виде совокупности ячеек растра (пикселов) с присвоенными им значениями класса объекта. Р.м. предполагает позиционирование объектов указанием их положения в соответствующей растру прямоугольной матрице единообразно для всех типов пространственных объектов (точек, линий, полигонов и поверхностей).

• Разбивает всю изучаемую территорию на элементы регулярной сетки или ячейки
• Каждая ячейка содержит только одно значение
• Является пространственно заполненной, поскольку каждое местоположение на изучаемой территории соответствует ячейке растра, иными совами — растровая модель оперирует элементарными местоположениями

Соглашения, принятые для растровой ГИС

• Разрешение
  Минимальная линейная размерность наименьшей единицы географического пространства, для которой могут быть приведены какие-либо данные. В растровой модели данных наименьшей единицей для большинства систем выступает квадрат или прямоугольник. Такие единицы известны как сетка, ячейка или пиксель. Множество ячеек образует решетку, растр, матрицу.
• Местоположение
  Наименьшая единица географического пространства, для которого могут быть приведены какие-либо характеристики или свойства (пиксель, ячейка) . Такая частица картографического плана однозначно идентифицируется упорядоченной парой координат — номерами строки и столбца
• Площадной контур (Зона)
  Набор смежных местоположений одинакового свойства. Термин Класс (или район) часто используется в отношении всех самостоятельных зон, которые имеют одинаковые свойства. Основными компонентами зоны являются ее значение и местоположения
• Значение
  Единица информации, хранящаяся в слое для каждого пикселя или ячейки. Ячейки одной зоны (или района) имеют одинаковое значение

Векторная модель данных

Векторно-нетопологическое представление данных (см. модель «спагетти») — цифровое представление точечных, линейных и полигональных пространственных объектов в виде набора координатных пар, с описанием только геометрии объектов.

Векторно-топологическое представление (линейно-узловое представление) — разновидность векторного представления линейных и полигональных пространственных объектов, описывающего не только их геометрию, но и топологические отношения между полигонами, дугами и узлами.

Векторная модель данных:

• Основана на векторах (направленных отрезках прямых)
• Базовым примитивом является точка
• Объекты создаются путем соединения точек прямыми линиями или дугами
• Площади определяются набором линий
• Представляет собой объектно-ориентированную систему

Пример векторного представления пространственных объектов

Типы векторных объектов, основанные на определении пространственных размеров

Безразмерные типы объектов

Точка — определяет геометрическое местоположение

Узел — топологический переход или конечная точка, также может определять местоположение

Одномерные типы объектов

Линия — одномерный объект

Линейный сегмент — прямая линия между двумя точками

Строка — последовательность линейных сегментов

Дуга — геометрическое место точек, которые формируют кривую определенную математической функцией

Связь — соединение между двумя узлами

Направленная связь — связь с одним определенным направлением

Цепочка — направленная последовательность непересекающихся линейных сегментов или дуг с узлами на их концах

Кольцо — последовательность непересекающихся цепочек, строк, связей или замкнутых дуг

Двумерные типы объектов

Область — ограниченный непрерывный объект, который может включать или не включать в себя собственную границу

Внутренняя область — область, которая не включает собственную границу

Полигон (контур) — 2-мерный (площадной) объект, внутренняя область, образованная замкнутой последовательностью дуг в векторно-топологических представлениях или сегментов в модели «спагетти». Различают простой П., не содержащий внутренних П., и составной П, содержащий внутренние П., называемые также «островами» (island) и анклавами (hole).

Пиксель — элемент изображения, который является самым малым неделимым элементом изображения

Пример слоев, составленных из пространственных объектов линейного типа

Примеры слоев, составленных из пространственных объектов полигонального типа

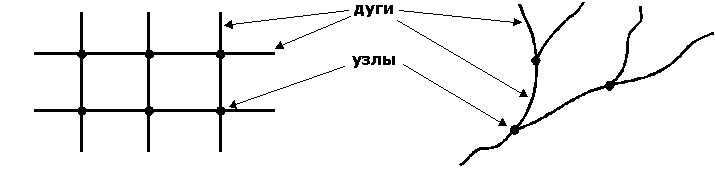
Топологическое представление векторных объектов

Формирование топологии включает определение и кодирование взаимосвязей между точечными, линейными и площадными объектами.

Источник

Векторная модель пространственных данных

Векторный метод представления данных позволяет задавать точные пространственные координаты явным образом. Здесь подразумевается, что географическое пространство является непрерывным, а не разделенным на дискретные ячейки. Это достигается приписыванием точкам пары координат (X и Y) координатного пространства, линиям — связной последовательности пар координат их вершин, областям — замкнутой последовательности соединенных линий, начальная и конечная точки которой совпадают. Векторная структура данных показывает только геометрию картографических объектов. В векторном представлении мы храним в явном виде собственно графические примитивы без атрибутов и полагаемся на связь с отдельной атрибутивной базой данных.

Растровая модель пространственных данных

Квантование, или разбиение пространства на множество элементов, каждый из которых представляет малую, но вполне определенную часть земной поверхности – этот растровый метод может использовать элементы любой подходящей геометрической формы при условии, что они могут быть соединены для образования сплошной поверхности, представляющей все пространство изучаемой области.Растровые структуры данных не обеспечивают точной информации о местоположении, поскольку географическое пространство поделено на дискретные ячейки конечного размера. Вместо точных координат точек мы имеем отдельные ячейки растра, в которых эти точки находятся.

В растровых системах есть два способа включения атрибутивной информации об объектах. Простейшим является присваивание значения атрибута каждой ячейке растра. Распределяя эти значения, мы в конечном итоге позволяем позициям значений атрибутов играть роль местоположений объектов. Например, если числом 10 мы представляем водную поверхность, и записываем его в левую верхнюю ячейку растра, то по умолчанию эта ячейка является участком земной поверхности, представляющим воду. Таким образом мы можем каждой ячейке на данной карте присвоить только одно значение атрибута. Альтернативный подход, а на самом деле, — расширение только что описанного, состоит в связывании каждой ячейки растра с базой данных.

Источник

Тема 4. Организация пространственной информации в ГИС

ТЕМА 4. ОРГАНИЗАЦИЯ ПРОСТРАНСТВЕННОЙ ИНФОРМАЦИИ В ГИС

1. Модели пространственных данных.

Информационную основу ГИС образуют цифровые представ­ления (модели) реальности. С появлением компьютера все множе­ство данных разделилось на два типа: цифровые и аналоговые данные. Последними стали именовать данные на традиционных «бу­мажных» носителях, используя этот термин как антоним цифро­вым данным. В отличие от аналоговой, цифровая форма представ­ления, хранения и передачи данных реализуется в виде цифровых кодов или цифровых сигналов.

Объектом информационного моделирования в ГИС является пространственный объект. Это одно из ключевых понятий геоин­форматики. Он может быть определен как цифровое представле­ние (модель) объекта реальности (местности), содержащее его местоуказание и набор свойств (характеристик, атрибутов), или сам этот объект.

Некоторое множество цифровых данных о пространственных объектах образует пространственные данные. Они состоят из двух взаимосвязанных частей: позиционной (тополого-геометрической) и непозиционной (атрибутивной) составляющих, которые обра­зуют описание пространственного положения и тематического со­держания данных соответственно.

Пространственные объекты как абстрактные представления ре­альных объектов и предмет информационного моделирования (циф­рового описания) в ГИС разнообразны и традиционно классифи­цируются сообразно характеру пространственной локализации ото­бражаемых ими объектов реальности, мерности пространства, ко­торое они образуют, модели данных, используемой для их описа­ния, и по другим основаниям. В рамках объектно-ориентирован­ных моделей данные могут конструироваться в новые классы объек­тов, отличные от базовых или созданных ранее. Базовыми (элемен­тарными) типами пространственных объектов, которыми опери­руют современные ГИС, обычно считаются (в скобках приведены их синонимы) следующие:

точка (точечный объект) – 0-мерный объект, характеризуе­мый плановыми координатами; линия (линейный объект, полилиния) – 1-мерный объект, образованный последовательностью не менее двух точек с извест­ными плановыми координатами (линейными сегментами или ду­гами); область (полигон, полигональный объект, контур, контур­ный объект) – 2-мерный (площадной) объект, внутренняя об­ласть, ограниченная замкнутой последовательностью линий (дуг в векторных топологических моделях (данных) или сегментов в моде­ли «спагетти») и идентифицируемая внутренней точкой (меткой); пиксел (пиксель, пэл) – 2-мерный объект, элемент цифрово­го изображения, наименьшая из его составляющих, получаемая в результате дискретизации изображения (разбиения на далее неде­лимые элементы растра); элемент дискретизации координатной плоскости в растровой модели (данных) ГИС; ячейка (регулярная ячейка) – 2-мерный объект, элемент раз­биения земной поверхности линиями регулярной сети; поверхность (рельеф) – 2-мерный объект, определяемый не только плановыми координатами, но и аппликатой Z, которая входит в число атрибутов образующих ее объектов; оболочка тела; тело – 3-мерный (объемный) объект, описываемый тройкой (триплетом) координат, включающей аппликату Z, и ограничен­ный поверхностями.

Общее цифровое описание пространственного объекта включает:

наименование; указание местоположения (местонахождения, локализации); набор свойств; отношения с иными объектами; пространственное «поведение».

Два последних элемента описания пространственного объекта факультативны.

В зависимости от типа объекта его местоположение определяет­ся парой (триплетом) координат (для точечного объекта) или на­бором координат, организованным определенным образом в рам­ках некоторой модели данных

Это геометрическая часть описания данных, геометрия (метрика) рас­сматриваемых пространственных объектов, отличная от их семан­тики (непозиционных свойств).

Перечень свойств соответствует атрибутам объекта, качествен­ным и количественным его характеристикам, которые приписы­ваются ему в цифровом виде пользователем, могут быть получены в ходе обработки данных или генерируются системой автомати­чески (к последнему типу атрибутов принадлежат, например, зна­чения площадей и периметров полигональных объектов). Суще­ствует расширенное толкование понятия атрибута объекта; после­днему могут быть поставлены в соответствие любые типы данных: текст, цифровое изображение, видео — или аудиозапись, графика (включая карту), что, по существу, реализуется на практике в муль­тимедийных электронных атласах. Под атрибутами понимаются именно содержательные, тематические (непозиционные, непрос­транственные) свойства объектов.

Под отношениями понимают прежде всего топологические свойства (топологию). К топологическим свойствам пространствен­ного объекта принято относить его размерность (мерность, про­странственную размерность), сообразно которой выше были вы­делены 0, 1, 2 и 3-мерные объекты; замкнутость, если речь идет о линейных объектах в широком смысле слова; связность; простота (отсутствие самопересечения линейных объектов и «островов» в полигоне); нахождение на границе, внутри или вне полигона; при­знак точечного объекта, указывающий, является ли он конечным для некоторой линии. Примерами топологических отношений объектов являются их свойства «пересекаться» (или «не пересе­каться»), «касаться», «быть внутри», «содержать», «совпадать», «не совпадать».

Топология вместе с геометрией образует тополого-геометри­ческую часть описания данных, его позиционную часть.

Таким образом, в самом общем виде в пространственных дан­ных следует различать и выделять три составные части: тополо­гическую, геометрическую и атрибутивную – «геометрию», «то­пологию» и «атрибутику» цифровой модели пространственного объекта.

Способы организации цифровых описаний пространственных данных принято называть моделями данных по традиции, унасле­дованной из теоретических обобщений проектирования систем управления базами данных. Они называются также цифровыми пред­ставлениями или просто представлениями пространственных дан­ных.

К основным базовым моделям (представленям) пространственных данных, используемым для описания объектов размерности не более двух (планиметрических объектов) относятся:

растровая модель; регулярно-ячеистая (матричная) модель; квадротомическая модель (квадродерево, дерево квадратов, квадрантное дерево, Q-дерево, 4-дерево); векторная модель:

векторная топологическая (линейно-узловая) модель;

векторная нетопологическая модель (модель «спагетти»).

2. Растровая модель данных.

Модель данных, именуемая растро­вой взамен устаревшего наименования матричной модели данных, имеет аналогии в компьютерной графике, где растр – прямоу­гольная решетка – разбивает изображение на составные однород­ные (гомогенные) далее неделимые части, называемые пикселами (от английского pixel, сокращение от «picture element» – элемент изображения), каждому из которых поставлен в соответствие не­который код, обычно идентифицирующий цвет в той или иной системе цветов (цветовой модели). Из множества значений логи­ческих пикселов складывается цифровое изображение. Растровая модель данных в ГИС предполагает разбиение пространства (коор­динатной плоскости) с вмещающими ее пространственными объек­тами на аналогичные пикселам дискретные элементы, упорядо­ченные в виде прямоугольной матрицы. Для цифрового описания (позиционирования) точечного объекта при этом будет достаточ­но указать его принадлежность к тому или иному элементу дискре­тизации, учитывая, что его положение однозначно определено но­мерами столбца и строки матрицы (при необходимости координа­ты пиксела, либо его центроида или любого угла могут быть вы­числены). Пикселу присваивается цифровое значение, определяю­щее имя или семантику (атрибут) объекта. Аналогичным образом описываются линейные и полигональные объекты: каждый эле­мент матрицы получает значение, соответствующее принадлеж­ности или непринадлежности к нему того или иного объекта.

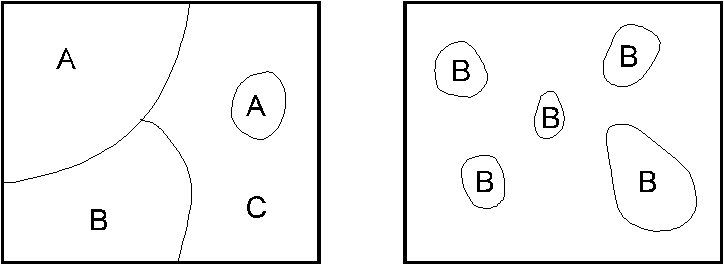
Рис. 6. Растровая модель данных Исходные полигональные объекты (а) с атрибутами (классами) Л, В, С, D и Е и матрица размером 7×7 растро­вой модели (о), каждому элементу которой присвоено значение атрибу­та объекта | Картография. 1994. – С. 198|

Выбрав подходящий размер пиксела растровой модели, можно добиться пространственного разреше­ния (точности представления объектов), удовлетворяющего целям их цифрового описания и последующей обработки, если этому не препятствуют соображения экономии машинной памяти: двукратное увеличение разрешения ведет к четырехкратному росту объе­мов хранимых данных и т. д. Полученная матрица образует растро­вый слой с однотипными объектами; множество разнотипных объек­тов образует набор слоев, составляющих полное цифровое описа­ние моделируемой предметной области. С каждым семантическим значением или кодом пиксела, кроме того, может быть связан неограниченный по длине набор (таблица) атрибутов, каждый из которых можно развернуть в производный слой, соответствующий размеру исходной матрицы. Таким образом, становится не столь обязательным разделение данных на позиционную и семантичес­кую составляющие, отпадает необходимость в особых средствах хранения и манипулирования метрикой и семантикой простран­ственных данных, как это принято в векторных системах, суще­ственно упрощаются аналитические операции, многие из которых (включая обработку запросов с логическими условиями) сводятся к попиксельным операциям с набором растровых слоев, которые могут быть легко «распараллелены».

В ГИС растрового типа (с возможностями поддержки растровой модели данных) достаточно просто могут быть реализованы фун­кции их обработки, включая пространственный анализ. Зачастую они содержат также аппарат, получивший название «картографи­ческой алгебры» (неудачный дословный перевод с английского «тар algebra»), аналогичный по языковым средствам матричным опера­циям в некоторых языках программирования. Поддержка растро­вой модели данных – хорошая предпосылка (и условие) интегра­ции программных продуктов ГИС со средствами цифровой обра­ботки данных дистанционного зондирования и обработки изобра­жений в целом.

Простота машинной реализации операций с растровыми дан­ными находится в противоречии с другой главной их особеннос­тью – значительными затратами машинной памяти, требуемой для их хранения (в сравнении с объемами данных в векторных моделях).

3. Регулярно-ячеистая модель данных.

Описанная выше растровая модель данных пригодна для цифрового представления не только пространственных объектов в ГИС, но и изображений, например, цифровые фотоизображения, снятые непосредствен­но цифровой фотокамерой или полученные путем цифрования аналоговых негативов или фотоотпечатков на сканере. Или цифровые аэроснимки и космические снимки, получаемые с борта космических плат­форм и других летательных аппаратов. Или оцифрованную на том же сканере бумажную карту.

Во всех перечисленных выше случаях речь идет о цифровых ра­стровых изображениях, образованных множеством его элементов – пикселов, каждому из которых ставится в соответствие значение (код) цвета или спектрального коэффициента яркости объекта съемки. На эти далее неделимые элементы растра «разбивается» и координатная плоскость с пространственными объектами в их ра­стровом представлении. Если атомарной единицей данных при их описании служит элемент «разбиения» территории – регулярная пространственная ячейка (территориальная ячейка) правильной геометрической формы – речь идет о другой, отличной от растро­вой, хотя и формально с нею схожей, регулярно-ячеистой модели данных. Формальное сходство абсолютно в случае квадратной (пря­моугольной) формы ячеек, хотя известны примеры регулярных (или квазирегулярных) сетей (решеток) с ячейками правильной тре­угольной, гексагональной или трапециевидной формы, равновели­ких или квазиравновеликих.

При этом сеть может строиться (разу­меется мысленно) на плоскости в условных прямоугольных коор­динатах некоторой картографи­ческой проекции или на повер­хности шара или эллипсоида; в последнем случае регулярными ячейками обычно являются сфе­рические трапеции фиксирован­ного или переменного углового размера.

Рисунок – Разбиение сферы на равновеликие трапеции

Представление данных на основе регулярных пространствен­ных сетей образует основу глобальных цифровых моделей рельефа (ЦМР) Земли.

4. Квадротомическая модель данных.

Актуальность исполь­зования этой модели и поддержки её программными средствами ГИС заключается в компакт­ности по сравнению с растровой моделью, расточительной по объе­мам машинной памяти, требуемой для хранения растровых дан­ных. Свойством эффективно уменьшать количество данных по сравнению с растровой моделью при сохранении быстрого доступа к элементам описания пространствен­ных объектов обладает квадротомическая модель данных, основан­ная на подходе, известном как квадротомическое дерево (квадродерево). В его основе лежит разбиение территории или изображе­ния на вложенные друг в друга пикселы или регулярные ячейки с образованием иерархической древовидной структуры – декомпо­зиции пространства на квадратные участки (квадраты, квадратные блоки, квадранты), каждый из которых делится рекурсивно на четыре вложенных до достижения некоторого уровня простран­ственного разрешения. Механизм построения квадродерева исход­ного участка территории с пятью областями (полигонами), кото­рому в растровом представлении соответствовал бы рис. 10, в ре­зультате его последовательной (рекурсивной) декомпозиции на квадранты показан на рис. 11.

На первом этапе деления исходного участка на четыре квадрат­ных блока (см. рис. 11) и одновременном «ветвлении» квадродере­ва (рис. 12) образуется один неделимый далее элемент № 1 (ему соответствует «лист» дерева на рис. 12) и три «узла» делимых далее квадратов первого уровня иерархии (принимая «корневой» уро­вень квадратного участка в целом за нулевой). За исключением де­вяти гомогенных квадратов на втором иерархическом уровне все остальные элементы делятся далее, пока необходимость дальней­шего деления не будет исчерпана на последнем четвертом этапе. Экономия в сравнении с растровой моделью данных очевидна – область Е оказалась представленной одним квадратом под номе­ром 33 (а не 16 элементами растра или ячеек регулярной сети), и ее цифровое описание подразумевает лишь формализованное представление структуры квадродерева. Обычно оно строится на осно­ве так называемой матрицы Мортона, определяющей оптимальный в некотором смысле порядок ее кодирования и физической записи, обеспечивая минимальный последовательный поиск.

Линейная квадротомическая модель данных практически реа­лизована в немногих из известных программных средств ГИС. Ее не следует путать с так называемыми пирамидальными моделями, также рекурсивно организуемыми и используемыми при обработ­ке цифровых изображений, включая данные дистанционного зон­дирования. В отличие от квадродерева, они представляют собой набор растровых слоев изображений с механически двукратно уменьшаемым разрешением, а потому более компактных, искус­ственно «загрубленных» в целях их быстрого воспроизведения.

Известны трехмерные расширения линейной квадротомической модели – это так называемая октотомическая модель (модель октарного дерева) как результат рекурсивного деления трехмерного пространства на восемь октантов, используемая для цифрового описания тел.

Предлагалась также модель трихотомического дерева с анало­гичным квадратомическому делению треугольных элементов.

5. Векторные модели данных.

В отличие от занимающих все пространство растровых моде­лей векторные модели данных строятся на линиях, занимающих часть пространства. Это определяет основное преимущество вектор­ных моделей, которое заключается в том, что им требуется на поряд­ки меньшая память для хранения и меньшие затраты времени на обработку и представление. Они используются для цифрового представления точечных, линейных и площадных (полигональных) объектов, имея аналогии в картографии, где различаются объекты с точечным, линейным и площадным характером пространствен­ной локализации

Векторные модели получают разными способами. Один из наи­более распространенных — векторизация сканированных (растровых) изображений то есть с помощью техно­логий цифрования карт, планов и другой графической доку­ментации с помощью устройств ввода векторного типа – диги­тайзеров (цифрователей) с ручным обводом, генерирующих по­ток пар плановых координат (векторов) вслед за движением кур­сора (обводной головки) по планшету дигитайзера при отслежи­вании и записи графических объектов помещенного на него ори­гинала. Другой способ — построение модели в режиме редактирования.

При построении векторных моделей объекты создаются путем соединения точек прямыми линиями, дугами, полилиниями. Пло­щадные объекты в векторных моделях задаются наборами линий.

Геоинформационные системы, работающие с векторными мо­делями, получили название векторных ГИС.

Конечно в реальности имеют дело не с абстрактными линиями и точками, а с объектами, содержащими линии и ареалы, занимаю­щими пространственное положение, а также со сложными взаимо­связями между ними. Поэтому полная векторная модель данных отображает пространственные данные как совокупность следующих основных частей:

геометрические (метрические) объекты (точки, линии и поли­гоны); атрибуты — признаки, связанные с объектами; связи между объектами.

Векторные модели отображают все типы координатных моде­лей: точечные, линейные, площадные. Типы координатных моделей определяются через базовый элемент линия сле­дующим образом.

Точка определяется как линия нулевой длины. Линия — как ли­ния конечной длины. Площадь представляется последовательностью связанных между собой линейных отрезков.

Векторные модели могут иметь любую заданную ширину ли­ний, включая нулевую. В этом их преимущество перед растровыми, в которых точечный или линейный объект должен занимать группу ячеек. Это создает зависимость размеров растрового объекта от величины растра.

Поэтому точность векторных данных выше, чем растровых, так как векторные данные могут кодироваться с любой мыслимой сте­пенью точности, которая ограничивается лишь возможностями метода внутреннего представления координат.

Не все природные явления имеют характерные четкие грани­цы, которые можно представить в виде математически определенных линий. Это обусловлено динамикой явлений или способами сбора пространственной информации. Почвы, типы растительности, скло­ны, место обитания диких животных — все эти объекты не имеют четких границ.

Поэтому для полного изучения явлений окружающей действи­тельности нужно использовать как векторные так и растровые дан­ные, используя их преимущества.

Векторные модели делятся на две группы: векторные топологические (линейно-узловые) и векторные нетопологические (модели «спагетти»).

Простейшей векторной структурой данных является спагетти-модель, приведенная, которая по сути переводит один в один графическое изображение карты. Суть её заключается в следующем: если представить себе покрытие каждого графического объекта (каждой линии) бумажной карты кусочком (одним или несколькими) макарон, то вы получите достаточно точное изображение того, как эта модель работает. Каждый кусочек действует как один примитив: очень короткие – для точек, более длинные – для отрезков прямых, наборы отрезков, соединенных концами, – для границ областей. Каждый примитив – одна логическая запись в компьютере, записанная как строки переменной длины пар координат (X, Y). В этой модели соседние области должны иметь разные цепочки спагетти для общих сторон. То есть, не существует областей, для которых какая-либо цепочка спагетти была бы общей. Каждая сторона каждой области имеет свой уникальный набор линий и пар координат. Хотя, конечно, общие стороны областей, даже будучи записанными отдельно в компьютер должны иметь одинаковые наборы координат.

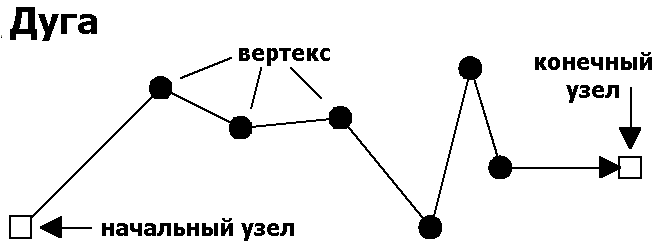
В отличие от спагетти-модели, топологические модели, как это следует из названия, содержат топологическую информацию в явном виде. С ней связаны и особые термины, от­ражающие ее структуру; главные ее элементы (примитивы):

промежуточная точка; сегмент (линейный сегмент, отрезок (прямой)); узел; дуга; полигон (область, полигональный объект, многоугольник, кон­тур, контурный объект), в том числе:

простой полигон; внутренний полигон («остров», анклав); составной полигон; универсальный полигон (внешняя область).

Описание полигона в векторной топологической модели – это множество трех элементов: узлов, дуг и собственно полигонов. Меж­ду этими объектами устанавливаются некоторые топологические отношения, необходимым элементом которых должна быть связь дуг и узлов, полигонов и дуг.

Топологическая информация описывается набором узлов и дуг. Узел — больше, чем просто точка, обычно это пересечение двух или более дуг, и его номер используется для ссылки на любую дугу, которой он принадлежит. Каждая дуга начинается и заканчивается либо в точке пересечения с другой дугой, либо в узле, не принадлежащем другим дугам. Дуги образуются последовательностями отрезков, соединенных промежуточными (формообразующими) точками. В этом случае каждая линия имеет два набора чисел: пары координат промежуточных точек и номера узлов. Кроме того, каждая дуга имеет свой идентификационный номер, который используется для указания того, какие узлы представляет ее начало и конец. Области, ограниченные дугами, также имеют идентифицирующие коды, которые используются для определения их отношений с дугами. Далее, каждая дуга содержит явную информацию о номерах областей слева и справа, что позволяет находить смежные области. Эта особенность данной модели позволяет компьютеру знать действительные отношения между барическими объектами. Другими словами, эта векторная модель данных лучше отражает то, как пользователи карт, определяют пространственные взаимоотношения, записанные в традиционном документе.

Источник