По способу выражения погрешности средств измерений могут быть классифицированы как

Классификация погрешностей.

№	Признак	Виды погрешностей
Измерений	Средств измерений
По способу выражения	Абсолютная Относительная	Абсолютная Относительная Приведенная
По источнику возникновения	Методическая Инструментальная Субъективная	Инструментальная
По характеру проявления	Систематическая Случайная Грубая (промах)	Систематическая Случайная
В зависимости от условий применения СИ	–	Основная Дополнительная
В зависимости от характера поведения измеряемой физической величины в процессе измерения	–	Статическая Динамическая
По характеру зависимости от измеряемой величины	–	Аддитивная Мультипликативная

1. По способу выражения различают абсолютную, относительную и приведенную погрешность.

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины и определяемая согласно выражения (1.2). Абсолютная погрешность сама по себе не может служить показателем точности измерений, так как одно и то же ее значение, например Δ = 0,05 мм, при X = 100 мм соответствует довольно высокой точности измерений, а при X = 1 мм – низкой.

Поэтому вводится понятие относительной погрешности.

Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности к действительному значению. Во многих случаях она является более наглядной характеристикой оценки качества результата измерения. Относительную погрешность δ находят из выражения

(1.3)

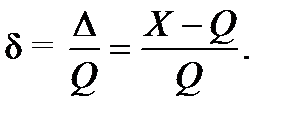
Относительную погрешность выражают в относительных единицах или в процентах (в последнем случае в формуле (1.3) к правой части добавляется множитель 100 %).

Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерений отнесена к условно принятому значению Х_N, постоянному на всем диапазоне измерений или его части:

(1.4)

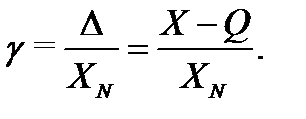
где X_N – нормирующее значение. За нормирующее значение часто принимают верхний предел измерений. Указание погрешности измерений в виде относительной приведенной погрешности говорит о том, что абсолютная погрешность измерений Δ постоянна на всем диапазоне (поддиапазоне) измерений.

2. По причине возникновения различают методическую, инструментальную и субъективную погрешности.

Методическая погрешность (Δ_м) – это составляющая систематической погрешности измерения, возникающая из-за несовершенства принятого метода измерения. Эта погрешность, в основном, проявляется как систематическая погрешность, но иногда может проявляться как случайная методическая погрешность, например погрешность, обусловленная влиянием повторной установки объекта измерения на измерительную позицию, влиянием дискретности измеряемой ФВ и др.

Примеры: 1. Влияние радиационного нагрева при измерении температуры термометром, размещенным на солнце.

2. Влияние входного сопротивления вольтметра на результат измерения напряжения.

Инструментальная погрешность(Δ_инс) – это составляющая погрешности измерения, обусловленная погрешностью применяемого СИ. Например, инструментальная погрешность может быть обусловлена нелинейностью преобразования сигнала, ограниченностью динамического диапазона, инерционностью СИ, изменением условий эксплуатации (температуры окружающей среды, электромагнитными помехами, колебаниями напряжения в сети питания). Инструментальная погрешность складывается из основной и дополнительных погрешностей.

Субъективная погрешность(Δ_суб) – это составляющая систематической погрешности измерения, обусловленная индивидуальными особенностями оператора. Например, при отсчитывании показаний СИ в аналоговом виде большое значение имеет правильное расположение оператора по отношению к показывающему устройству. Некоторые операторы систематически опаздывают с отсчетом показаний.

3. По характеру проявления различают систематическую, случайную и грубую погрешности.

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности могут быть предсказаны, обнаружены и исключены (уменьшены) из результата измерений введением поправок. Например: погрешности от измерения температуры и др. влияющих факторов. Погрешности такого рода являются не изменяющимися во времени функциями вызывающих их влияющих величин (температуры, частоты, напряжения и пр.).

Поправки всегда определяются и вычисляются с некоторой погрешностью, часть систематических погрешностей так или иначе оказывается необнаруженной, поэтому существует понятие неисключенная систематическая погрешность (НСП). Иногда этот вид погрешности называют неисключенными остатками систематической погрешности, остающимися после введения поправок и содержащимися в результате измерений.

В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодическиеипогрешности, изменяющиеся по сложному закону.

Постоянные погрешности – погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.

Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.

Периодические погрешности – погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.

Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.

Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений физической величины постоянного размера, проведенных с одинаковой тщательностью в одинаковых условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они проявляются при повторных наблюдениях в виде некоторого разброса полученных результатов. Случайные погрешности неустранимы и всегда присутствуют в результате измерения. Описание предельных значений случайных погрешностей возможно на основе теории случайных процессов и математической статистики. Уменьшение случайных погрешностей возможно путем увеличения числа наблюдений.

Грубая погрешность (промах) – это погрешность, которая при исправных средствах измерений и корректных действиях экспериментатора (оператора) не должны появляться. Причина промахов – ошибки оператора, сбои в работе аппаратуры, скачки напряжения в сети, вибрация и т. п. Промахи проявляются они в том, что результаты отдельных измерений резко отличаются от остальных. При однократном измерении промах может быть обнаружен только путем логического анализа или сопоставления результата с априорным представлением о нем. Если причина промаха установлена, то результат однократного измерения следует признать ошибочным и повторить измерение. При многократном измерении одной и той же величины постоянного размера промахи проявляются в том, что результаты отдельных измерений, входящих в один ряд, резко отличаются от остальных результатов этого ряда. Такие промахи выявляют с помощью специальных критериев при обработке результатов измерений.

4. В зависимости от условий применения СИ различают основную и дополнительную погрешности.

Основная погрешность СИ – это погрешность СИ, применяемого в нормальных условиях.

Дополнительная погрешность СИ – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений. Примеры: дополнительные погрешности, вызванные изменением температуры окружающей среды, напряжения питания и др.

Дополнительные погрешности нормируют функциями влияния, которые могут иметь вид числа, формулы, таблицы или графика. В частности, дополнительная погрешность от изменения температуры окружающей среды может указываться в виде коэффициента, равного значению дополнительной погрешности, возникающей при изменении температуры на 1 или 10 °С, например: ±0,01 %/°С.

5. В зависимости от постоянства измеряемой величины различают статическую и динамическую погрешности.

Статическая погрешностьСИ – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.

Динамическая погрешность СИ – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины. Эта дополнительная динамическая составляющая погрешности обусловлена инерционными свойствами СИ, не способного отслеживать быстрое изменение измеряемой ФВ. Примерами динамических измерений являются измерения мгновенных значений быстро протекающих процессов.

Дата добавления: 2016-02-13 ; просмотров: 6020 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Погрешность измерений. Классификация

Погрешность средств измерения и результатов измерения.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности.

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Систематическая и случайная погрешности.

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
погрешность градуировки или небольшой сдвиг шкалы;
неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
неравномерный износ направляющих устройств для базирования измеряемых деталей;
износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
усталостные измерения упругих свойств деталей, а также их естественное старение;
неисправности средства измерений.

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0. 100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30. 100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50. +50, Xn=100).

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Источник