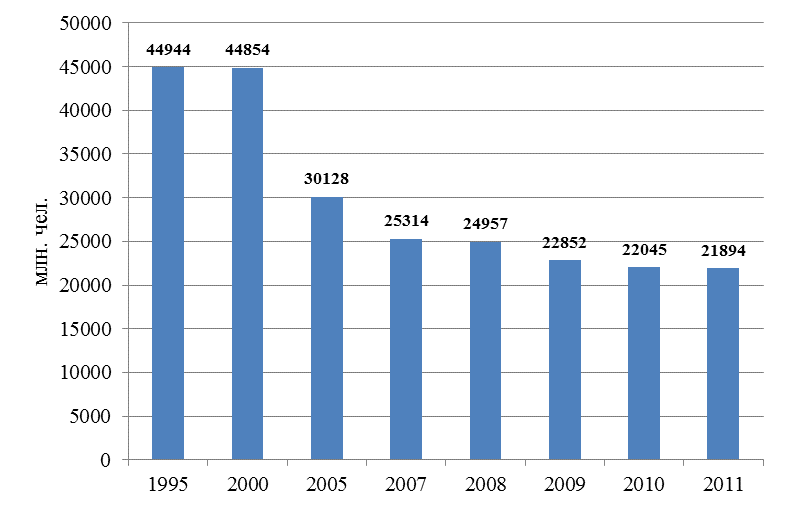Классификация статистических графиков
Для графического изображения статистических данных используются самые разнообразные виды графиков. При всем своем разнообразии статистические графики классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач (цели использования) (рис. 5.3; 5.4).
1) По способу построения:
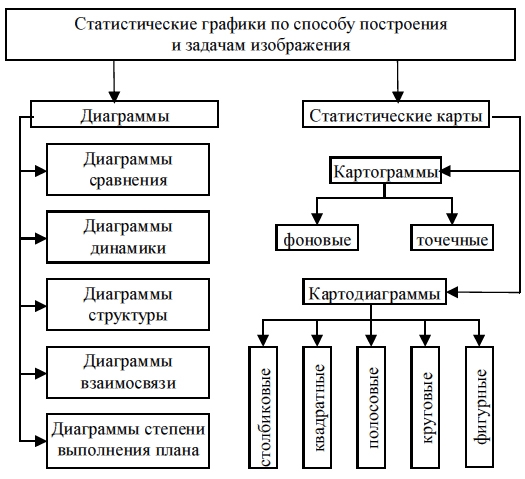
— статистические карты: картограммы и картодиаграммы;
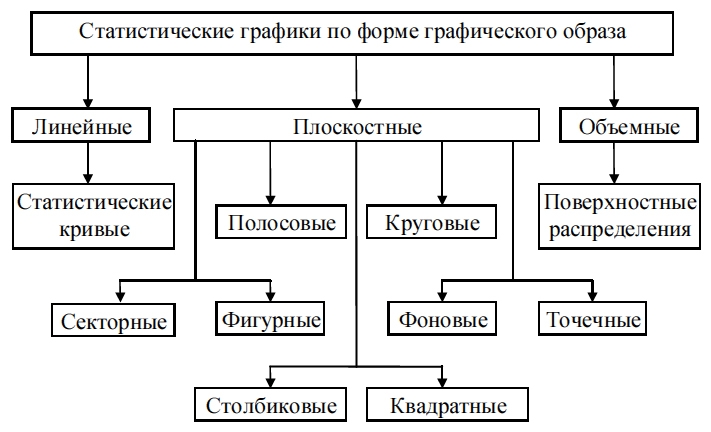
2) По форме применяемых графических образов: точечные, линейные, плоскостные и фигурные;
3) По цели использования: для характеристики структуры, сравнения по территориям и фирмам, оценки динамики и выполнения плана, характеристики вариации, оценки взаимосвязей.
Рис. 5.3. Классификация статистических графиков по форме графического образа
Рис. 5.4. Классификация статистических графиков
по способу построения и задачам изображения
Диаграммы
Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. Диаграмма – наиболее распространенный способ графических изображений. Диаграммы бывают разных видов: линейные, радиальные, точечные, плоскостные, объемные, фигурные. Вид диаграммы зависит от вида представляемых данных и задачи построения графика.
Когда число уровней в ряду динамики велико, целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать, если целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.
Для построения линейных графиков применяют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т.д.), а по оси ординат — размеры изображаемых явлений или процессов (уровни ряда динамики или темпы их изменения). Полученные точки соединяют отрезками в виде ломаной линии. Каждая точка линейной диаграммы соответствует уровню динамического ряда (или темпу его изменения) на определенный момент или за период времени.
На одном графике может быть размещено несколько диаграмм, что позволяет сравнивать динамику различных показателей, либо одного показателя по разным регионам или странам.
На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в графике в связи с тем, что нарушение равновесия между осями координат дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.
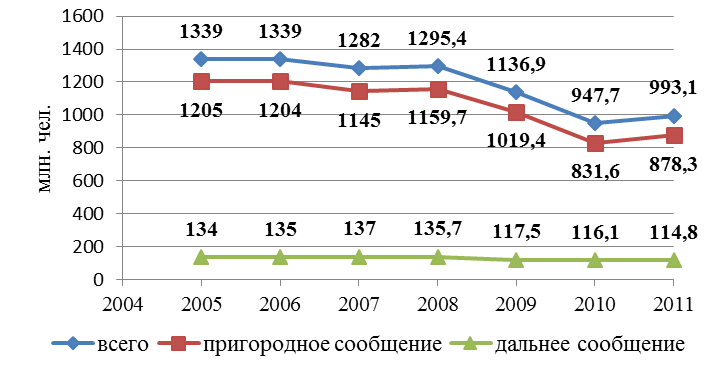
Примеры линейных диаграмм представлены на рис. 5.5 и 5.6.
Рис. 5.6. Динамика пассажирооборота на всех видах транспорта, млрд. пасс.-км
Рис. 5.6. Динамика перевозок пассажиров железнодорожным транспортом, млн. чел.
Для тех же целей, а именно анализа динамики социально-экономических явлений, оценки выполнения плана и характеристики вариации в рядах распределения могут использоваться также столбиковые диаграммы.
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат. При этом каждое значение изучаемого показателя изображается в виде вертикального столбика. По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика. Высота столбиков (в соответствии с принятым по оси ординат масштабом) должна строго соответствовать изображаемым данным.
Количество столбиков определяется числом изучаемых показаний (данных). Столбики могут располагаться вплотную или на одинаковом расстоянии друг от друга. У основания столбиков дается название изучаемого показателя. Уровни (величины), характеризующие значения изображаемых показателей, помещаются внутри каждого столбика.
Столбиковые диаграммы могут использоваться также для пространственных сопоставлений: сравнения по территориям, странам, фирмам, по различным видам продукции. Кроме того, столбиковые диаграммы широко используются для изучения структуры явлений.
Примеры столбиковых диаграмм представлены на рис. 5.7 и 5.8.
Рис. 5.7. Динамика перевозки пассажиров всеми видами транспорта, млн. чел.
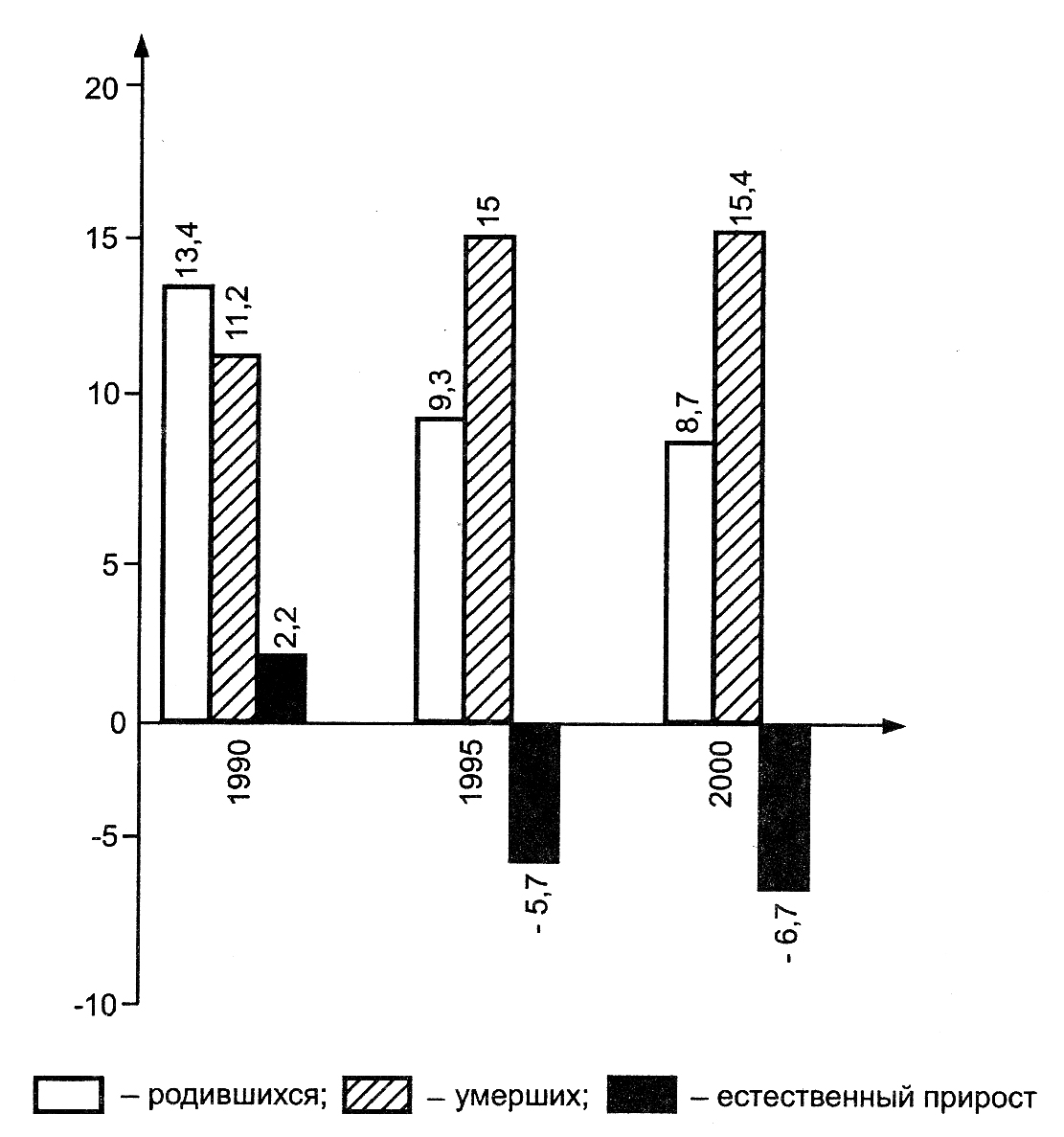
Рис. 5.8. Общие показатели рождаемости, смертности и естественного прироста
населения Российской Федерации, ‰
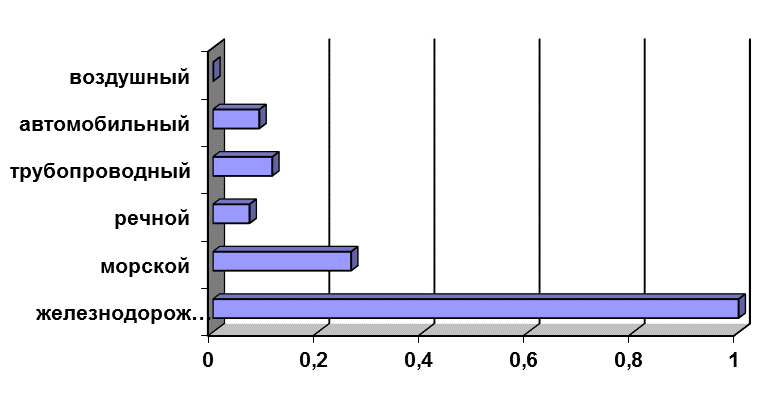
В статистике находят применение и так называемые ленточные (полосовые) графики. По своей форме ленточная диаграмма представляет ряд простирающихся по оси абсцисс полос одинаковой ширины. Длина полос (лент) соответствует значениям изображаемых показателей. При построении ленточных диаграмм соблюдаются те же требования, что и при построении столбиковых графиков (одинаковая ширина полос, начало масштабной шкалы от нулевой отметки и др.). В качестве примера полосовой диаграммы приведем графическое изображение грузооборота различных видов транспорта по отношению к грузообороту железнодорожного транспорта (относительные величины координации) (рис. 5.9).
Рис. 5.9. Соотношение грузооборота различных видов транспорта
по отношению к железнодорожному
Диаграммы, выполненные в виде выдвигающихся от начала масштабной шкалы полос, представляют определенное практическое удобство для систематического отображения хода выполнения производственных заданий нарастающим итогом.
Широкое применение для характеристики структуры социально-экономических явлений нашли секторные диаграммы. В этих диаграммах площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей. При этом поскольку площади секторов пропорциональны их центральным углам, то для построения секторной диаграммы сумма всех углов (360°) распределяется пропорционально удельным весам отдельных частей изучаемой совокупности. При процентном выражении состава изучаемой статистической совокупности исходят из соотношения 1 % = 3,6°.
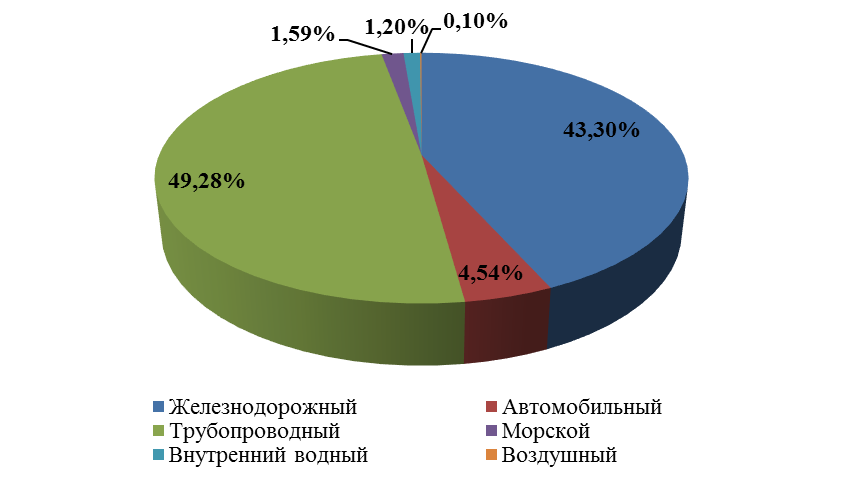
Пример секторной диаграммы представлен на рис. 5.10.
Рис. 5.10. Структура грузооборота различных видов транспорта, 2011 г.
При изучении статистической информации применяются так называемые радиальные диаграммы. Строятся они на базе полярных координат. Началом отсчета в них служит центр окружности, а носителями масштабных шкал являются радиусы круга. Обычно в основе радиальных диаграмм лежат повторяющиеся годовые циклы с помесячными или поквартальными данными. Так, при изучении годового цикла с помесячными данными окружность делят радиусами на 12 равных частей. Каждому радиусу дается название месяца года, а их расположение подобно циферблату часов. На каждом радиусе в соответствии с установленным масштабом наносятся точки, соответствующие изучаемым за каждый месяц данным. Полученные таким образом точки соединяют между собой линиями. В результате получается спиралеобразная линия, характеризующая внутригодовые циклы.
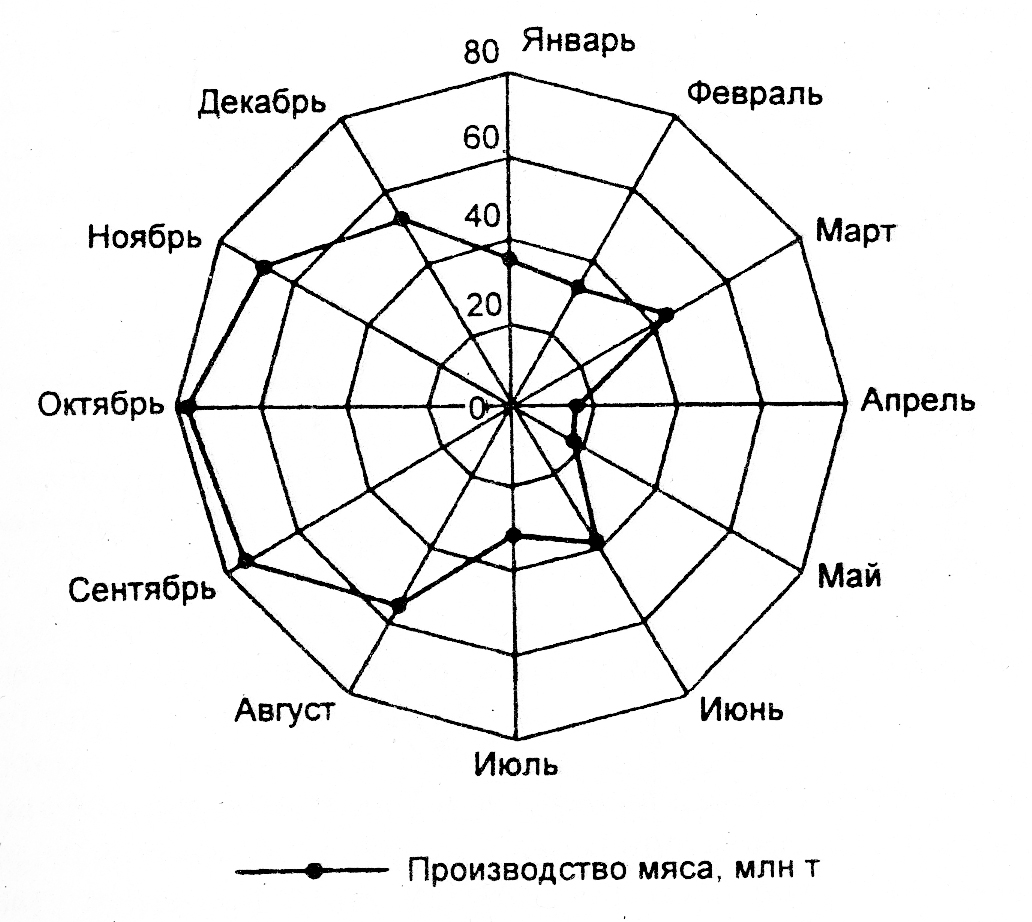
Пример радиальной диаграммы представлен на рис. 5.11.
Рис. 5.11. Производство мяса в регионе N, 2013 г.
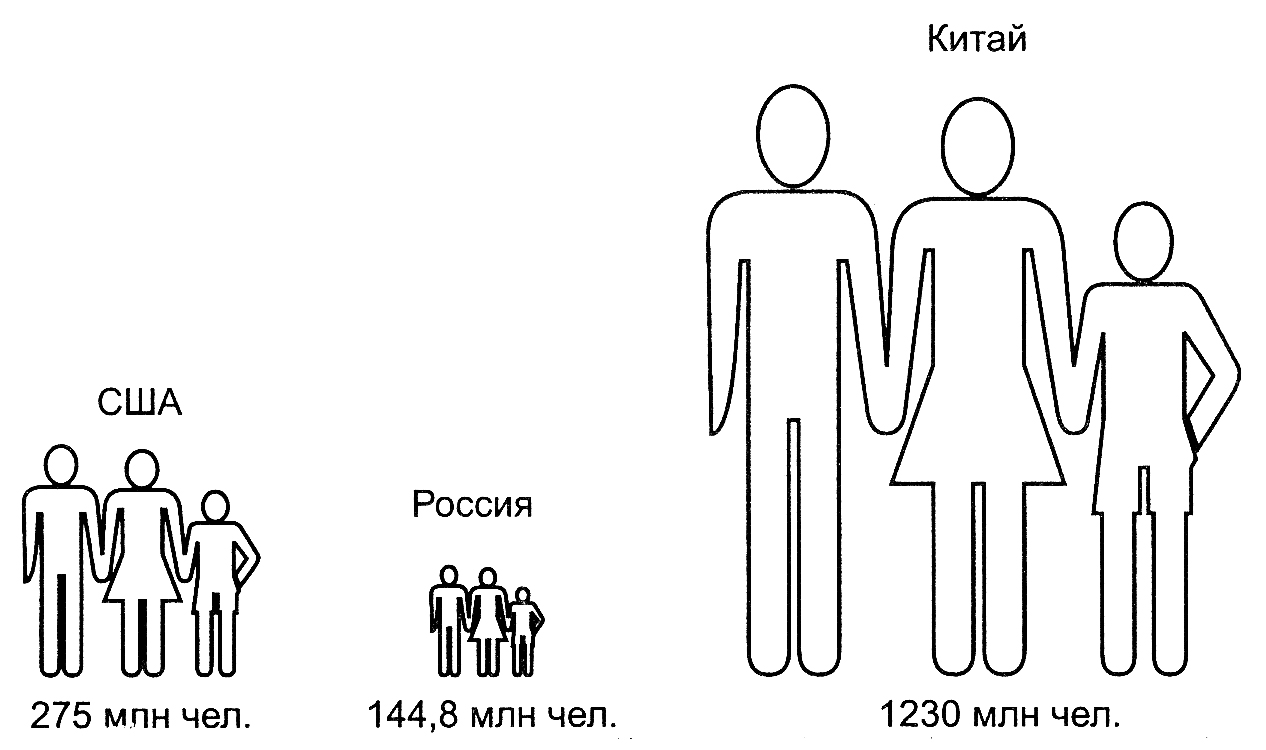
В статистике, прежде всего для рекламных целей, применяются также фигурные диаграммы. При их построении статистические данные изображаются рисунками-символами, которые в наибольшей степени соответствуют существу отображаемых явлений. Эти диаграммы более выразительны, легко воспринимаются зрительно. В фигурных статистических показателях каждому знаку символу условно придается определенное числовое значение, и путем последовательного их расположения на поле графика формируются соответствующие полосы.
Площадь фигуры соответствует величине показателя. Недостатком фигурных диаграмм является то, что графическое изображение изучаемого явления знаками-символами не всегда соответствует точному значению изображаемых данных. Поэтому наряду с целыми фигурами приходится иметь дело с их частями. Это придает отображаемым показателям приближенное значение.
Примеры фигурных диаграмм представлены на рис. 5.12 и 5.13.
Рис. 5.12. Численность постоянного населения на конец 2002 года
Рис. 5.13. Производство мяса в регионе N
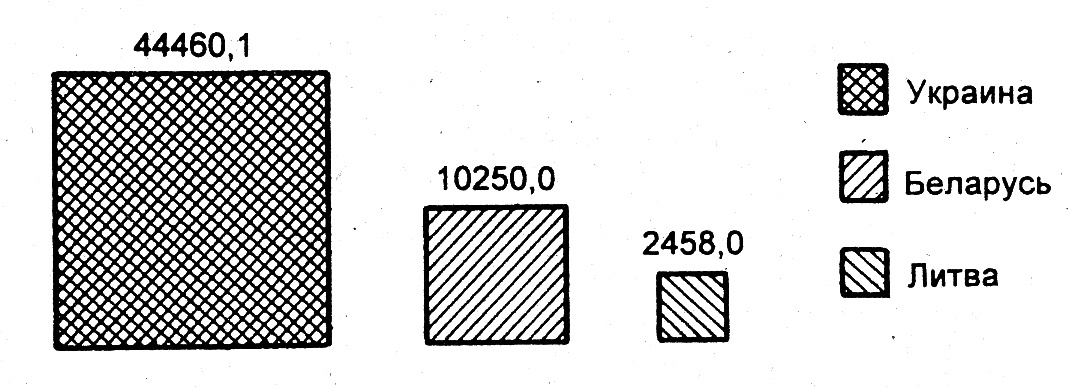
Для простого сравнения независимых друг от друга показателей могут также использоваться круговые, квадратные, прямоугольные диаграммы. Принцип их построения состоит в том, что площади правильных геометрических фигур выражают величины изображаемых явлений.
Примеры квадратных и круговых диаграмм представлены на рис. 5.14 и 5.15.
Рис. 5.14. Квадратная диаграмма поставки российского газа в страны ближнего зарубежья,
январь-август 1995 г.
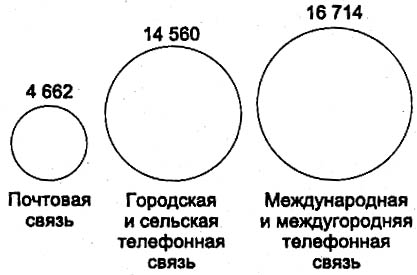
Рис. 5.15. Круговая диаграмма доходов от услуг связи
населению Российской Федерации, 2000 г.
Источник
Статистические графики.
Поможем написать любую работу на аналогичную тему
Графиками в статистике называются условные изображения числовых величин и их соотношений в виде различных геометрических образов – точек, линий, плоских фигур и т.п.
Каждый график состоит из графического образа и вспомогательных элементов.
Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Эти знаки образуют собственно языковую ткань графика, его основу.
Вспомогательными элементами графика являются:
1) поле графика – это пространство, в котором размещаются образующие график геометрические знаки. Поле графика характеризуется его форматом, т.е. размером и пропорциями (соотношением сторон);
2) пространственные ориентиры, определяющие расположение геометрических знаков в поле графика. Пространственные ориентиры задаются системой координат и координатной сеткой, которая делит это поле на части. Чаще применяют систему прямоугольных координат, реже – систему полярных координат.
3) масштабные ориентиры, придающие геометрическим знакам количественную определенность. Масштабные ориентиры определяются системой масштабных шкал или специальными масштабными шкалами.
4) экспликация графика, состоящая из объяснения:
— предмета, изображаемого графиком (его названия);
— смыслового значения каждого знака, применяемого в данном графике.
Без экспликации график нельзя прочитать и понять. Название графика должно точно и кратко раскрывать его содержание. Пояснительные тексты могут располагаться в пределах графического образа или рядом с ним (ярлыки), а также выноситься за его пределы (ключ).
Статистические графики можно классифицировать по различным признакам: назначению (содержанию), способу построения и характеру графического образа.
По содержанию или назначению можно выделить графики сравнения в пространстве, графики различных относительных величин, графики размещения по территории и т.п.
По способу построения графики можно разделить на диаграммы, картограммы и картодиаграммы.
По характеру графического образа различают графики: точечные, линейные, плоскостные (столбиковые, квадратные, круговые, секторные, фигурные) и объемные.
Наибольшее распространение получили диаграммы. Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений. Ниже приведены примеры выполнения некоторых графиков.
Рис. 1. Пример изображения линейного графика
Рис. 2. Пример изображения столбиковой диаграммы
Рис. 3. Пример изображения ленточной диаграммы
Рис. 4. Пример изображения круговой диаграммы
Рис. 5. Пример изображения фигурной диаграммы
Рис. 6. Пример картограммы.
Рис. 7. Пример картодиаграммы
Для изображения вариационных рядов применяются линейные и плоскостные диаграммы построенные в прямоугольной системе координат.
При дискретной вариации признака графиком вариационного ряда служит полигон распределения.
Полигон распределения представляет собой замкнутый многоугольник абсциссами вершин которого являются значения варьирующего признака а ординатами – соответствующие им частоты.
Для построения полигона на оси ординат откладывают в масштабе частоты f а по оси абсцисс – значения признака х. На поле наносят точки с координатами (fi, хi) Затем эти точки соединяют последовательно прямыми отрезками Иногда крайние точки соединяют с осью абсцисс Пример построения полигона приведен на рис. 8, где изображено распределение частот разрядов рабочих по данным табл. 1.
При непрерывной вариации признака используют интервальные вариационные ряды графическим изображением которых служит гистограмма.
Гистограмма представляет собой ступенчатую фигуру, состоящую из прямоугольников, высотой, равной количеству частот в каждом интервале.
Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов. Эти интервалы являются основаниями прямоугольников, площади (высота) которых равны либо пропорциональны частотам распределения в соответствующих интервалах Пример построения гистограммы приведен на рис. 9, где изображено распределение частот разрядов рабочих по данным табл. 3.
Для иллюстрации рядов распределения используются также кумуляты.
Кумулята – это кривая накопленных частот. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумуляты), соответствующих этим значениям признаков. Пример построения кумуляты показан на рис. 10.
Ордината кумулятивного графика показывает, сколько единиц или какая часть совокупности имеет значение признака, не превосходящее указанного на оси абсцисс.
Особый вид статистических графиков представляют собой номограммы, при помощи которых с достаточной для практики точностью получают решение уравнений, вычисляют значения функций нескольких аргументов и т.д. Номограммы удобны для графического изображения и применения уравнений множественной линейной регрессии.
Источник
