Статистика: конспект лекций.
6.4. Способы отбора и виды выборки.
В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.
В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки:
Типическую (стратифицированную, районированную);
Собственно случайная выгборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц.
Случайный порядок подобен жеребьевке. На практике он чаще всего применяется при использовании специальных таблиц случайных чисел. Если, например, из совокупности, содержащей 1587 единиц, следует отобрать 40 единиц, то из таблицы отбирают 40 четырехзначных чисел, которые меньше 1587.
В том случае, когда собственно случайная выборка организуется как повторная, расчет стандартной ошибки производится в соответствии с формулой (6.1). При бесповторном способе отбора формула для расчета стандартной ошибки будет:
Где 1 – n / N – доля единиц генеральной совокупности, не попавших в выборку. Так как эта доля всегда меньше единицы, то ошибка при бесповторном отборе при прочих равных условиях всегда меньше, чем при повторном. Бесповторный отбор организовать легче, чем повторный, и он применяется намного чаще. Однако величину стандартной ошибки при бесповторном отборе можно определять по более простой формуле (5.1). Такая замена возможна, если доля единиц генеральной совокупности, не попавших в выборку, большая и, следовательно, величина близка к единице.
Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности. Довольно часто генеральная совокупность такая большая, что провести подобную предварительную работу чрезвычайно сложно и нецелесообразно, поэтому на практике применяют другие виды выборок, каждая из которых не является строго случайной. Однако организуются они так, чтобы было обеспечено максимальное приближение к условиям случайного отбора.
При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения. Однако практически легче организовать механическую выборку, чем собственно случайную, и при проведении выборочных обследований чаще всего пользуются этим видом выборки. Стандартную ошибку при механической выборке определяют по формуле собственно случайной бесповторной выборки (6.2).
Типическая (районированная, стратифицированная) выборка преследует две цели:
• обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам;
• увеличить точность результатов выборочного обследования.
При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут содержать одинаковое или различное число единиц отбора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке, как с равной, так и неравной долей отбора, удается устранить влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть не от величины общей дисперсии ?2, а от величины средней из групповых дисперсий ?i2. Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки.
При определении стандартных ошибок типической выборки применяются следующие формулы:
• при повторном способе отбора.
• при бесповторном способе отбора:
– средняя из групповых дисперсий в выборочной совокупности.
Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство. Стандартная ошибка серийной выборки определяется по формулам:
• при повторном способе отбора —
Где ?– межсерийная дисперсия выборочной совокупности; r – число отобранных серий;
• при бесповторном способе отбора —
Где R – число серий в генеральной совокупности.
В практике те или иные способы и виды выборок применяются в зависимости от цели и задач выборочных обследований, а также возможностей их организации и проведения. Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированные. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно случайной и т. д. К комбинированной выборке прибегают для обеспечения наибольшей репрезентативности с наименьшими трудовыми и денежными затратами на организацию и проведение обследования.
При комбинированной выборке величина стандартной ошибки выборки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле.
Где ?1 и ?2 – стандартные ошибки соответственно механической и типической выборок.
Особенность многоступенчатой выгборки состоит в том, что выборочная совокупность формируется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного способа и вида отбора отбираются единицы первой ступени. На второй ступени из каждой единицы первой ступени, попавшей в выборку, отбираются единицы второй ступени и т. д. Число ступеней может быть и больше двух. На последней ступени формируется выборочная совокупность, единицы которой подлежат обследованию. Так, например, для выборочного обследования бюджетов домашних хозяйств на первой ступени отбираются территориальные субъекты страны, на второй – районы в отобранных регионах, на третьей – в каждом муниципальном образовании отбираются предприятия или организации и, наконец, на четвертой ступени – в отобранных предприятиях отбираются семьи.
Таким образом, выборочная совокупность формируется на последней ступени. Многоступенчатая выборка более гибкая, чем другие виды, хотя в общем она дает менее точные результаты, чем выборка того же объема, но сформированная в одну ступень. Однако при этом она имеет одно важное преимущество, которое заключается в том, что основу выборки при многоступенчатом отборе нужно строить на каждой из ступеней только для тех единиц, которые попали в выборку, а это очень важно, так как нередко готовой основы выборки нет.
Стандартную ошибку выборки при многоступенчатом отборе при группах разных объемов определяют по формуле.
Где ?1, ?2, ?3, . – стандартные ошибки на разных ступенях;
n1, n2, n3, ... – численность выборок на соответствующих ступенях отбора.
В том случае, если группы неодинаковы по объему, то теоретически этой формулой пользоваться нельзя. Но если общая доля отбора на всех ступенях постоянна, то практически расчет по этой формуле не приведет к искажению величины ошибки.
Сущность многофазной выгборки состоит в том, что на основе первоначально сформированной выборочной совокупности образуют подвыборку, из этой подвыборки – следующую подвыборку и т. д. Первоначальная выборочная совокупность представляет собой первую фазу, подвыборка из нее – вторую и т. д. Многофазную выборку целесообразно применять в случаях, если:
Для изучения различных признаков требуется неодинаковый объем выборки;
Колеблемость изучаемых признаков неодинакова и требуемая точность различна;
В отношении всех единиц первоначальной выборочной совокупности (первая фаза) необходимо собрать менее подробные сведения, а в отношении единиц каждой последующей фазы – более подробные.
Одним из несомненных достоинств многофазной выборки является то обстоятельство, что сведениями, полученными на первой фазе, можно пользоваться как дополнительной информацией на последующих фазах, информацией второй фазы – как дополнительной информацией на следующих фазах и т. д. Такое использование сведений повышает точность результатов выборочного обследования.
При организации многофазной выборки можно применять сочетание различных способов и видов отбора (типическую выборку с механической и т. д.). Многофазный отбор можно сочетать с многоступенчатым. На каждой ступени выборка может быть многофазной.
Стандартная ошибка при многофазной выборке рассчитывается на каждой фазе в отдельности в соответствии с формулами того способа отбора и вида выборки, при помощи которых формировалась ее выборочная совокупность.
Взаимопроникающие выгборки – это две или более независимые выборки из одной и той же генеральной совокупности, образованные одним и тем же способом и видом. К взаимопроникающим выборкам целесообразно прибегать, если необходимо за короткий срок получить предварительные итоги выборочных обследований. Взаимопроникающие выборки эффективны для оценки результатов обследования. Если в независимых выборках результаты одинаковы, то это свидетельствует о надежности данных выборочного обследования. Взаимопроникающие выборки иногда можно применять для проверки работы различных исследователей, поручив каждому из них провести обследование разных выборок.
Стандартная ошибка при взаимопроникающих выборках определяется по той же формуле, что и типическая пропорциональная выборка (5.3). Взаимопроникающие выборки по сравнению с другими видами требуют больших трудовых затрат и денежных расходов, поэтому исследователь должен учитывать это обстоятельство при проектировании выборочного обследования.
Предельные ошибки при различных способах отбора и видах выборки определяются по формуле ? = t?, где ? – соответствующая стандартная ошибка.
Источник
Методы выборки



Выборка в маркетинговом исследовании
Методы выборки
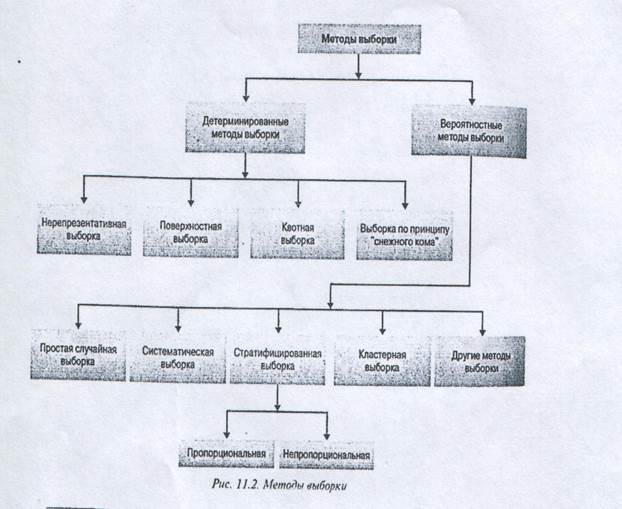
Методы выборочного наблюдения (методы выборки) делятся на две основные категории:
2) вероятностные (рис. 1).
1) Детерминированный метод выборки (nonprobability sampling) — метод выборки, в котором не применяется процедура случайного отбора элементов, в значительной степени основан на индивидуальных предпочтениях исследователя.
Исследователь может произвольно или сознательно решать, какие элементы включать в выборку. В результате проведения детерминированной выборки можно получить детальную оценку характеристик совокупности. Однако этот метод не позволяет объективно оценить точность результатов исследования. Поскольку невозможно определить вероятность включения в выборку каждого отдельного элемента, полученные результаты нельзя статистически распространять на всю совокупность.
Чаше принято использовать следующие детерминированные методы: нерепрезентативная выборка, поверхностная выборка, выборка по квотам и выборка по принципу снежного кома.
Вероятностный метод выборки (nonprobability sampling) — процедура проведения выборочного наблюдения, в соответствии с которой каждый элемент совокупности имеет определенную вероятность включения в выборку.
При использовании вероятностного метода выборки единицы выборки подбираются случайно. Вполне реально предварительно определить все возможные выборки конкретного объема, которые можно получить из генеральной совокупности, а также вероятность получения каждой выборки. Каждая потенциальная выборка не должна иметь одинаковую вероятность получения, но возможно установить вероятность получения любой конкретной выборки определенного размера. Для этого нужно не только точно определить изучаемую совокупность, но и основные характеристики основы выборки.
Так как элементы выбираются произвольно, можно определить точность оценки исследуемых характеристики в каждой выборки. Так как элементы выбираются произвольно, можно определить точность оценки исследуемых характеристик в каждой выборке. Можно рассчитать доверительные интервалы, в пределах которых с определенной достоверностью получают истинные значения характеристик генеральной совокупности. Это позволяет исследователю сделать выводы или высказать предположения относительно изучаемой совокупности, из которой получена выборка.
Классификация вероятностного метода выборки основана на использовании:
— элементарного или кластерного метода отбора;
— одинаковой или различной вероятности отбора единицы выборки;
— целостного или стратифицированного метода отбора;
— случайного или систематического метода отбора;
— одноступенчатой или многоступенчатой технологии.
Группа Детерминированных методов выборки
1) Нерепрезентативная выборка (convenience sampling) — исследователи стремятся создать выборку из удобных, доступных для отбора элементов; отбор элементов для включения в выборку проводится, главным образом, интервьюером. Иногда отбор респондентов для участия в исследовании основан на том, что они оказались в нужном месте и в нужное время.
Пример использования: опрос студентов; опрос членов церковных групп и общественных организаций; опрос покупателей торгового центра без предварительной квалификации респондентов; исследования в универмагах с использованием перечня счетов покупателей; отрывные анкеты в журналах и опрос прохожих на улице.
Преимущества нерепрезентативной выборки:
— наиболее экономная с точки зрения временных и финансовых затрат;
— элементы выборки доступны, готовы сотрудничать;
— их характеристики легко измерить.
Ограничения метода:
— большой риск возникновения различных ошибок выборки, включая самовыбор респондентов;
— этот вид выборки не может представлять какую-либо определенную совокупность, поэтому абсолютно некорректно распространять на генеральную совокупность выводы, полученные при анализе нерепрезентативной выборки;
— не подходит для маркетинговых исследований, предусматривающих написание заключения обо всей генеральной совокупности;
Пример использования: не рекомендуется пользоваться при проведении дескриптивного или причинно-следственного анализа, но этот тип выборки можно применять в поисковых исследованиях, направленных на появление новых идей, понятий или гипотез. Нерепрезентативные выборки можно применять для создания фокус-групп, для предварительных опросов или в экспериментальных исследованиях. Но даже в указанных случаях следует проявлять осторожность в оценке полученных результатов. Тем не менее, этот метод иногда применяют даже в крупных исследованиях.

2) Поверхностная выборка (judge mental sampling) — разновидность нерепрезентативной выборки в соответствии с которой элементы совокупности отбираются на основе суждений исследователя. Исследователь, применив свои знания или проведя анализ, отбирает элементы включения в выборку, поскольку считает, что они представляют изучаемую совокупность или подходят по другим соображениям.
Пример использования: пробные рынки, выбранные для оценки потенциала нового товара; инженеры, покупающие промышленные товары, выбранные для участия в отраслевых маркетинговых исследованиях, поскольку их считают представителями компаний и т.д. Она полезна, если заказчик не требует подробного заключения о результатах исследования данной совокупности. Поверхностная выборка часто используется в маркетинговых исследованиях предприятий торговли. Дальнейшее развитие этого метода предусматривает деление совокупности на квоты.
3) Квотная выборка (quota sampling) — двухэтапная ограниченная поверхностная выборка. Первый этап включает создание контрольных групп, или квот, из элементов совокупности. Для создания этих квот исследователь фиксирует контрольные характеристики, относящиеся к предмету исследования, и определяет их распределение в изучаемой совокупности. Контрольные характеристики, относящиеся к предмету исследования, которыми могут выступать пол, возраст и раса, определяются на основании мнения исследователя. Часто квоты устанавливаются таким образом, что процентное соотношение элементов выборки, обладающих контрольными характеристиками, равно процентному соотношению элементов совокупности, обладающих этими характеристиками. Другими словами, применение квот обеспечивает соответствие структуры выборки структуре генеральной совокупности с учетом исследуемых характеристик. На втором этапе выбор элементов основан на удобстве отбора или мнении исследователя. После создания квот исследователям предоставляется значительная свобода в отборе элементов для включения в выборку. Единственное требование — соответствие отобранных элементов контрольным характеристикам.
Применяя выборку по квотам, исследователь стремится получить представительную выборку при сравнительно низком уровне затрат. Преимущества такой выборки — ее низкая стоимость и удобство выбора элементов для каждой квоты. В последнее время введен более жесткий контроль за действиями интервьюеров и процедурами проведения опроса, что позволяет уменьшить искажения при отборе. Предложены указания по улучшению качества выборок по квотам при проведении интервью в торговых центрах. При определенных условиях применение выборки по квотам дает результаты, похожие на результаты применения обычной вероятностной выборки.
3) Выборка по принципу «снежного кома» (snowballsampling) — случайным образом подбирают начальную группу респондентов; после проведения опроса респондентов просят помочь выявить других кандидатов, входящих в изучаемую совокупность. В дальнейшем отбор респондентов осуществляется из числа кандидатов, указанных первыми респондентами. Данный процесс, когда респонденты, прошедшие опрос, называют следующих кандидатов, в конце концов, приводит к эффекту «снежного кома». Хотя при отборе первых респондентов использовалась случайная выборка, конечная выборка детерминирована. При этом демографические и психологические характеристики названных кандидатов больше похожи на характеристики назвавших их респондентов, чем при случайном выборе опрашиваемых. Главная задача выборки по принципу «снежного кома» — дать оценку необычным для совокупности характеристикам.
Пример: служить люди, получающие какую-либо государственную или социальную помощь, такую как продовольственные талоны, имена которых не подлежат разглашению; отдельные труппы населения, например овдовевшие мужчины в возрасте до 35 лет, а также представители некоторых меньшинств. Выборка по принципу «снежного кома» также применяется в промышленных исследованиях, осуществляемых покупателями и продавцами в поисках взаимовыгодного делового сотрудничества. Основное преимущество этой выборки состоит в том, что она существенно повышает вероятность обнаружения исследуемой характеристики в совокупности. Ей также присуща относительно небольшая дисперсия выборки и невысокий уровень затрат.
Этот метод эффективнее, чем метод случайного выбора. В других случаях предпочтительнее отбор респондентов с использованием вероятностных выборочных методов.
Группа Вероятностных методов выборки
Вероятностные методы выборки отличаются между собой степенью эффективности. Эффективность выборки — это понятие, отражающее компромисс между затратами, связанными с проведением выборки, и ее точностью. Точность выборки — это степень неопределенности, связанная с измеряемой характеристикой. Чем больше точность, тем выше стоимость, а проведение большинства исследований требует соблюдения разумного баланса затрат и результатов. Исследователь должен стремиться разработать максимально эффективный план выборочного наблюдения с учетом выделенного бюджета. Эффективность вероятностного метода выборки можно оценить, сравнив ее с эффективностью простой случайной выборки.
1) Простая случайная выборка (Simple Random Sampling – SRS) — каждый элемент совокупности имеет известную и равную вероятность отбора; каждая возможная выборка данного объема (n) имеет известную и равную вероятность того, что она станет выборочной совокупностью. Это означает, что каждый элемент отбирается независимо друг от друга. Выборка формируется произвольным отбором элементов из основы выборки. Этот метод похож на розыгрыш лотереи, когда таблички с именами участников помещаются в барабан, который встряхивается, и из него произвольным образом извлекают отдельные таблички, в результате объективно определяются имена победителей. При простой случайной выборке исследователь сначала формирует основу выборочного наблюдения, в которой каждому элементу присваивается уникальный идентификационный номер.
Затем генерируются случайные числа, чтобы определить номера элементов, которые будут включены в выборку. Эти случайные числа могут генерироваться компьютерной программой или выбираться из таблицы. Предположим выборочную совокупность, объем которой равен 10, нужно сформировать из основы выборочного наблюдения, содержащей 800 элементов. Поступают таким образом: выбирают три правые цифры в каждом ряду, начиная с первой колонки и первого ряда табл. 1, и двигаются вниз, пока не будет отобрано 10 чисел из 800. Числа, которые находятся за пределами этого диапазона, не включаются. Выборочная совокупность создается из элементов, соответствующих случайно выбранным номерам. Так, в нашем примере будут выбраны элементы: 480,368,130,167,570.562.301,579,475 и 553. Обратите внимание, что последние три цифры ряда 6(921) и 11(918) не включены в выборочную совокупность, поскольку они находятся за пределами установленного диапазона.
Простая случайная выборка имеет очевидные преимущества. Этот метод крайне прост для понимания. Результаты исследования можно распространять на изучаемую совокупность. Большинство подходов к получению статистических выводов предусматривают сбор информации с помощью простой случайной выборки. Однако метод простой случайной выборки имеет как минимум четыре существенных ограничения. Во-первых, часто сложно создать основу выборочного наблюдения, которая позволила бы провести простую случайную выборку. Во-вторых, результатом применения простой случайной выборки может стать большая совокупность, либо совокупность, распределенная по большой географической территории, что значительно увеличивает время и стоимость сбора данных.
В-третьих, результаты применения простой случайной выборки часто характеризуются низкой точностью и большей стандартной ошибкой, чем результаты применения других вероятностных методов. В-четвертых, в результате применения SRS может сформироваться нерепрезентативная выборка. Хотя выборки, полученные простым случайным отбором, в среднем адекватно представляют генеральную совокупность, некоторые из них крайне некорректно представляют изучаемую совокупность. Вероятность этого особенно велика при небольшом объеме выборки. Простая случайная выборка не часто используется в маркетинговых исследованиях. Более популярен метод систематической выборки.
2) Систематическая выборка (systematic sampling) — задают произвольную отправную точку, а затем из основы выборочного наблюдения последовательно выбирают каждый i-й элемент. Интервал выборки i определяется как отношение объема совокупности N к объему выборки n , с округлением результата до ближайшего целого числа. Например, совокупность состоит из 100 тысяч элементов, а желательный объем выборки равен тысяче респондентов. В этом случае интервал выборки 1 равен 100. Выбирается случайное число между 1 и 100. Если, например, это число равно 23, то выборка состоит из элементов 23, 123, 223, 323,423, 523 и т.д.
Общей чертой систематической выборки и простой случайной выборки является то, что каждый элемент генеральной совокупности имеет известную и равную вероятность выбора. Систематическая выборка отличается от SRS тем, что только допустимые выборки объема п, которые можно получить из генеральной совокупности, имеют известную и равную вероятность выбора. Остальные выборки объема п имеют нулевую вероятность выбора.
При систематической выборке исследователь предполагает, что элементы совокупности расположены в определенном порядке. В некоторых случаях принцип сортировки (например, алфавитный перечень в телефонной книге) не имеет отношения к исследуемой характеристике. В других случаях сортировка непосредственно связана с исследуемой характеристикой. Например, имена владельцев кредитных карточек приводятся с учетом суммы их баланса, а названия фирм определенной отрасли располагаются согласно годовому объему их продаж. Если элементы совокупности расположены по принципу, не связанному с исследуемой характеристикой, результаты систематической выборки аналогичны результатам SRS.
С другой стороны, если принцип расположения элементов связан с исследуемой характеристикой, систематический отбор увеличивает репрезентативность выборки. Если фирмы, какой- либо отрасли расположены по принципу увеличения годового объема продаж, систематическая выборка будет включать как мелкие, так и крупные фирмы. Простая случайная выборка в данном случае может быть нерепрезентативной, включая, например, только мелкие фирмы или непропорциональное число мелких фирм. Если расположение элементов выборки носит циклический характер, систематическим методом можно уменьшать представительность выборки.
Систематическая выборка дешевле и проще, чем простая случайная, поскольку случайный отбор осуществляется только один раз. Кроме того, случайные числа не должны соответствовать определенным элементам, как в SRS. Учитывая, что некоторые перечни содержат миллионы элементов, использование этого метода значительно экономит время, что, в свою очередь, способствует снижению затрат, связанных с исследованием. Если совокупность обладает информацией об исследуемой характеристике, систематический отбор дает возможность получить более репрезентативную и достоверную (с. меньшей ошибкой выборки) выборку, чем метод SRS. Еще одно важное преимущество: систематический отбор можно применять, даже не зная структуру основы выборочного наблюдения. Например, можно опросить каждого i-го человека, покидающего универмаг или торговый центр. Поэтому систематический отбор часто применяется при проведении почтовых и телефонных опросов, а также интервью-«перехватов» в торговых центрах.
3) Стратифицированная выборка, или расслоенная, выборка (stratified Sampling) — это процесс, состоящий из двух этапов, в котором совокупность делится на подгруппы (слои, страты, strata). Слои должны взаимно исключать и взаимно дополнять один другого, чтобы каждый элемент совокупности относился к одному и только одному слою, и ни один элемент не был упущен. Далее, из каждого слоя случайным образом выбираются элементы, при этом обычно используется метод простой случайной выборки. Формально, выбор элементов из каждого слоя может осуществляться только с помощью SRS. Однако на практике иногда применяется систематический отбор и другие вероятностные выборочные методы.
Отличие стратифицированной выборки от квотной состоит в том, что элементы в ней выбираются скорее случайно, а не из удобства или на основании мнения исследователя. Главная задача стратифицированной выборки— увеличение точности без увеличения затрат. Переменные, используемые для деления совокупности на слои, называются стратификационными переменными, критерии для их выбора: однородность, неоднородность, взаимосвязанность и стоимость. Элементы, относящиеся к одному слою, должны быть как можно более однородными, а относящиеся к разным слоям — наоборот, как можно более разнородными. Кроме того, стратификационные переменные должны быть тесно связаны с исследуемой характеристикой. Чем больше переменные соответствуют этим критериям, тем эффективнее уменьшение нежелательных отклонений в выборке.
В конце концов, переменные должны снижать стоимость процесса расслоения, будучи простыми, в оценке и применении. Как правило, для стратификации используют такие переменные, как демографические характеристики (как показано на примере квотной выборки), разновидность покупателя (владельцы кредитной карточки или те, кто ее не имеет), величина фирмы или отрасль промышленности. Для стратификации можно использовать несколько переменных, однако больше двух применяют редко, поскольку это непрактично и экономически неоправданно. Несмотря на то, что количество слоев в расслоенной выборке остается предметом спора, опыт показывает, что использовать нужно не больше шести. При использовании больше шести слоев любое повышение точности сводится на нет увеличением стоимости расслоения и отбора.
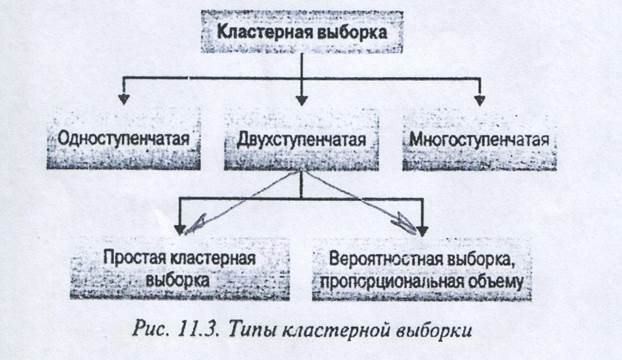
4) Кластерная выборка (cluster sampling) — изучаемая совокупность сначала делится на взаимоисключающие и взаимодополняющие подгруппы, или кластеры (clusters). Затем с помощью вероятностного метода выборки, такого как SRS, формируется случайная выборка кластеров. В выборку включаются либо все элементы отобранного кластера, либо проводится их отбор вероятностным методом. Если в выборку включаются все элементы каждого отобранного кластера, то такая процедура называется одноступенчатой кластерной выборкой. Если выборка получена с помощью вероятностного отбора из каждого выбранного кластера, такая процедура называется двухступенчатой кластерной выборкой. Как показано на рис. 3, существуют два вида двухступенчатой кластерной выборки — простая двухступенчатая кластерная выборка с использованием SRS и вероятностная выборка, пропорциональная объему (PPS). Кроме того, кластерная выборка может состоять из нескольких (больше двух) этапов, выступая как многоступенчатая кластерная выборка.
Основное различие между кластерной и стратифицированной выборкой состоит в том, что в первом случае используются только отобранные подгруппы (кластеры), в то время как в стратифицированной выборке все подгруппы (слои) используются для дальнейшего отбора. Эти методы преследуют разные цели. Цель кластерной выборки — увеличить эффективность выборки, уменьшив затраты на ее проведение. Цель стратифицированной выборки — увеличение точности. По однородности и неоднородности критерии формирования кластеров прямо противоположны критериям формирования слоев. Элементы кластера должны быть максимально разнородны, а сами кластеры — как можно более однородными. В идеале каждый кластер должен представлять собой небольшую модель генеральной совокупности. При кластерной выборке основа выборочного наблюдения необходима только для кластеров, которые вошли в выборку.
Распространенная форма кластерной выборки — территориальная выборка (аrеа sampling), в которой кластеры состоят из географических территорий, таких как округа, жилые районы или кварталы. Если отбор основных элементов проводится в один этап (например, исследователь выбирает некоторые кварталы, а затем все семьи, живущие в этих кварталах, включаются в выборку), такой выборочный метод называется одноступенчатой территориальной выборкой. Если отбор основных элементов проводится в два (или больше) этапа (исследователь выбирает кварталы, а затем в каждом таком квартале отбирает семьи, которые будут включены в выборку), такой метод называется двухступенчатой (или многоступенчатой) территориальной выборкой. Отличительная черта одноступенчатой территориальной выборки заключается в том, что все семьи из выбранных кварталов (или географических регионов) включаются в выборку.
Как показано на рис. 3, существует два типа двухэтапной кластерной выборки. В одном из них метод SRS применяется как на первом этапе (т.е. при выборе кварталов), так и на втором (т.е. при отборе семей в кварталах). Этот метод называется простой двухступенчатой кластерной выборкой. При использовании этого метода количество элементов (семей), отобранных на втором этапе, одинаково для каждого выбранного кластера (отобранного квартала).
Этот метод подходит в том случае, когда все кластеры равны по объему, т.е. каждый кластер содержит примерно одинаковое количество единиц. Однако, если объемы различны, простая двухступенчатая кластерная выборка может привести к ошибочным результатам. Иногда, объединив различные кластеры, можно сделать их равными по объему. Если объединить кластеры нельзя, следует воспользоваться вероятностной выборкой, пропорциональной объему(РРS).
При вероятностной выборке, пропорциональной объему (Probability Proportionate to size Sampling — PPS) кластеры отбираются с вероятностью, пропорциональной их объему. Объем кластера определяется количеством входящих в него единиц выборки. Поэтому на первом этапе большие по объему кластеры имеют большую вероятность включения в выборку. На втором этапе вероятность отбора единицы из выбранного кластера обратно пропорциональна его объему. Поэтому вероятность включения в выборку будет равной для всех выборочных единиц, поскольку неравная вероятность включения на первой стадии отбора компенсируется неравной вероятностью включения на второй стадии.
Кластерная выборка обладают двумя основными преимуществами — выполнимость и низкая себестоимость. Во многих ситуациях единственными легко доступными инструментариями для изучения совокупности будут не элементы, а кластеры. Часто невозможно составить список всех потребителей, входящих в состав определенной совокупности, принимая во внимание ресурсы данного исследования и связанные с ним ограничения.
Однако перечень географических территорий, телефонных кодов определенного района и других кластеров потребителей получить довольно легко. Кластерная выборка наиболее эффективна с точки зрения затрат. Однако, несмотря на это преимущество, ей присущ ряд ограничений. В результате отбора по кластерам создаются относительно неточные выборки. Кроме того, сложно сформировать неоднородные кластеры, так как, например, семьи, живущие в одном квартале, имеют больше схожих признаков, чем различий.
Преимущества и недостатки основных методов формирования выборки
Источник