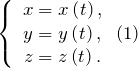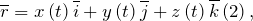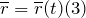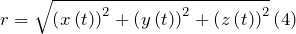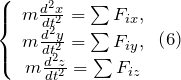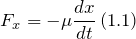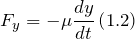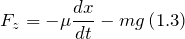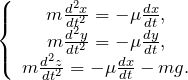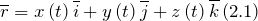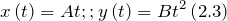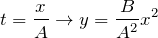iSopromat.ru
Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.
Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.
В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.
Векторный
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
Координатный
При координатном способе задания движения задаются координаты точки как функции времени:
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
Естественный
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
По какому способу определяют закон движения точки
Движение. Виды движений. Описание движения. Система отсчета.
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
А) Равномерное прямолинейное движение материальной точки.
Б) Равноускоренное прямолинейное движение материальной точки.
В) Движение тела по дуге окружности с постоянной по модулю скоростью.
Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.
1. Векторный способ описания движения
ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.
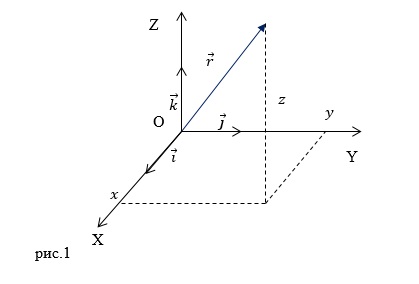
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.
При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.
В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.
2. Координатный способ описания движения
ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.
В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.
Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )
Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: rx = x , ry = y , rz = z .
3. Естественный способ описания движения
ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.
Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.
Источник
Законы движения материальной точки
Кинематические законы движения
Механическим движением называют изменение положения тела относительно тел, составляющих систему отсчета. Для того чтобы описать движение тела следует выбрать систему отсчета в которую ходят: тело отсчёта, система координат, которая связана с телом отсчета и часы (отсчет времени). Движение можно описать при помощи трех способов: координатного (скалярного), векторного, траекторного (натурального).
В декартовой системе координат (рис.1) положение материальной точки (M) определяют три координаты (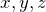
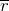
Если точка перемещается, то в любой следующий момент времени координаты изменяются:
Уравнения (1) называют скалярными кинематическими уравнениями движения материальной точки (параметрическими уравнениями). Данные уравнения определяют перемещение точки координатным способом.
Радиус- вектор можно определить как:
где 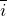
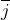
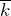
является векторным кинематическим уравнением движения материальной точки. Выражения 1-3 называют кинематическими законами движения материальной точки. Данные законы полностью описывают движение точки.
Модуль (длина) радиус- вектора 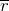
Динамические законы движения материальной точки
Динамика рассматривает движение материальной точки в зависимости от сил, которые к ней приложены. Основные законы классической динамики сформулированы Ньютоном.
Первый закон Ньютона:
Материальная точка не изменяет своего состояния покоя или движется равномерно и прямолинейно, если внешние силы на нее не действуют или действие их взаимно скомпенсированы.
Второй закон Ньютона:
В инерциальных системах отсчета результирующая сил (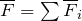
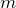
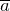
Дифференциальные уравнения движения материальной точки записываю как:
где 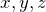
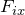
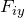
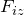
С помощью дифференциальных уравнений перемещения материальной точки при известной массе находят силы, которые действуют на точку.
Примеры решения задач
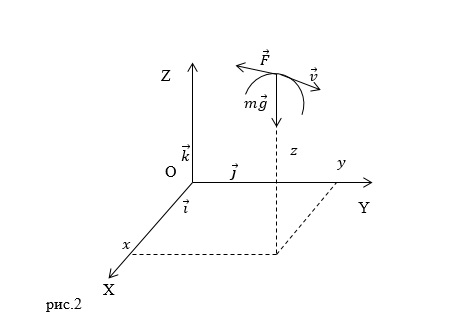
| Задание | На материальную точку действуют сила тяжести (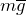 ) и сила сопротивления, пропорциональная скорости ( ) и сила сопротивления, пропорциональная скорости (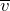 ) движения точки ( ) движения точки (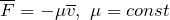 ) (рис.2). Составьте динамические уравнения движения материальной точки. ) (рис.2). Составьте динамические уравнения движения материальной точки. |
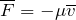 являются выражения:
являются выражения: Применяя второй закон Ньютона выражения (1.1) — (1.3) преобразуем к виду:
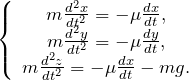
| Задание | Радиус — вектор материальной точки задан функцией: 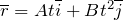 , где , где 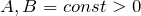 0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»141″ style=»vertical-align: -4px;»/>, 0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»141″ style=»vertical-align: -4px;»/>, 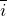 , , 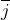 — орты осей X и Y. Запишите уравнение траектории ( — орты осей X и Y. Запишите уравнение траектории (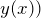 , изобразите ее график. , изобразите ее график. |
| Решение | Векторное кинематическое уравнение имеет вид: |
В условии задачи радиус 0 вектор задан как:
Следовательно, сравнивая выражения (2.1) и (2.2) имеем:
Выразим из первого уравнения (2.3) время и подставим его во второе уравнение, получим:
Уравнение траектории — это парабола (рис.3).
Источник