Плоская система сил сходящиеся силы способы сложения сходящихся сил

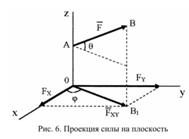
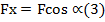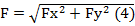Сложение плоской системы сходящихся сил. Силовой многоугольник. Главный вектор.

ПССС- это система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке. ПССС можно сложить геометрическим способом, который называется способом силового многоугольника.

Последовательно вычерчивают векторы сил, заданной системы один за другим и получают ломаную линию, которую необходимо замкнуть. Замыкающий вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу.

Полученный многоугольник АВСDEK называется – силовым многоугольником.

Геометрическая сумма всех сил данной системы называется главным вектором этой системы F_гл.

Замыкающая сторона (АК) полученного силового многоугольника является равнодействующей данной системы сил. Следовательно- равнодействующая ПССС равна главному вектору этой системы сил.

ГЕОМЕТРИЧЕСКОЕ УСЛОВИЕ РАВНОВЕСИЯ:

Система СС уравновешена тогда и только тогда, когда силовой многоугольник замкнут, т.е. равнодействующая равна нулю.

Проекция силы на ось. Правило знаков. Определение силы по ее проекциям.

Проекция силы на ось – взятый со знаком + или – отрезок оси, заключенный между двумя перпендикулярными опущенными из начала и конца силы на ось.

Проекция силы на ось это скалярная алгебраическая величина.

Проекция силы на ось положительная при одинаковом направлении вектора силы и оси и отрицательная при противоположном направлении вектора силы и оси.

Проекция силы на ось это произвольная модуля силы на соS угла между силой и полож. направлением оси.

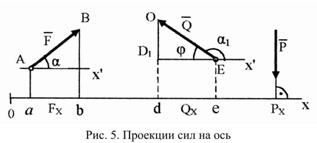
Модуль силы определяется по теореме Пифагора

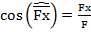
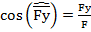
Направление силы F определяется при помощи направляющих косинусов. Это cos угла между вектором силы и положительным направлением оси. (5)

Теорема о проекции геометрической суммы векторов на ось.

Проекция геом. Суммы векторов на какую либо ось равна алгебраической сумме проекций, составляющих сил (векторов) на ту же ось.

Из теоремы следует, что проекция равнодействующей системы сходящихся сил на какую либо ось равна алгебраической сумме проекций, составляющих сил на ту же ось.

Аналитическое определение равнодействующей плоской системы сходящихся сил.

Система сходящихся сил (ССС) – это система, образованная силами, линии действия которых пересекаются в одной точке (рис. 1.1).

ССС эквивалентна одной силе, которая равна геометрической сумме всех сил, входящих в эту систему, и проходит через точку пересечения этих сил. Эта сила называется — равнодействующей данной ССС или главным вектором. Систему сил, изображённую на (рис 1.1), можно заменить эквивалентной системой, где силы F1, F2, F3, F4 перенесены вдоль линии их действия в точку О пересечения этих линий (рис. 1.2). Сложить силы геометрически можно, используя способ построения силового многоугольника (рис. 1.3) или последовательных параллелограммов. При построении силового многоугольника каждый последующий вектор откладывается от конца предыдущего. Вектор силы, соединяющий начало первой отложенной силы с концом последней, является вектором равнодействующей силы R.

Так как данный способ является графическим, то для его реализации необходимо задать масштабный коэффициент F для изображения векторов сил. Длина вектора силы Fi на плане определится по формуле:

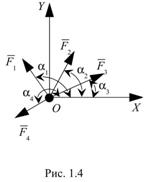
Аналитический способ задания силы. Для задания силы аналитическим способом необходимо выбрать систему координатных осей Охуz, по отношению к которой будет определяться направление силы в пространстве и задать отдельно точку приложения силы А ее координатами x, у, z. Для решения задач механики удобнее задавать силу ее проекциями Fx, Fy, Fz на координатные оси (рис. 6). Зная эти проекции, можно определить модуль силы F и углы α, β, γ, которые она образует с координатными осями Оx, Оу, Оz, по формулам:

Способы сложения и разложения сил.Величину, равную геометрической сумме сил системы, называют главным вектором этой системысил. Это понятие не следует отожествлять с понятием о равнодействующей.

1. Сложение двух сил. Геометрическая сумма R двух сил F1 и F2 , находится по правилу параллелограмма (рис. 7, а) или построением силового треугольника (рис. 7, б). Если угол между силами равен , то модуль R определяется по формулам:

2. Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил (рис..9, а) определяется построением силового многоугольника. Для этого откладываем от произвольной тючки О (рис. 9, б) вектор Oa , изображающий в выбранном масштабе силу F1 , от точки а — вектор ab , изображающий силу F2 , и т. д. Соединяя начало первого вектора с концом последнего, получаем вектор On= R изображающий геометрическую сумму или главный вектор слагаемых сил:

9. Геометрическое и аналитическое условие равнодействующей плоской системы сходящихся сил.

Геометрическое условие равновесия. ССС уравновешена, когда силовой многоугольник замкнут. Чтобы уравновесить ССС, изображенную на (рис. 1.2), надо добавить к ней силу Fур, равную по величине равнодействующей, но противоположную ей по направлению (рис. 1.3). Сила которая уравновешивает данную ССС, называется уравновешивающей.

Аналитическое условие равновесия. Плоская ССС уравновешена, когда суммы проекций всех сил на каждую из двух координатных осей равны нулю:

Для определения равнодействующей плоской ССС можно использовать метод сложения проекции сил на координатные оси:

где ai ─ угол между положительным направлением оси x и направлением силы Fi (рис. 1.4).

Направление равнодействующей R определится направляющим косинусом:

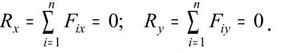
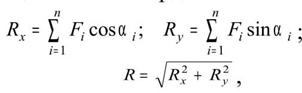
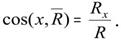
Пара сил. Момент пары сил.

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 12, а). Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Кратчайшее расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к вращательному эффекту и характеризуется моментом пары.

Векторный момент пары сил. Момент пары сил — это вектор М , модуль которого равен произведению модуля одной из сил пары на ее плечо (М = ±Fd) и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Но, в отличие от момента силы вектор m , как будет показано ниже, может быть приложен в любой точке (такой вектор называется свободным).

Момент пары сил относительно точки равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары: M₀(F) = ±F a

Точка О, относительно которой берется момент силы, называется центром момента.

Плечо силы(а) –это перпендикуляр, опущенный из центра момента (точка О) на линию действия сил.

Момент силы относительно точки – является скалярной алгебраической величиной.

Правило знаков такое же, что и для момента силы относительно центра.

Измеряется момент пары, как и момент силы, в ньютон -метрах.

Свойства момента силы относительно точки:

1.Момент силы относительно данной точки не меняется при переносе силы вдоль её линии действия, так как при этом не изменяется ни модуль силы, ни её плечо.

2. Момент силы относительно данной точки равен нулю, если линия действия силы проходит через эту точку, так как в этом случае плечо силы равно нулю: а=0

Свойства пар сил.

1.Теорема 1: алгебраическая сумма моментов сил пары относительно любой точки в плоскости действия этой пары- величина постоянная для данной пары и равна её моменту.

2. Пару сил можно перемещать в плоскости её действия.

3. У данной пары можно произвольно менять модули сил и длину плеча, сохраняя неизменным их произведение, т.е. момент.

4. Теорема2. Эквивалентность пар сил: две пары сил, имеющие равные моменты, эквивалентны, т.е. оказывают на тело одинаковое действие.

Дата добавления: 2018-05-09 ; просмотров: 2989 ; Мы поможем в написании вашей работы!

Источник

Тема1.2. Плоская система сходящихся сил

§1. Геометрический способ сложения сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил

(рис. 1, a), откладываем от произвольной точки О (рис. 1, б) век­тор Oa, изображающий в выбранном масштабе cилу F₁, от точки a откладываем вектор

, изображающий силу F₂, от точки b откла­дываем вектор bc, изображающий силу F₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F_n. Соединяя начало первого вектора с концом последнего, получаем вектор

, изображающий геометрическую сумму или главный вектор слагаемых сил:

От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Рис.1. Система сил

Фигура, построенная на рис. 1,б, называется силовым (в общем случае векторным) многоугольником. Таким обра­зом, геометрическая сумма или главный вектор несколь­ких сил изображается замы­кающей стороной силового многоугольника, построенно­го из этих сил (правило сило­вого многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора

— в сторону противоположную.

Сходящимися называются силы, линии дей­ствия которых пересекаются в одной точке, называемой центром системы (см. рис. 1, а).

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 1, а в точке А).

Последовательно применяя аксиому параллелограмма сил, прихо­дим к выводу, что система сходящихся сил имеет равнодей­ствующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы

сходятся в точке A (рис. 1, а), то сила, равная главному вектору , найденному построением силового мно­гоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

Примечания.

1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник — отличный от первого.

2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.

3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.

§2.Равновесие системы сходящихся сил

Из законов меха­ники следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инер­ции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода:

1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».

2) Уравно­вешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравнове­шенных сил.

Для равновесия приложенной к твердому телу системы сходя­щихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовле­творять сами силы, можно выразить в геометрической или аналити­ческой форме.

1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то

Источник