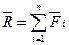Плоская система сходящихся сил определение равнодействующей силы графическим способом

wiki.eduVdom.com

Инструменты пользователя

Инструменты сайта

Боковая панель

Теория вероятностей и математическая статистика
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
economics

Теоретическая механика. Статика:

Контакты

Графическое определение равнодействующей сходящихся сил

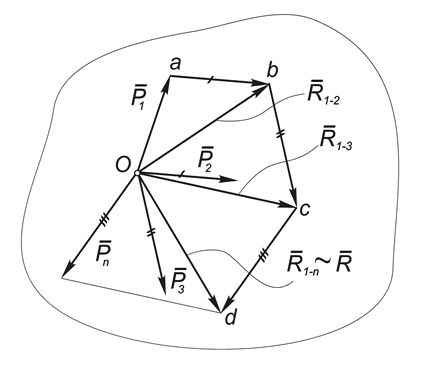
Теорема 1. Равнодействующая системы сходящихся сил существует, приложена в центре системы, равна их геометрической (векторной) сумме и изображается замыкающей стороной силового многоугольника.

Для доказательства рассмотрим систему сходящихся сил, приложенных в центре О : (Рис.1).

По аксиоме параллелограмма две первых силы этой системы можно заменить равнодействующей $\vec>$, которая изображается замыкающей стороной силового треугольника Oab и как вектор равна сумме векторов $\vec<Р_1>$ и $\vec<Р_2>$:

Затем точно так же можно найти равнодействующую силы $\vec>$ и силы $\vec<Р_3>$, откладывая от точки b вектор $bc = \vec<Р_3>$:

Продолжая эту процедуру, мы найдем равнодействующую всей системы:

, которая изображается замыкающей стороной силового многоугольника Oabcd.

Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.

Универсальным для определения равнодействующей системы сходящихся сил является аналитический метод, к рассмотрению которого мы и переходим.

Источник

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

• 1. Аксиомы и понятие силы статики
• 2. Связи и реакции связей
• 3. Определение равнодействующей геометрическим способом
• 4. Определение равнодействующей аналитическим способом
• 5. Пара сил. Момент силы

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n — число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

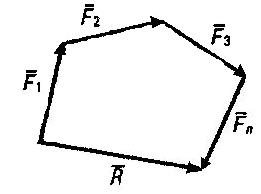
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

Источник

Графический способ определения равнодействующей сходящихся сил на плоскости.

Пусть задана произвольная система сходящихся сил 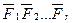, приложенных к твердому телу.

Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействую­щую этих сил. Равнодействующая такой системы может быть определена графически и аналитически.

Графически сложение двух сходящихся сил производится по правилу параллелограмма, причем . Затем по правилу параллелограмма складываем силы и , и получаем их равнодействующую . Продолжая процесс, получим

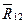
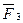
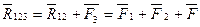
Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил. В силовом мно­гоугольнике конец одной из сил служит началом другой. Равнодействующая сила 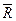в силовом многоугольнике соединяет начало первой силы с концом последней, т.е. изображается замыкающей силового многоугольника.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской — плоской.

Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпадать с началом первой силы.

Такой силовой многоугольник называют замкнутым.

Получено условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равнялась нулю 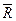= 0. Это условие является геометрическим.

Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.

Источник

Плоская система сходящихся сил

Содержание:

Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Плоская система сходящихся сил — основные понятия и определения

Если все силы, приложенные к телу, расположенные в одной плоскости и линии их действия пересекаются в одной точке, то такая система сил носит название плоской системы сходящихся сил.

Покажем на рис. 1.6 произвольное тело, к которому приложена плоская системы сходящихся сил , , . . При этом линии действия всех сил пересекаются в точке A.

Определение равнодействующей системы сходящихся сил

Геометрический способ сложения сил:

Добавить систему сил означает определить их равнодействующую. Попробуем найти равнодействующую для плоской системы сходящихся сил, которая изображена на
рис. 1.6. Возьмем (условно) две первые силы и и на основании III аксиомы
статики найдем их равнодействующую , для чего на силах и , как на
сторонах, построим свой параллелограмм, диагональ которого, которая приложена в
точке A, и является их равнодействующей . Далее геометрически добавим две следующие силы и , и уже на этих силах как на сторонах построим свой
параллелограмм, диагональ которого будет второй равнодействующей . Так же дальше продолжаем до последней силы . Когда построено последний параллелограмм и проведена последняя диагональ, то она и будет равнодействующей системы сходящихся сил, которая показана на рис. 1.6

Если внимательно присмотреться к геометрическому построению параллелограммов, то можно увидеть, что к концу вектора силы был присоединен вектор силы (то есть в конец вектора перенесено параллельно вектор ) и так далее до последней силы .

Таким образом, геометрический способ добавления сходящихся сил сводится к построению силового многоугольника. Он строится путем параллельного переноса векторов сил в масштабе, когда начало следующей силы совпадает с концом предыдущей силы. Тогда вектор равнодействующей соединяет начало первой силы с концом последней силы. Это можно записать так:

Величина равнодействующей силы не изменится, если будет изменен порядок
присоединения (добавление) сил до многоугольника, но конфигурация силового
многоугольника будет другой.

Условие равновесия плоской системы сходящихся сил в геометрической форме

Если к свободному материальному телу приложена одна сила, то о равновесии этого тела речи не может быть. Таким образом, если рассматривать плоскую систему сходящихся сил, которая сведена к равнодействующей, то тело не может быть в равновесии.

Для равновесия тела под действием плоской системы сходящихся сил необходимо и
достаточно, чтобы равнодействующая всех сил была равна нулю.

Равнодействующая такой системы сил будет равна нулю, когда силовой многоугольник будет замкнутым, то есть когда начало вектора первой силы будет совпадать с концом вектора последней силы.

Теорема о равновесии тела под действием трех не параллельных сил

Если тело под действием системы трех плоских не параллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.

Представим тело (рис. 1.7), к которому в точках А, B, C приложены силы
, , , векторы которых расположены в одной плоскости. Рассмотрим сначала две силы и . На основании следствия из I и II аксиом статики указанные силы всегда можно перенести по линии их действия в одну точку, например, в точку О.

Далее, если есть в точке О две приложенные силы, то на основании III аксиомы статики их можно заменить одной силой, то есть равнодействующей . Построим на рис. 1.7 на указанных векторах сил и параллелограмм и покажем равнодействующую .Теперь тело находится под действием только двух сил и и оно будет в равновесии только тогда, когда векторы этих сил расположены на одной прямой, то есть на прямой CO. Тогда и вектор силы пересекает точку О. Теорема доказана.

Проекция силы на ось и на плоскость

Представим силу , вектор который произвольно расположен в плоскости чертежа (рис. 1.8). Выберем в этой плоскости ось, например, ось x. Необходимо спроектировать указанную силу на эту ось x.

Обозначим сначала конце вектора силы буквами А и В и опустим из них на ось x перпендикуляры. Точки пересечения перпендикуляров с осью x (обозначим их соответствующими строчными буквами а и в) образовали на оси x направленный отрезок, который и будет проекцией силы на ось x. По величине этот отрезок равен произведению модуля силы || на косинус угла, под которым вектор силы пересекает ось. А именно:

По знаку проекция силы на ось тогда будет положительная, когда угол α (угол пересечения направления вектора силы или линии действия силы с осью) острый. В полной мере разумеется, если этот угол равен в 90º, то проекция силы на ось x равна нулю. Если угол α будет тупой, то проекция силы на ось x будет иметь отрицательный знак. Значения проекции в данном случае будет

Но практически тут удобнее использовать тупой угол α₂, а острый угол β между вектором силы и направлением оси x. Знак проекции легко определяется из схемы

Таким образом, проекция силы на ось — это направленный отрезок на оси, образованный между перпендикулярами, которые опущены из концов вектора силы на ось, и который по величине равен произведению модуля силы на косинус угла между направлением вектора силы и осью.

Спроектируем теперь вектор силы на плоскость и оси координат.

Возьмем силу , вектор которой произвольно расположен в пространстве (рис. 1.9). Выберем в пространстве прямоугольную декартову систему координат Oxyz, начало отсчета которой (точка O) совмещенное с точкой приложения вектора силы . Спроектируем вектор силы на плоскость xOy. Опустим из точки А (конец вектора силы) на указанную плоскость перпендикуляр, который пересекает ее в точке а. На плоскости xOy создан вектор , который и является проекцией силы на плоскость. По модулю эта проекция равна

где α — угол между вектором силы и плоскостью xOy.

Следует заметить, что проекция вектора силы на плоскость является вектором, потому что плоскость на имеет базисных векторов, ортов.

Если в плоскости xOy обозначить угол β, то есть возможность спроектировать силу на оси x и y, опуская с точки a на оси перпендикуляры и по известному уже правилу получить проекции вектора на указанные оси:

В данном случае через ось z и вектор силы можно провести плоскость, поэтому есть возможность спроектировать силу на эту ось по известному правилу. Эта проекция будет равняться

где ϒ — угол между вектором силы и осью z.

Определение силы за ее проекциями

Предположим, что у нас в плоскости рисунка имеем прямоугольную декартову систему координат Oxy, заданные две проекции силы — и (рис. 1.10). Надо по данным проекциями вычислить модуль вектора самой силы , а также его направление.

На заданных проекциях, как на сторонах, строим прямоугольник, диагональ которого, проходит через точку пересечения проекций, и является искомым вектором силы . Модуль силы можно определить из следующего выражения:

Углы между вектором силы и осями x и y можно определить с помощью направляющих косинусов

Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.

Аналогично для пространственной системы сил (рис. 1.9) можно построить на проекциях сила как на сторонах параллелепипед, а модуль силы определить так:

Направление вектора этой силы также определяется через направляющие косинусы его углов с соответствующими осями координат x, y и z:

Через арккосинус определяют сами углы.

Теорема о проекции равнодействующей силы на ось

Проекция вектора равнодействующей силы на ось равна алгебраической сумме проекций векторов составляющих сил на ту же ось.

Доказательство. Имеем систему сил , , , ,которая сведена к равнодействующей с помощью силового многоугольника (рис. 1.11). Введем на плоскости прямоугольную декартову систему координат Ox y и спроектируем на ось x все силы. Для этого обозначим концы векторов всех сил буквами — А, В, С, D, K и проведем перпендикуляры из каждой точки на ось x. Точки пересечения перпендикуляров с осью, которые обозначены соответствующими строчными буквами — а, в, с, d, k образовали на оси x направлены отрезки, которые и являются проекциями всех сил на эту ось. Каждая проекция, соответственно, равна

Добавим алгебраически все проекции и подсчитаем, почему эта сумма равна:

Но отрезок ak и является проекцией равнодействующей силы на ось x. Распространяя эту сумму на n сил, можно записать:

Аналитический способ добавления системы сходящихся сил

На основании теоремы о проекции равнодействующей силы на ось, имеем:

Аналогично проекция равнодействующей силы на ось y будет равняться

Модуль равнодействующей равен

Углы между вектором равнодействующей и осями координат x и y определим через направляющие косинусы углов между соответствующей осью и равнодействующей:

Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.

Условия равновесия тела под действием плоской системы сходящихся сил в аналитической форме

Плоскую систему сходящихся сил можно заменить одной силой, которая носит название равнодействующей.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю. А если равнодействующая равна нулю, то и ее проекции на оси x и y тоже должны равняться нулю. Поскольку проекции
равнодействующей равны алгебраическим суммам проекций составляющих сил, то,
окончательно, иметь условия равновесия тела под действием плоской системы
сходящихся сил

Для равновесия тела, находящегося под действием плоской системы сходящихся
сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси
координат были равны нулю.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник