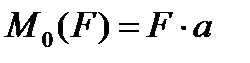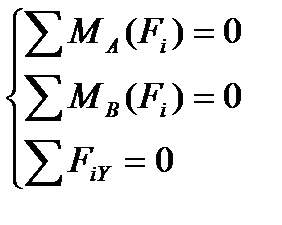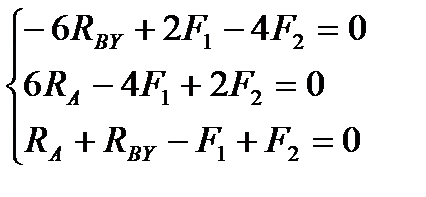Теоретическая механика:
Плоская система сходящихся сил

Смотрите также решения задач по теме «Плоская система сил» в онлайн решебниках Яблонского и Мещерского.

§ 5. Сложение двух сил

Сложение двух сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке, производится по тем же двум правилам – правилу параллелограмма и правилу треугольника, рассмотренным в главе I (§ 1), и теми же методами – графическим, графо-аналитическим и аналитическим (методом проекций).

При сложении сил необходимо учитывать следующее обстоятельство.

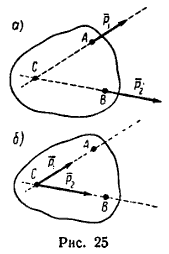
В теоретической механике – в механике твердого тела, сила – скользящий вектор, т. е. при решении задач силу можно переносить вдоль линии ее действия в любую точку. Поэтому, если на тело действуют две силы P₁ и P₂, лежащие в одной плоскости, как, например, показано на рис. 25, а, то эти силы можно перенести в точку C – точку пересечения линий действия данных сил и считать их приложенными таким образом к одной точке тела (рис. 25, б), как это и сделано в задаче 20.

§ 6. Разложение силы на две составляющие

Решение многих практических задач по статике сводится к разложению силы на две составляющие. Подобные задачи, как показано в § 2, решаются либо по правилу параллелограмма, либо по правилу треугольника и, в зависимости от исходных данных, приводятся к одному из четырех типов.

Общая методика решения приведенных ниже задач сводится к следующему:

1. Выбираем метод решения – графический или графо-аналитический.

2. Выбираем правило, по которому будем решать задачу, т. е. либо правило параллелограмма, либо правило треугольника.

3. Если выбран графический метод, то далее выбираем масштаб построения, строим параллелограмм или треугольник (в соответствии с выбранным правилом) и, наконец, измеряем стороны получившейся фигуры, находим модули соответствующих сил, а измерив углы, найдем их направления.

4. Если выбран графо-аналитический метод, то в зависимости от избранного правила строим параллелограмм или треугольник, соблюдая приблизительные соотношения размеров длин и углов, а затем, в зависимости от исходных данных, используем геометрические или тригонометрические соотношения.

§ 7. Многоугольник сил. Определение равнодействующей сходящихся сил

Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом (задача 3), либо методом проекций (задача 18).

Задачи, приведенные в этом параграфе, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.

Порядок решения задач методом проекций изложен в § 4, п. 7.

§ 8. Равновесие сходящихся сил

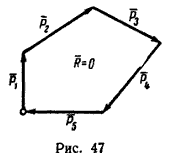
При определении равнодействующей системы пяти сил в задаче 36 установлено, что R=0 и, следовательно, система сил уравновешена. Если из сил, данных в задаче 36, построить векторный (силовой) многоугольник (рис. 47), то увидим, что он замкнется. В этом и состоит геометрическое условие равновесия системы сходящихся сил:
P₁ + P₂ + P₃ + . + P_i = 0.

Из геометрического условия следует аналитическое условие равновесия, выражающееся двумя уравнениями:
∑ X_i = 0 и ∑ Y_i = 0.

Следует заметить, что все задачи, приведенные в § 6, можно решить с применением условия равновесия системы сходящихся сил. Причем при решении задач на равновесие системы сходящихся сил можно использовать те же три метода: графический, графо-аналитический и аналитический (метод проекций).

Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости задачи с плоской системой сходящихся сил):
а) неизвестна одна сила, т. е. ее модуль и направление;
б) неизвестны направления двух сил данной системы;
в) неизвестны модуль одной из сил и направление второй;
г) неизвестны модули двух сил.

При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.

Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутый треугольник, который затем решается на основе геометрических либо тригонометрических соотношений.

Метод проекций целесообразно применять для решения задач с числом сил больше трех.

При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться такой общей для всех систем схемы:

1) выделить тело или точку, равновесие которых рассматривается в данной задаче, и изобразить их на рисунке;

2) выяснить, какие нагрузки действуют на тело (точку) и также изобразить их на рисунке;

3) освободить выделенное тело (точку) от связей и заменить их действие реакциями, которые надо изобразить на том же рисунке;

4) на основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия; причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке);

5) после решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом.

§ 9. Равновесие трех непараллельных сил

При решении задач определенное практическое значение имеет теорема о равновесии трех непараллельных сил: если три непараллельные силы образуют уравновешенную систему, то линии их действия пересекаются в одной точке.

Эта теорема используется для решения задач в тех случаях, когда на тело действует уравновешенная система трех сил, причем одна сила задана по модулю и направлению, для другой известно лишь направление, а у третьей – неизвестны ни модуль, ни направление.

Источник

Методика решения задач плоской системы сходящихся сил

1. Число неизвестных в данных задачах не превышает двух.

2. Рассматриваем точку, находящуюся в равновесии.

3. Определяем наличие активных сил.

4. Освобождаемся от связей и заменяем их реакциями.

5. Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.

6. Решаем уравнения равновесия относительно неизвестных.

7. Выполняем проверку.

Пример.Груз, силой тяжести F1=10Н удерживается в равновесии с помощью связей –гладких поверхностей . Определить реакции связи аналитически и графически.

Решение.

I. Аналитическое решение

1. Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.

2. Выбираем систему координат хОу и составляем таблицу, уравнения равновесия.

силы	=0	=0
R1
R2
F1

3. Составляем систему уравнения и решаем.

Проверка: + =4,7·0,5 +8,46 ·0,9- 10=0

II. Графическое решение.

1. Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F₁.

2. Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R₁+R₂+F₁=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R₁ и R₂ до их пересечения.

3. Определяем реакции связей R₁ и R₂ , умножая полученные результате графического построения отрезки на масштаб.

4. Проверка: Заключается в сравнении значений векторов R₁ и R₂ , найденных аналитическим и графическим способами. r1 = (R_1а — R_1б)/ R_1а; r1 = (R_2а — R_2б)/ R_2а;

Задания для выполнения работы

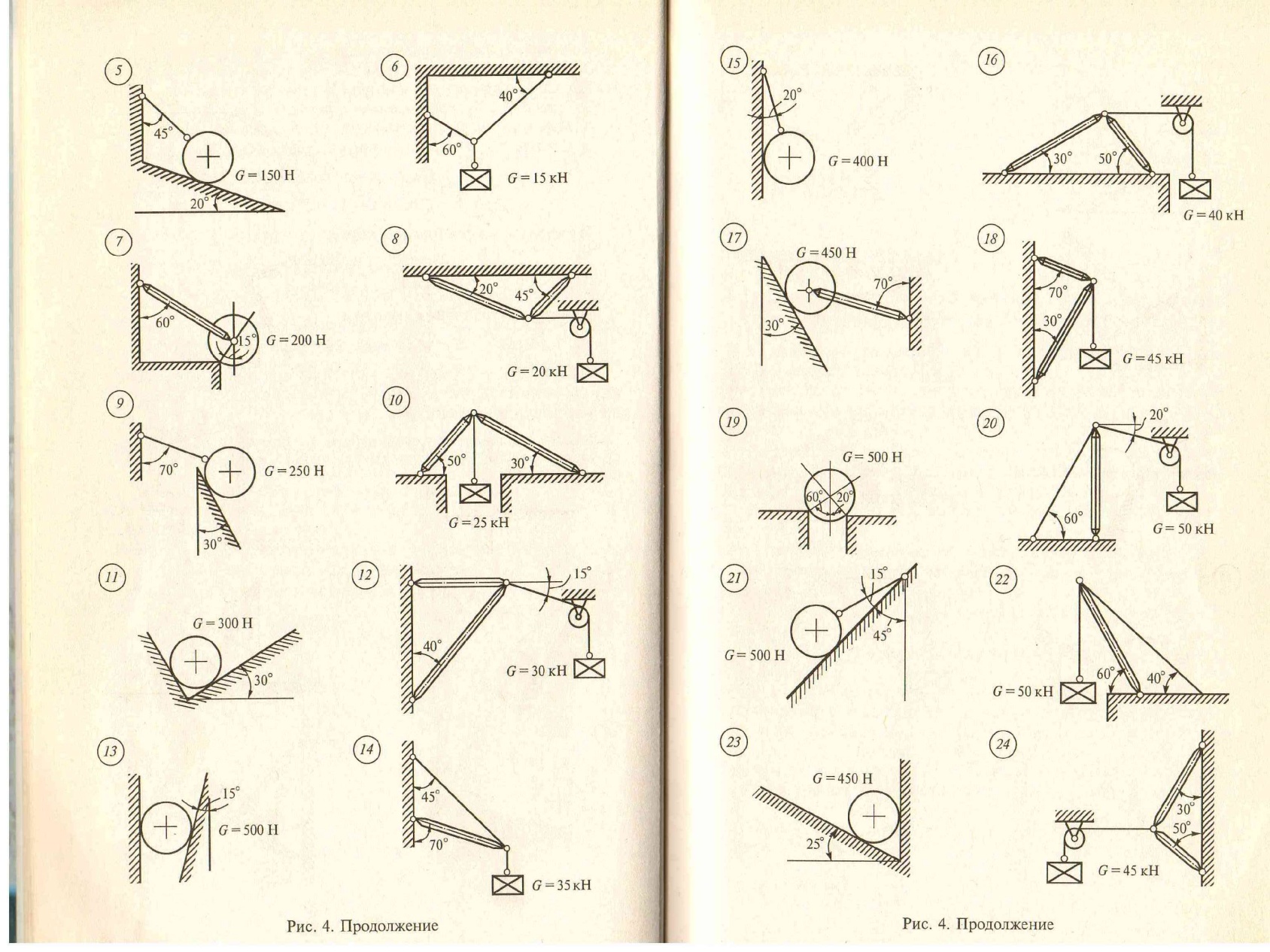
Груз, силой тяжести G удерживается в равновесии с помощью связей. Определить реакции связей, удерживающих груз аналитически и графически.

Контрольные вопросы:

1. В чем отличие между осью и проекцией?

2. Сколько уравнений равновесия Вы составляли при решении задачи?

3. Методика решения задач ПССС.

4. Дайте определение плоской системе сходящихся сил.

5. Какой величиной является проекция силы на координатную плоскость?

Литература:

1. Вереин Л.И. Техническая механика – М: Академия, 2006.

2. Мовнин М.С. Основы технической механики – СПБ: Политехника, 2003.

3. Молчанова Е.В., Шурыгина Г.Н. Статика и сопротивление материалов — Томск, 2008.

Практическая работа №3

Тема урока: Определение реакций в опорах с вертикальными нагрузками

Тип урока:закрепление полученных знаний.

Цель урока:Научиться определять реакции в опорах с вертикальными нагрузками

Обеспечивающие средства:

1. методическое руководство по выполнению работы;

3.тетрадь для практических работ;

4.карандаш, линейка, ластик, авторучка;

Технология работы:

1.Внимательно изучите методические указания, предложенный теоретический материал.

2.В соответствие с вариантом, выполнить задание по методике представленной ниже.

3.Сделайте выводы о проделанной работе.

4.Ответить на контрольные вопросы.

Теоретический материал

Плоская система произвольно-расположенных сил – это система, в которой все силы лежат в одной плоскости, но линии их действия не пресекаются в одной точке.

Момент силы относительно точки

Момент –способность силы создавать вращение (М).

Мо (F) = F * а

Единица измерения М [ Н * м] 1кНм = 10 3 Нм, 1мНм = 10 6 Нм

Момент силы относительно точки равен произведению силы на перпендикуляр, опущенный из точки вращения на линию действия силы.

а – плечо, перпендикуляр или кратчайшее расстояние между точкой вращения и линией действия силы.

Если вращение тела происходит по часовой стрелке, то момент положительный.

Момент отрицательный, если вращение тела против часовой стрелки.

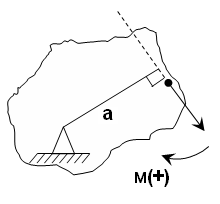
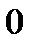
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку вращения, т.к. плеча равно нулю, нет вращения.

Пример. Для двух опорной балки, нагруженной силами F₁, F₂ , определить реакции в опорах R_А и R_В. Силами тяжести балки АВ пренебречь. Опора А шарнирно-подвижная, опора В шарнирно-неподвижная.

Решение.

1. Определяем связи, заменяем их реакциями.

2. Определяем оси координат Х, У.

3. Составляем таблицу уравнения равновесия.

R_BX =0 т.к. все силы располагаются параллельно балке R_B =R_BY

Силы	=0	=0	=0
RА	6RA	RA
RBY	-6RBY	RBY
F1	2F1	-4F1	-F1
F2	-4F2	2F2	F2

4. Составляем уравнение по II-ому виду

Из 1-го уравнения находим R_BY

Из 2-го уравнения находим R_A

5. Проверка: по 3-му уравнению 4,7+1,3-8+2=0

Источник