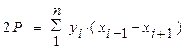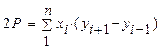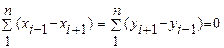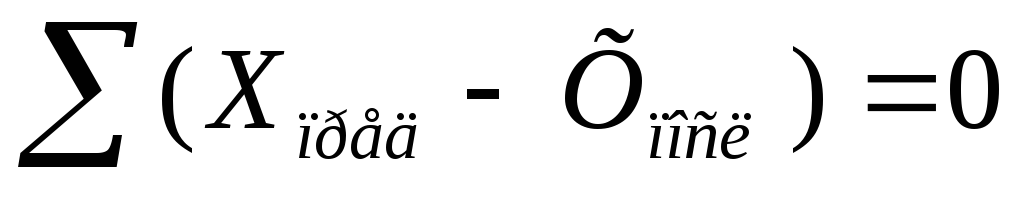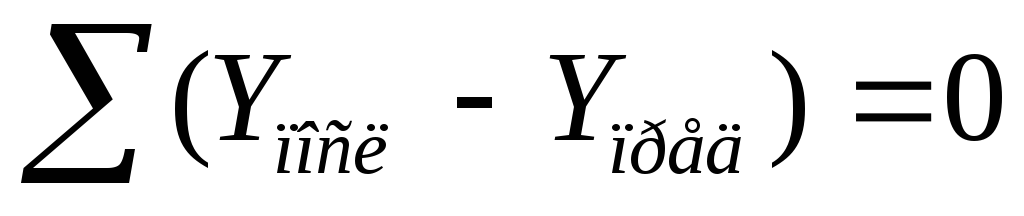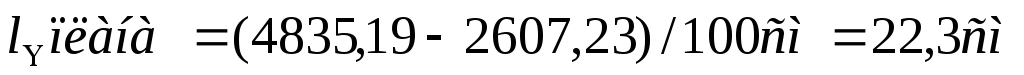Определение площади полигона



Для определения площади строительных участков применяют следующие способы: графический, аналитический, механический.
В выполняемой работе использовать аналитический способ.
Площадь полигона можно вычислить по координатам его вершин. Исходными данными являются координаты точек (вершин) теодолитного хода (полигона).
Рис. 3.4.1 — Схема проекций точек теодолитного хода на координатные оси
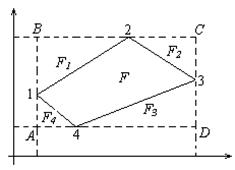
Рис. 3.4.2 — Схема определения площади полигона аналитическим способом
— замкнутый полигон 1-2-3-4-1, (1-2-3-4-5-6-1);
Определить: площадь F полигона.
 , , | (3.4.1) |
где 

Подставим значение площадей в исходную формулу, раскроем скобки и после приведения подобных членов получим:
 . . | (3.4.2) |
Вынесем за скобки одноименные значения:
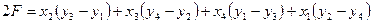 . . | (3.4.3) |
То есть удвоенная площадь полигона равна сумме произведений (для каждой точки полигона) абсциссы х на разность между ординатами у последующей и предыдущей точек.
Данный полигон состоит из четырех точек, поэтому в формуле получилось четыре таких слагаемых. Для полигона из n точек формула примет вид:
 . . | (3.4.4) |
Формулу 7.5 следует читать так: двойная площадь полигона (многоугольника) равна сумме произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек.
Формула для вычисления площади полигона: в формуле (7.4) за скобки можно вынести у:
 , , | (3.4.5) |
После преобразования формула будет иметь вид:
 . . | (3.4.6) |
Формулу 7.7 следует читать так: двойная площадь полигона (многоугольника) равна сумме произведений ординаты каждой точки на разность абсцисс предыдущей и последующей точек теодолитного хода.
Вопросы для контроля:
1. Какой порядок камеральных работ при построении плана теодолитной съемки?
2. Перечислите способы съемки ситуации.
3. По какой формуле вычисляют площадь полигона, контроль?
4. Как контролируют правильность нанесения точек теодолитного хода?
5. Какой размер пересечения координатных линий, каким цветом рисуют?
Источник
Аналитический способ определения площадей



В этом способе площади земельных участков вычисляются по результатам измерений углов и линий непосредственно на местности или по их функциям (координаты, приращения координат).
Наиболее распространенным алгоритмом вычисления площадей земельных участков аналитическим способом является алгоритм вычисления площадей по координатам вершин.
Площади земельных участков аналитическим способом вычисляются по формулам:
Контроль правильности вычисления площадей (только для замкнутого полигона):
Аналитический способ вычисления площадей по непосредственно измеренным величинам на местности или их функциям является наиболее точным, т.к. здесь отсутствуют ошибки графических построений, присущие графическим методам определения площадей участков по планам или картам.
Данным способом посчитана как площадь всего землепользования (см. ПРИЛОЖЕНИЕ А), так и трех севооборотов (см. ПРИЛОЖЕНИЕ В)
Источник
2 Определение площади полигона аналитическим способом
По координатам вершин полигона вычисляется площадь участка по формулам:


Пример вычисления площади полигона представлен в таблице 6. Часто эта таблица является продолжением ведомости вычисления координат.
Произведения в ведомости округляем до 1 м, т.к. это практически не влияет на результат.
Сумма разностей абсцисс и сумма разностей ординат должна равняться 0.
Таблица 6 – Вычисление площади полигона по координатам его вершин
Произведения, м 2
S = 3518936 м 2 = 351,89 га
3 Составление плана по координатам вершин полигона
По данным теодолитной съемки составить план в масштабе 1:10 000.
1) Построение координатной сетки
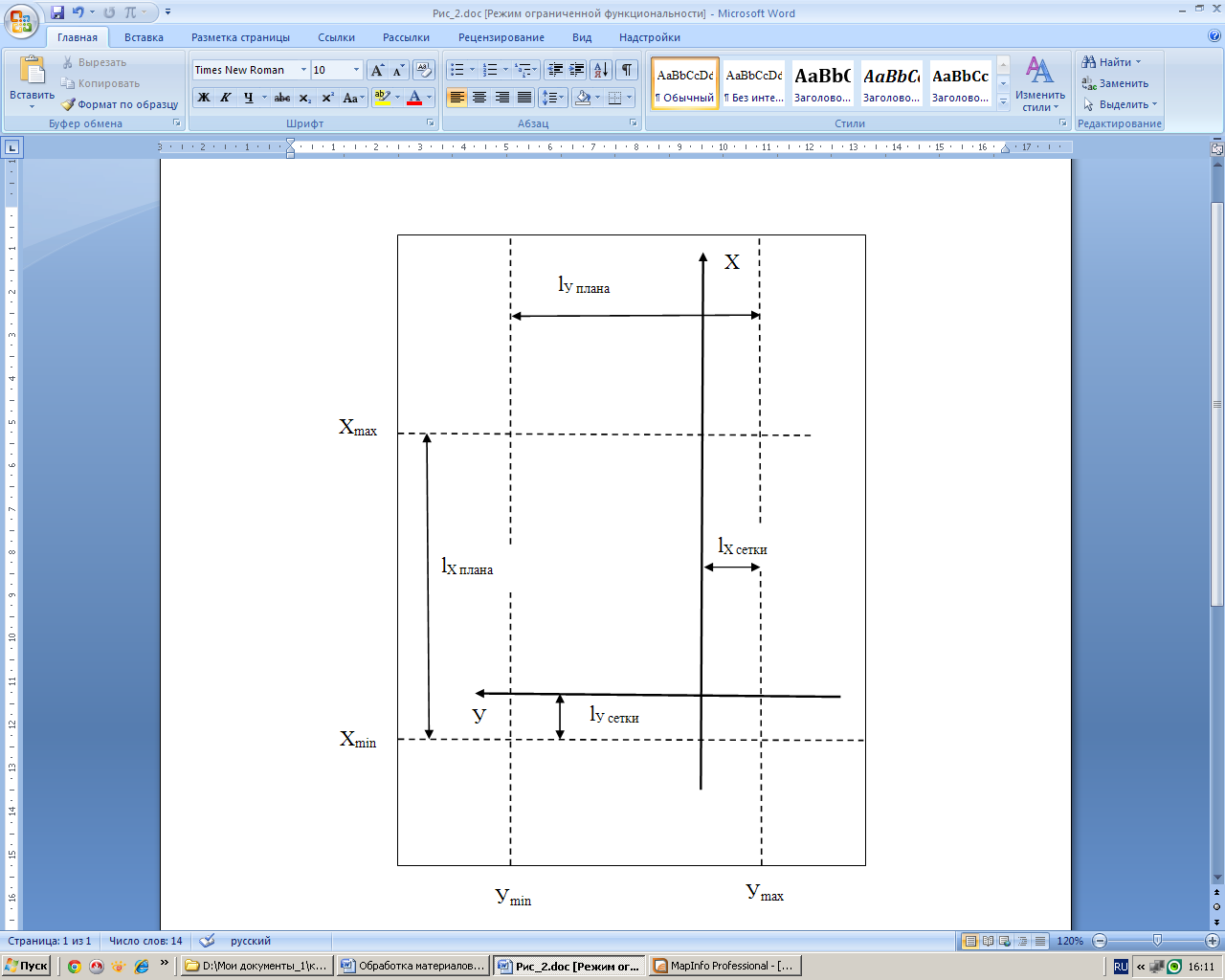
На 1/2 листа чертежной бумаги (формат А-2) построить прямоугольную координатную сетку со сторонами квадратов 10 см так, чтобы полигон разместился симметрично относительно краев листа бумаги (рисунок 2).
Для этого необходимо определить размеры плана полигона с севера на юг и с запада на восток по формулам:
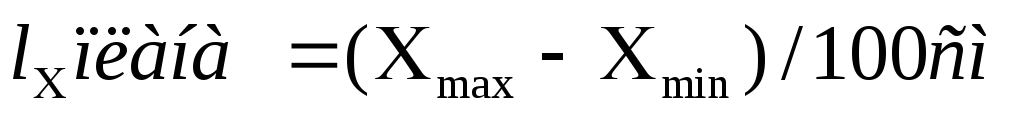
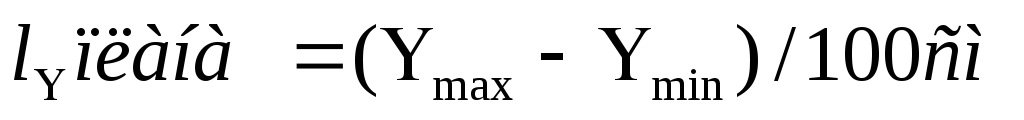
где 100 — число метров местности, соответствующее 1 см на плане согласно масштабу.
В нашем примере размер плана с севера на юг будет
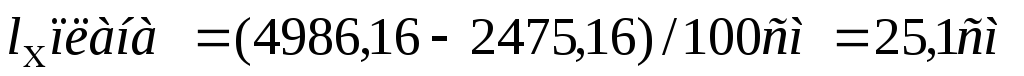
Размер плана с запада на восток будет
Границы полигона намечаются на бумаге таким образом, чтобы сверху остался запас в два раза больше, чем снизу, т.е. снизу отложить
а слева и справа — поровну
(1у листа – 1У плана)/2 (см).
Для листа формата А-2 эти расстояния будут равны:
от нижнего края листа (42 – 25,1) / 3 = 5,6 см;
от левого края листа (59,5 – 22,3) / 2 = 18,6 см.
Далее определяют места ближайших линий координатной сетки относительно нижней и левой границ полигона, соответствующие круглым значениям координат (кратных 1000 м).
Определяют расстояние от нижней границы до ближайшей линии ординат:
и расстояние от левой границы до ближайшей линии абсцисс:
В нашем примере эти расстояния будут равны
lYсетки = (3000 – 2475,16) / 100 = 5,2 см
1Х сетки = (4835,19 – 4000) / 100 = 8,4 см.
Отложив на бумаге эти расстояния, в пересечении найдем положение точки для начала построения координатной сетки.
Рисунок 2 – Расчеты для размещения плана симметрично относительно краев листа
Координатную сетку строят при помощи масштабной линейки и измерителя по способу засечек, известному из геометрии. Контроль правильности построения сетки координат осуществляется путем измерения сторон и диагоналей квадратов, при сравнении которых допускаются расхождения в пределах 0,2мм.
Сетка вычерчивается остро отточенным карандашом по ребру выверенной линейки, а затем закрепляется зеленой тушью тонкими линиями. Подписывают линии координатной сетки со значениями координат, кратными 1000м.
2) Накладка теодолитного хода на план
Все точки полигона и диагонального хода последовательно наносятся на бумагу по координатам с помощью масштабной линейки и измерителя. Нанесение на план точек теодолитного хода производится по их вычисленным координатам.
Для этого сначала определяют квадрат сетки, в котором находиться пункт. Далее на противоположных сторонах этого квадрата циркулем с использованием поперечного масштаба откладывают отрезки, соответствующие разностям одноименных координат точки и «младших» сторон квадрата. Точки отложения отрезков на сторонах квадрата попарно соединяют линиями, пересечение которых дает положение наносимого на план пункта.
Контроль правильности нанесения точек по координатам осуществляется путем сравнения сторон на плане с соответствующими длинами горизонтальных проложений, записанными в ведомости координат. Расхождения не должны превышать 0,2 мм.
3) Нанесение ситуации
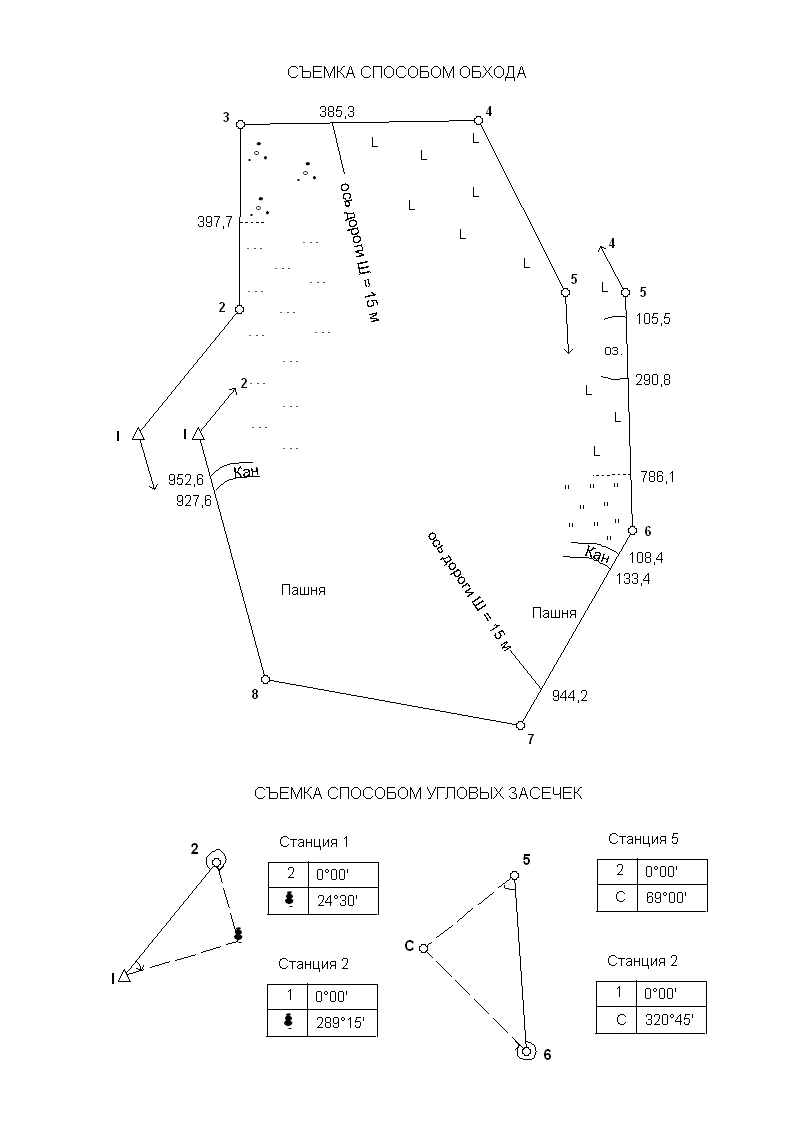
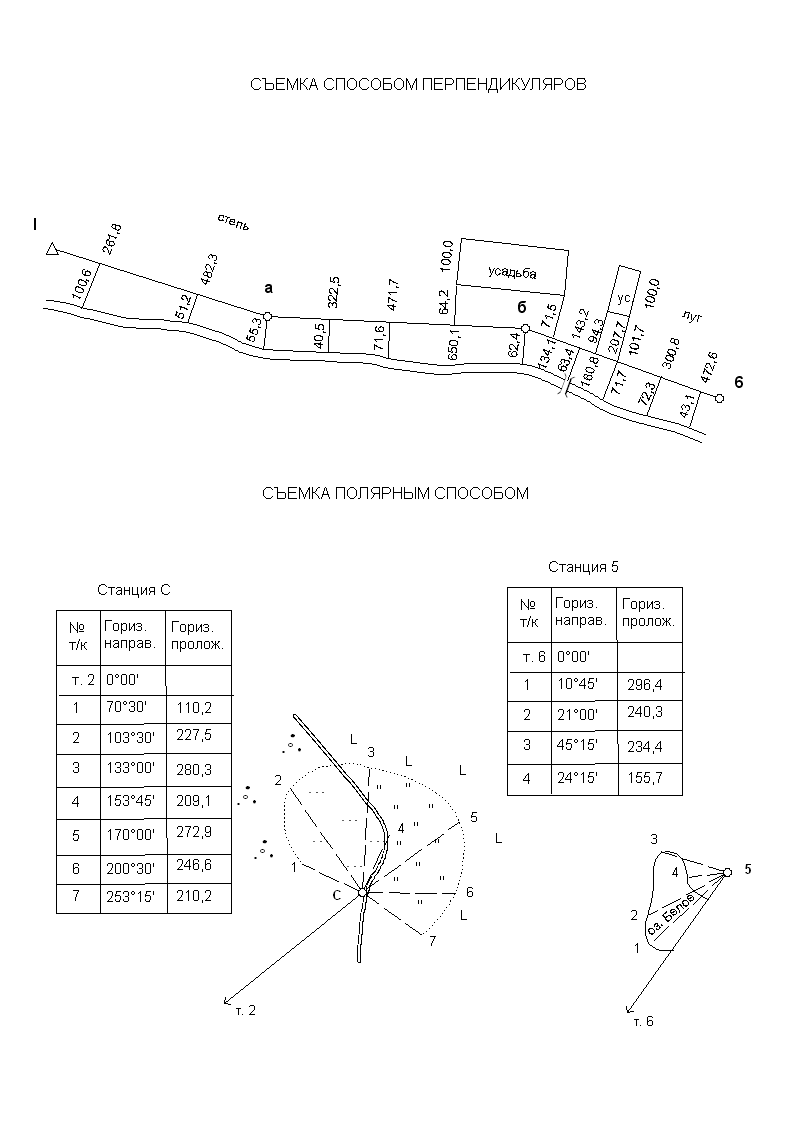
Нанесение контуров на план каждый студент выполняет, руководствуясь абрисом (рис. 3а, 3б).
Способ построения контуров на плане соответствует способу съемки их на местности. Для построения контуров можно пользоваться транспортиром и линейкой с миллиметровыми делениями. Построенные разными способами точки контуров соединить плавными линиями.
Рисунок 3 а – Абрисы съемок
Рисунок 3 б – Абрисы съемок
4) Оформление плана
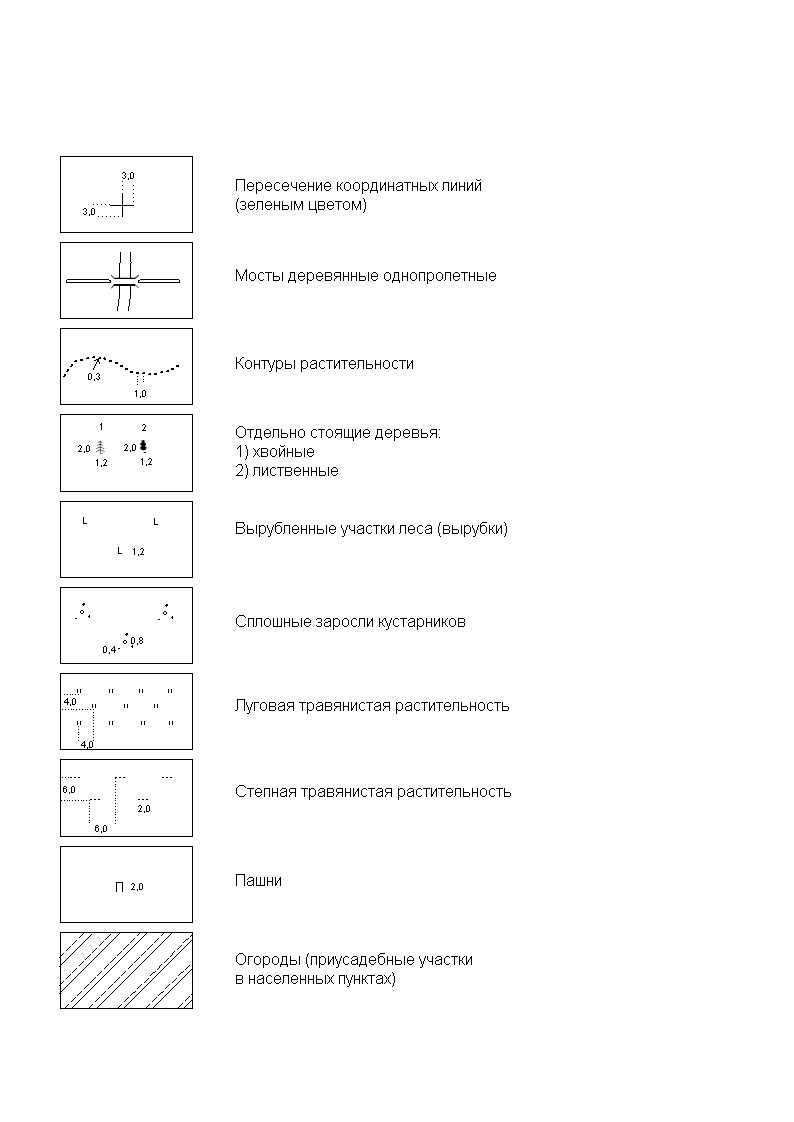
На план нанести условные знаки с соблюдением их размеров и начертаний, согласно «Условным знакам для планов масштаба 1:10000» (рисунок 4). Все линии на плане вычертить толщиной 0,15 мм. Координатную сетку подписать с двух сторон, снизу и слева по осям Х и У.
Напротив линий полигона в виде дроби подписывают дирекционные углы (или румбы) в числителе и длины линий – в знаменателе. Черта дроби должна быть параллельна оси Y, и находится на расстоянии примерно 1 см от линии (рисунок 5).
В верхней части листа крупным шрифтом подписывают «План землепользования», указывают название землепользователя (например, колхоз или АО «Новый путь» Емельяновского района Красноярского края).
Под названием помещают таблицу с указанием площадей угодий, называемую экспликацией (состав угодий).
Внизу под планом указывают масштаб, указывают фамилию составителя плана.
Рисунок 4 – Условные знаки для карты масштаба 1:10000
Источник
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Аналитический способ
При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.
Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.
Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.
Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)
Выразим площадь каждой трапеции через ее основания и высоту:
Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:
или в общем виде:
В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).
Если при группировке членов выносить за скобки Y1, то получится формула:
Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.
Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.
Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.
Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.
На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.
Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:
Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,
Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:
Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:
mP=an * mt * L, (6.17)
где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин; 
его значения:
n 3 4 5 6 7 8 9 10
an 0.204 0.250 0.256 0.250 0.243 0.231 0.222 0.212
n 11 12 15 20 24 30 60 120
an 0.205 0.197 0.179 0.156 0.143 0.128 0.091 0.065
Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.
При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).
Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.
Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.
При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.
Площадь правильного n-угольника можно выразить через его периметр:
И из формулы (6.17) получить формулу относительной ошибки площади:
для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.
Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:
ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.
Источник