Планетарный механизм графический способ

Планетарный механизм графический способ

5.2.2 Планетарный механизм со смешанным зацеплением

(с одним внешним и одним внутренним зацеплением).

Входное звено – первое звено;

Выходное звено – водило.

1– солнечное колесо;

2,3 – блок сателлитов;

4 – коронная шестерня;

Выберем на выходном звене (на водиле ) точку F так, чтобы O₁A=O₂F (O₁ и O₂ соосны ).

1. Графический способ определения передаточного отношения

Отрезок АА’ берем произвольно.

2. Аналитический способ определения передаточного отношения.

Обратим мысленно планетарный механизм в механизм с неподвижным водилом , для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

если (1) переписать через количество зубьев, то

5.2.3 Механизм с двумя внешними зацеплениями.

u (4) _1–Н = 20 ч 50 при η = 0.99

Входное звено – водило;

Выходное – первое колесо.

Например, если u (4) _Н–1= 20, то u (4) _1–Н = 1 /20

Выберем точку F на входном звене так, чтобы O₁F = O₂B.

Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.

ψ₁ и φ₂ – направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.

Применим метод обращения движения.

Запишем передаточное отношение через число зубьев:

5.2.4 Планетарный механизм с двумя внешними зацеплениями.

Применяется в приборных устройствах, так как u (4) _Н–1 до 10 000.

Недостаток – низкий К.П.Д

Выберем на водиле Н точку F так, чтобы O₂F=O₁A (валы O₁ и O₂ соосны ). Точка С может быть выше или ниже точки А.

FF’ – произвольный отрезок (линейная скорость точки F).

Для колес 2 и 3 точка С – МЦС.

5.3 Синтез (проектирование) планетарных механизмов.

Под синтезом в этом курсе будем понимать подбор (определение) чисел зубьев планетарных механизмов при условии, что зубчатые колеса нулевые, а радиальный габарит механизма минимальный.

Расчет на прочность не проводим, но он обязательно должен быть проведен при проектировании.

При проектировании конструктор обязан выполнить ряд условий:

1. Отклонение от заданного передаточного отношения не должно превышать 10% (5%).

2. Обеспечить отсутствие подреза у нулевых зубчатых колес:

У колес с внешними зубьями z₁, z₂, z₃ ≥18 ;

У колес с внутренними зубьями z ≥85.

Если колеса не нулевые, то z_min от 7 для колес с внешними зубьями или z_min от 56 для колес с внутренними зубьями.

3. Обеспечить отсутствие заклинивания в зацеплении сателлит – коронная шестерня.

Заклинивания нет, если z _кш – z_сат ≥ 8

4. Обеспечить выполнение условия соосности входного и выходного звеньев.

5. Необходимо обеспечить выполнение условие соседства (окружности вершин соседних сателлитов не должны касаться друг друга).

6. Обеспечить выполнение условия сборки. Определить условие сборки, исходя из чертежа невозможно, необходимо проверить выполнение этого условия по уравнению ( см . далее).

5.3.1 Проектирование однорядного планетарного механизма.

k = 3 – количество сателлитов

при минимальном радиальном габарите;

Зададимся числом зубьев z₁ так, чтобы выполнялось условие 2, тогда z₁ = 18, z₃ = 5 . 18 = 90 ≥ 85.

Источник

Планетарный механизм графический способ

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

• однорядный планетарный механизм;
• двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
• двухрядный планетарный механизм с двумя внешними зацеплениями;
• двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется «солнечным»;
• колесо с внутренними зубьями называют «короной» или «эпициклом»;
• колеса, оси которых подвижны, называют «сателлитами»;
• подвижное звено, на котором установлены сателлиты, называют «водилом» . Звено водила принято обозначать не цифрой, а латинской буквой h.

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Источник

2.4. Графический метод кинематического анализа зубчатых механизмов

Графический метод применяют для определения линейных скоростей любой точки любого звена механизма, угловых скоростей его звеньев и передаточного отношения механизма.

Линейную скорость точки звена, совершающего вращательное движение, определяют:

(14)

где ω – угловая скорость вращения звена относительно мгно­венного центра вращения;

R – расстояние точки до мгновенного центра вращения.

Из выражения (14) можно заключить, что при ω=const скорости точек меняются по линейному закону, для построения которого необходимо знать скорости только двух точек.

2.4.1. ПЛАНЕТАРНЫЕ МЕХАНИЗМЫ

ПОСТРОИТЬ планы линейных и угловых скоростей звеньев (рис.6)

Дано: ω – угловая скорость колеса 1;

Ζ_1,2,3,4 – числа зубьев всех колес и их модуль (m).

Закон изменения скоростей точек 1-го колеса От линии y — y (вправо или влево) откладывают отрезок про­извольной длины (), считая, что этим отрезком изобразится скорость точки А колеса 1 в определенном масштабе. Так как скорость центра колеса 1 равна нулю (мгновенный центр скоростей), то , соединив точки а и 0 , получают на плане скоростей прямую 1, которая и является законом изменения линейных скоростей точек первого колеса.

Для точек 2 и 3 колес

Скольжение между начальными окружностями зубчатых колес отсутствует, поэтому V_A1 =V_A2. Колеса 2 и 3 находятся на одном валу, следовательно, их угловые скорости равны (ω₂ = ω₃) и закон изменения линейных скоростей их точек, должен быть один. Для его построения необходимо знать скорость еще одной точки этих звеньев. Такой точкой является С: колесо 4 остановлено (ω₄ = 0), поэтому V_С4 = V_С3 = 0 и мгновенным центром скоростей колес 2 и 3 будет точка с. Прямая ас и будет законом изменения линейных скоростей точек колес 2 и 3.

Рис.6.Схема и планы скоростей планетарного механизма

Для точек водила Н

Точка В принадлежит одновременно сателлитам 2, 3 и водилу Н, следовательно, её скорость можно найти, спроектировав В на линию ас – получают точку в. Мгновенным центром вращения водила является его ось, поэтому известны скорости двух точек водила – в и 0 . Прямая в0 – закон изменения скоростей точек водила.

Полученное графическое изображение изменения скоростей точек звеньев зубчатого механизма называют ПЛАНОМ ЛИНЕЙНЫХ СКОРОСТЕЙ

Масштаб плана линейных скоростей

(15)

По этому плану можно определить скорость любой точки звена механизма. Например, для нахождения скорости точки Д необходимо спроектировать эту точку на линию ас (точка Д принадлежит сателлитам 2, 3). Отрезок 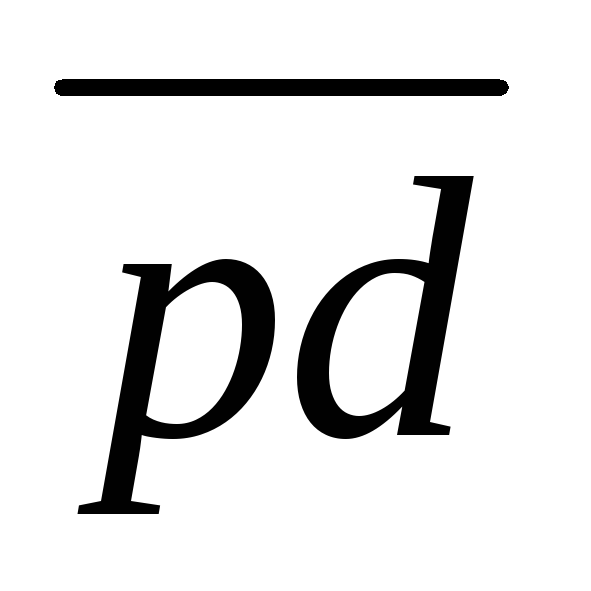в масштабе µ_v изображает скорость V_Д:

План линейных скоростей планетарного механизма можно построить, не определяя его масштаба, задавшись одним вектором линейной скорости (произвольной длины) любой точки механизма.

Для построения плана угловых скоростей. Проводят горизонтальную линию и из любой точки этой линии откладывают вертикальный отрезок EF произвольной длины. Из точки F проводят лучи, параллельные соответствующим прямым плана линейных скоростей (1,2-3,Н). Эти лучи отсекают на горизонтали отрезки, пропорциональные угловым скоростям звеньев зубчатого механизма.

(16)

Значения угловых скоростей получают, умножив соответствую­щий отрезок на масштаб µ_ω:

Передаточное отношение ί_1-Н механизма, используя формулу (1) определяют так:

где │ω₁│ , │ω_Н│ – отрезки с плана угловых скоростей

Таким образом, для определения передаточного отношения механизма можно не определять масштаб плана угловых скоростей.

По плану угловых скоростей определяют не только величину передаточного отношения, но и его знак. Если отрезки / ω₁ / и / ω_Н / расположены относительно EF по одну сторону – передаточное отношение положительно; если по разные стороны – отрицательно.

2.4.2. ЗАМКНУТЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ МЕХАНИЗМЫ

Принцип построения плана линейных скоростей замкнутого дифференциального механизма аналогичен рассмотренному в п. 2.4.1.

Начинать его построение рекомендуется со скорости точки звена, входящего в состав замыкающего механизма.

ПРИМЕР: Дано: ω₇ – угловая скорость колеса 7;

Z_1,2…7 – числа зубьев всех колес и их модуль (m),

Рис.7. Схема и планы скоростей замкнутого дифференциального механизма

Начертив схему механизма в масштабе µ₁ (рис.7) и выбрав ось мгновенных центров скоростей у-у, проектируют на неё точки, лежащие на осях колес. Получают точки 0 и 0₁.

Закон изменения скоростей точек колеса 7

Откладывают от у-у отрезок произвольной длины ре, изображающий в произвольном масштабе вектор скорости точки Е колёс 7 и 6. Прямая оe будет законом изменения скоростей точек колеса 7. Эта же прямая будет законом линейных скоростей точек водила, т.к. водило и колесо 7 жестко закреплены на одной оси. Так как точка В принадлежит водилу, то её скорость определяют, спроектировав эту точку на продолжение линии oe: V_в= *µ_V

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Лекция 15. Кинематика планетарных механизмов.

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков , а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

• однорядный планетарный механизм;
• двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
• двухрядный планетарный механизм с двумя внешними зацеплениями;
• двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется «солнечным»;
• колесо с внутренними зубьями называют «короной» или «эпициклом»;
• колеса, оси которых подвижны, называют «сателлитами»;
• подвижное звено, на котором установлены сателлиты, называют » водилом » . Звено водила принято обозначать не цифрой, а латинской буквой h .

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Типовые планетарные механизмы

Источник