Пифагор способы решения теорем

Доказательства теоремы Пифагора

Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.

Теорема Пифагора — краткая история

Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.

Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Позднее появился алгебраический вариант:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Уравнение

В виде формулы теорема Пифагора записывается следующим образом:

a 2 +b 2 =c 2 , где:

• а и b – длины двух катетов,
• с – длина гипотенузы.

Доказательство через подобные треугольники

Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.

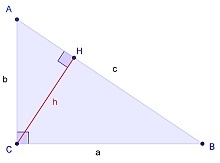
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.

Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:

CB 2 =ABxHB, AC 2 =ABxAH

Сложив между собой квадраты катетов, получаем:

AC 2 +CB 2 =ABx(HB+AH)=AB 2

Это и требовалось доказать.

Другие способы доказательства теоремы

Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.

Методом площадей

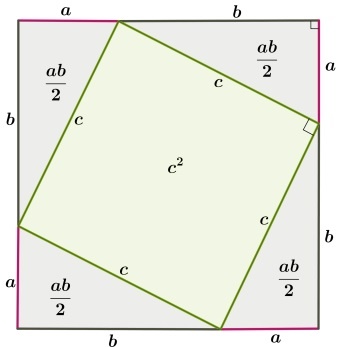
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:

Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.

Площадь внешнего квадрата включает в себя:

• сумму площадей четырех прямоугольных треугольников;
• площадь внутреннего квадрата.

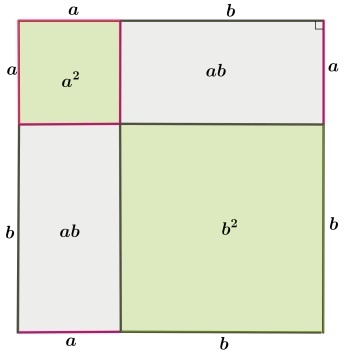
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.

4ab 2 =2ab ⇒ c 2 =a 2 +b 2 , что и нужно было доказать.

Методом бесконечных малых

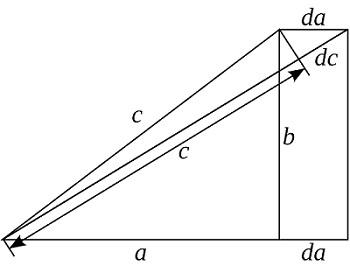
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.

В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем

da/ca = c/a, b = const

Разделяя переменные составляется дифференциальное уравнение:

Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:

c 2 = a 2 + const

определяя из начальных условий константу интегрирования, получим:

a = 0 ⇒ c 2 = b 2 = const

Таким образом мы определяем, что

Следствие из теоремы Пифагора

Его так же называют обратной теоремой Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.

В алгебраическом виде это можно представить так:

c2=a2+b2, где:

• c – гипотенуза треугольника;
• a и b – его катеты.

Применение теоремы

Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.

Расстояние между точками

Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:

• s – необходимое расстояние;
• (a; b) и (с; d) – координаты двух точек.

Евклидова метрика

В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:

• n – число измерений данного пространства;
• d (p, q) – необходимое расстояние;
• p(p₁,….,pn) и q(q₁,….,q_n) – две точки, расстояние между которыми нужно найти.

Теория чисел

Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.

Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.

Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.

Примеры решения задач

Задача 1

В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.

Решение

По теореме Пифагора ВС 2 +АС 2 =АВ 2 , значит

Для нахождения ответа подставим в формулу исходные значения:

Задача 2

Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.

Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:

• 46²+56²= 5252;
• 76²= 5776;
• 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.

Задача 3.

Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.

Решение

Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.

Источник

Различные способы доказательства теоремы Пифагора

учащаяся 9 «А» класса

Теорема Пифагора по праву считается самой важной в курсе геометрии и заслуживает при­стального внимания. Она являет­ся основой решения множества геометрических задач, базой для изучения теоретического и практического курса геометрии в дальнейшем. Теорема окружена богатей­шим историческим материалом, связанным с её появлением и способами доказательства. Изучение истории развития геометрии прививает любовь к данному предмету, способствует развитию познава­тельного интереса, общей культу­ры и творчества, а так же развивает навыки научно-исследовательской работы.

В результате поисковой деятельности была достигнута цель работы, заключающаяся в пополнении и обобщении знаний по доказательству теоремы Пифагора. Удалось найти и рассмотреть различные способы доказательства и углубить знания по теме, выйдя за страницы школьного учебника.

Собранный материал ещё больше убеждает в том, что теорема Пифагора является великой теоремой геометрии, имеет огромное теоретическое и практическое значение.

Введение. Историческая справка 5 Основная часть 8

3. Заключение 19

4. Используемая литература 20
1. ВВЕДЕНИЕ. ИСТОРИЧЕСКАЯ СПРАВКА.

Суть истины вся в том, что нам она — навечно,

Когда хоть раз в прозрении ее увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна.

На радостях богам был Пифагором дан обет:

За то, что мудрости коснулся бесконечной,

Он сто быков заклал, благодаря предвечных;

Моленья и хвалы вознес он жертве вслед.

С тех пор быки, когда учуят, тужась,

Что к новой истине людей опять подводит след,

Ревут остервенело, так что слушать мочи нет,

Такой в них Пифагор вселил навеки ужас.

Быкам, бессильным новой правде противостоять,

Что остается? — Лишь глаза закрыв, реветь, дрожать.

Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что он открыл ее под силь­ным влиянием египетской науки. Частный случай теоре­мы Пифагора — свойства треугольника со сторонами 3, 4 и 5 — был известен строителям пирамид задолго до рожде­ния Пифагора, сам же он более 20 лет обучался у египет­ских жрецов. Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков. Это, однако, противоречит сведениям о моральных и ре­лигиозных воззрениях Пифагора. В литературных источ­никах можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Пифагор питался только медом, хлебом, овощами и изредка рыбой. В связи со всем этим более правдоподобной можно считать следующую запись: «. и даже когда он открыл, что в прямоугольном треугольнике гипо­тенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

Популярность теоремы Пифагора столь велика, что ее доказательства встречаются даже в художественной литературе, например, в рассказе известного английско­го писателя Хаксли «Юный Архимед». Такое же Доказа­тельство, но для частного случая равнобедренного пря­моугольного треугольника приводится в диалоге Плато­на «Менон».

«Далеко-далеко, куда не летают даже самолеты, находится страна Геометрия. В этой необычной стране был один удиви­тельный город — город Теорем. Однажды в этот город пришла красивая девочка по имени Гипотенуза. Она попробовала снять комнату, но куда бы она ни обращалась, ей всюду отказывали. Наконец она подошла к покосившемуся домику и постучала. Ей открыл мужчина, назвавший себя Прямым Углом, и он предло­жил Гипотенузе поселиться у него. Гипотенуза осталась в доме, в котором жили Прямой Угол и два его маленьких сына по имени Катеты. С тех пор жизнь в доме Прямого Угла пошла по-ново­му. На окошке гипотенуза посадила цветы, а в палисаднике развела красные розы. Дом принял форму прямоугольного тре­угольника. Обоим катетам Гипотенуза очень понравилась и они попросили ее остаться навсегда в их доме. Ло вечерам эта друж­ная семья собирается за семейным столом. Иногда Прямой Угол играет со своими детишками в прятки. Чаще всего искать при­ходится ему, а Гипотенуза прячется так искусно, что найти ее бывает очень трудно. Однажды во время игры Прямой Угол подметил интересное свойство: если ему удается найти катеты, то отыскать Гипотенузу не составляет труда. Так Прямой Угол пользуется этой закономерностью, надо сказать, очень успешно. На свойстве этого прямоугольного треугольника и основана тео­рема Пифагора.»

(Из книги А. Окунева «Спасибо за урок, дети»).

Шутливая формулировка теоремы:

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путем

К результату мы придем.

Изучая алгебру и начала анализа и геометрию в 10 классе, я убедилась в том, что кроме рассмотренного в 8 классе способа доказательства теоремы Пифагора существуют и другие способы доказательства. Представляю их на ваше обозрение.
2. ОСНОВНАЯ ЧАСТЬ.

Теорема. В прямоугольном треугольнике квадрат

гипотенузы равен сумме квадратов катетов.

Пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.

Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с (рис.1, а).

Докажем, что с²=а²+в².

Доказательство.

Достроим треугольник до квадрата со стороной а + в так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².

Теорема доказана.
2 СПОСОБ.

После изучения темы «Подобные треугольники» я выяснила, что можно применить подобие треугольников к доказательству теоремы Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота (рис. 2). Докажем, что АС² +СВ² = АВ².

На основании утверждения о катете прямоугольного треугольника:

АС = , СВ = .

Возведем в квадрат и сложим полученные равенства:

АС² = АВ * АD, СВ² = АВ * DВ;

АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда

Доказательство закончено.
3 СПОСОБ.

К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника. Рассмотрим рис. 3.

Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С.

По определению косинуса угла:

cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²

cos В = ВD/ВС = ВС/АВ.

Отсюда АВ * ВD = ВС² .

Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:

Доказательство закончено.
4 СПОСОБ.

Изучив тему «Соотношения между сторонами и углами прямоугольного треугольника», я думаю, что теорему Пифагора можно доказать ещё одним способом.

Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с. (рис. 4).

sinВ= в/с ; cosВ= a/с, то, возведя в квадрат полученные равенства, получим:

Сложив их, получим:

1= (в²+ а²) / с², следовательно,

Данное доказательство основано на разрезании квадратов, построенных на катетах (рис. 5), и укладывании полученных частей на квадрате, по­строенном на гипотенузе.

Для доказательства на катете ВС строим BCD ABC (рис.6 ). Мы знаем, что пло­щади подобных фигур отно­сятся как квадраты их сход­ственных линейных размеров:

Вычитая из первого равенства второе, получим

,

,

с2 = а2 + b2.

ABС, = 90°, ВС = а, АС=b, АВ = с.

Пусть катет b а. Продолжим отре­зок СВ за точку В и построим треугольник BMD так, что­бы точки М и А лежали по одну сторону от прямой CD и, кроме того, BD = b, BDM = 90°, DM = a, тогда BMD = ABC по двум сторонам и углу между ними. Точки А и М соединим отрезками AM. Имеем MD CD и AC CD, значит, прямая АС параллельна прямой MD. Так как MD

Источник