Первым способ двоичного кодирования предложил

История технических способов кодирования информации

С появлением технических средств хранения и передачи информации воз­никли новые идеи и приемы кодиро­вания. Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе.

Просмотр содержимого документа
«История технических способов кодирования информации»

История технических способов кодирований информации

С появлением технических средств хранения и передачи информации воз­никли новые идеи и приемы кодиро­вания. Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе. Телеграфное сообщение — это последо­вательность электрических сигналов, пе­редаваемая от одного телеграфного ап­парата по проводам к другому теле­графному аппарату. Эти технические обстоятельства привели С.Морзе к идее использования всего двух видов сигна­лов — короткого и длинного — кодирования сообщения, передаваемо­го по линиям телеграфной связи.

Такой способ кодирования получил название аз­буки Морзе. В ней каждая буква алфавита кодиру­ется последовательностью коротких сигналов (то­чек) и длинных сигналов (тире). Буквы отделяются друг от друга паузами — отсутствием сигналов.

Жан Морис Эмиль Бодо (1845-1903), Франция

Самым знаменитым телеграфным сообщением яв­ляется сигнал бедствия «SOS» (Save Our Souls — спа­сите наши души). Вот как он выглядит в коде азбуки Морзе, применяемой к английскому алфавиту:

Три точки (буква S), три тире (бук­ва О), три точки (буква S). Две паузы отделяют буквы друг от друга.

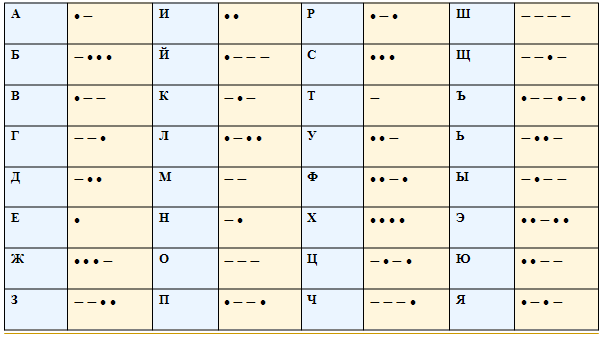
На рисунке показана азбука Морзе применительно к русскому алфавиту. Специальных знаков препинания не было. Их записывали словами: «тчк» — точка, «зпт» — запятая и т.п.

Кодовая таблица азбуки Морзе для русского алфавита

Характерной особенностью азбуки Морзе является переменная длина кода разных букв, поэтому код Морзе на­зывают неравномерным кодом.

Буквы, которые встречаются в тексте чаще, имеют более короткий код, чем редкие буквы. Например, код буквы «Е» — одна точка, а код твердого знака состоит из шести знаков. Это сделано для того, чтобы сократить длину всего сообщения. Но из-за переменной дли­ны кода букв возникает проблема от­деления букв друг от друга в тексте. Поэтому приходится для разделения использовать паузу (пропуск). Следо­вательно, телеграфный алфавит Мор­зе является троичным, т.к. в нем ис­пользуется три знака: точка, тире, пропуск.

Равномерный телеграфный код был изобретен французом Жаном Морисом Бодо в конце XIX века. В нем использовалось всего два разных вида сигналов. Не важно, как их назвать: точка и тире, плюс и минус, ноль и единица. Это два отличающихся друг от дру­га электрических сигнала. Длине кода всех символов одинаковая и равна пяти. В таком случае не возни­кает проблемы отделения букв друг от друга: каж­дая пятерка сигналов — это знак текста. Поэтому пропуск не нужен.

Жан Морис Эмиль Бодо(1845-1903), Франция

Код Бодо — это первый в истории техники спо­соб двоичного кодирования информа­ции. Благодаря этой идее удалось со­здать буквопечатающий телеграфный аппарат, имеющий вид пишущей ма­шинки. Нажатие на клавишу с опре­деленной буквой вырабатывает соот­ветствующий пятиимпульсный сигнал, который передается по линии связи. Принимающий аппарат под воздей­ствием этого сигнала печатаем ту же букву на бумажной ленте.

В современных компьютерах для ко­дирования текстов, также применяет­ся равномерный двоичный код.

Газета «Первое сентября», «Информатика», №12, 2007.

Источник

Бинарный код — Binary code

Двоичный код представляет собой текст , инструкцию , процессор компьютера , или любую другую информацию , используя систему из двух символов. Используемая двухсимвольная система часто представляет собой «0» и «1» из двоичной системы счисления . Двоичный код присваивает шаблон двоичных цифр, также известный как биты , каждому символу, команде и т. Д. Например, двоичная строка из восьми битов может представлять любое из 256 возможных значений и, следовательно, может представлять широкий спектр различных Предметы.

В вычислениях и телекоммуникациях двоичные коды используются для различных методов кодирования данных, таких как символьные строки , в битовые строки. Эти методы могут использовать строки фиксированной или переменной ширины . В двоичном коде фиксированной ширины каждая буква, цифра или другой символ представлены битовой строкой той же длины; эта битовая строка, интерпретируемая как двоичное число , обычно отображается в кодовых таблицах в восьмеричной , десятичной или шестнадцатеричной системе счисления. Существует множество наборов символов и множество кодировок для них.

Битовая строка , интерпретируется как двоичное число, может быть переведен в десятичное число . Например, нижний регистр a , если он представлен битовой строкой 01100001 (как в стандартном коде ASCII ), также может быть представлен как десятичное число «97».

СОДЕРЖАНИЕ

История двоичных кодов

Современная двоичная система счисления, основа двоичного кода, была изобретена Готфридом Лейбницем в 1689 году и фигурирует в его статье Explication de l’Arithmétique Binaire . Полное название переводится на английский как «Объяснение двоичной арифметики», в котором используются только символы 1 и 0, с некоторыми замечаниями о его полезности и о свете, который он проливает на древние китайские фигуры Фу Си »( 1703). В системе Лейбница используются 0 и 1, как в современной двоичной системе счисления. Лейбниц познакомился с И Цзин через французского иезуита Иоахима Буве и с восхищением заметил, как его гексаграммы соответствуют двоичным числам от 0 до 111111, и пришел к выводу, что это отображение было правильным. свидетельство основных достижений Китая в области философской визуальной двоичной математики, которой он восхищался.Лейбниц рассматривал гексаграммы как подтверждение универсальности его собственной религиозной веры.

Двоичные числа занимали центральное место в теологии Лейбница. Он считал, что двоичные числа символизируют христианскую идею creatio ex nihilo или сотворения из ничего. Лейбниц пытался найти систему, которая преобразует словесные утверждения логики в чисто математические. После того как его идеи были проигнорированы, он натолкнулся на классический китайский текст под названием И Цзин или «Книга перемен», в котором использовались 64 гексаграммы шестибитного визуального двоичного кода. Книга подтвердила его теорию о том, что жизнь можно упростить или свести к ряду простых предположений. Он создал систему, состоящую из рядов нулей и единиц. В то время Лейбниц еще не нашел применения этой системе.

Бинарные системы до Лейбница также существовали в древнем мире. Вышеупомянутый И Цзин, с которым столкнулся Лейбниц, датируется IX веком до нашей эры в Китае. Бинарная система И Цзин , текста для гадания, основана на двойственности Инь и Ян . Щелевые барабаны с двоичными тонами используются для кодирования сообщений в Африке и Азии. Индийский ученый Пингала (около 5–2 вв. До н.э.) разработал бинарную систему для описания просодии в своей «Чандашутрам».

Жители острова Мангарева во Французской Полинезии использовали гибридную двоично-десятичную систему до 1450 года. В 11 веке ученый и философ Шао Юн разработал метод расположения гексаграмм, который, хотя и непреднамеренно, соответствует последовательности от 0 до 63. , как представлено в двоичном формате, с инь как 0, ян как 1 и младший бит наверху. Упорядочение также является лексикографическим порядком на шестернях элементов, выбранных из двухэлементного набора.

В 1605 году Фрэнсис Бэкон обсуждал систему, с помощью которой буквы алфавита можно было преобразовать в последовательности двоичных цифр, которые затем можно было закодировать как едва заметные вариации шрифта в любом произвольном тексте. Что важно для общей теории двоичного кодирования, он добавил, что этот метод может быть использован с любыми объектами вообще: «при условии, что эти объекты могут иметь только двукратное различие, как, например, с помощью колоколов, труб, огней и факелов, согласно докладу». мушкетов и любых подобных им инструментов «.

Джордж Буль опубликовал в 1847 году статью под названием «Математический анализ логики», в которой описывается алгебраическая система логики, ныне известная как булева алгебра . Система Буля была основана на бинарном подходе «да-нет», включающем и выключающем, который состоял из трех основных операций: И, ИЛИ и НЕ. Эта система не была введена в эксплуатацию до тех пор , аспиранта из Массачусетского технологического института , Клода Шеннона , заметил , что Булева алгебра он узнал , был подобен электрической цепи. Шеннон написал диссертацию в 1937 году, в которой реализованы его открытия. Диссертация Шеннона стала отправной точкой для использования двоичного кода в практических приложениях, таких как компьютеры, электрические схемы и т. Д.

Другие формы двоичного кода

Битовая строка — не единственный тип двоичного кода: фактически, двоичная система в целом — это любая система, которая допускает только два выбора, например, переключатель в электронной системе или простой тест на истинность или ложь.

Шрифт Брайля

Брайль — это тип двоичного кода, который широко используется слепыми для чтения и записи на ощупь, названный в честь его создателя Луи Брайля. Эта система состоит из сеток из шести точек в каждой, по три на столбец, в которых каждая точка имеет два состояния: поднято или не поднято. Различные комбинации выпуклых и плоских точек могут представлять все буквы, цифры и знаки препинания.

Багуа

В Багуа представлены диаграммы , используемые в фэн — шуй , даосской космологии и я Ching исследований. Ба гуа состоит из 8 триграмм; bā означает 8, а guà означает фигуру гадания. То же слово используется для 64 гуа (гексаграмм). Каждая фигура состоит из трех линий ( yáo ), которые либо прерваны ( инь ), либо не прерваны ( ян ). Отношения между триграммами представлены в двух формах: изначальном багуа «Раннее небо» или «Фукси» и проявленном багуа «Позднее небо» или «Король Вэнь» . (См. Также последовательность 64 гексаграмм короля Вэня ).

Ифа, Ильм аль-Рамл и геомантия

Система гадания Ифа / Ифе в африканских религиях, таких как йоруба , игбо , эве , состоит из сложной традиционной церемонии, производящей 256 оракулов, составленных из 16 символов с 256 = 16 x 16. Посвященный священник « бабалово », который запомнил оракулы, просили жертв у консультантов и возносили молитвы. Затем орехи гадания или пара цепочек используются для получения случайных двоичных чисел, которые рисуются песчаным материалом на фигурном деревянном подносе «Опун», представляющем совокупность судьбы.

Благодаря распространению исламской культуры Ифе / Ифа было ассимилировано как «Наука о песке» (ilm al-raml), которая затем распространилась дальше и стала «наукой чтения знаков на земле» ( геомантия ) в Европе.

Считалось, что это еще один возможный путь, на котором была вдохновлена ​​информатика, поскольку геомантия пришла в Европу на более раннем этапе (около 12 века, описанного Хью Санталла ), чем И Цзин (17 век, описанный Готфридом Вильгельмом Лейбницем ).

Системы кодирования

Код ASCII

Американский стандартный код для обмена информацией (ASCII), использует 7-битный двоичный код для представления текста и других символов внутри компьютеров, оборудования связи и других устройств. Каждой букве или символу присваивается номер от 0 до 127. Например, строчная буква «a» представлена 1100001 как битовая строка (которая в десятичном виде равна «97»).

Десятичное число с двоичным кодом

Десятичное число с двоичным кодированием (BCD) — это двоичное представление целочисленных значений, в котором для кодирования десятичных цифр используется 4-битный полубайт . Четыре двоичных бита могут кодировать до 16 различных значений; но в числах с кодировкой BCD допустимы только десять значений в каждом полубайте и кодируют десятичные цифры от нуля до девяти. Остальные шесть значений являются недопустимыми и могут вызвать либо машинное исключение, либо неопределенное поведение, в зависимости от компьютерной реализации арифметики BCD.

BCD-арифметика иногда предпочтительнее числовых форматов с плавающей запятой в коммерческих и финансовых приложениях, где сложное поведение округления чисел с плавающей запятой неуместно.

Раннее использование двоичных кодов

• 1875: Эмиль Бодо «Добавление двоичных строк в его систему шифрования», что в конечном итоге привело к сегодняшнему ASCII.
• 1884: Машина Linotype, в которой матрицы сортируются по соответствующим каналам после использования направляющей с двоичным кодом.
• 1932: счетчик CE Винна-Вильямса «Шкала двух»
• 1937: электромеханический двоичный умножитель Алана Тьюринга
• 1937: Джордж Стибиц»лишняя тройка» кода в сложном компьютере.
• 1937: Компьютер Атанасова-Берри
• 1938: Конрад ЦузеZ1

Текущее использование двоичного кода

Большинство современных компьютеров используют двоичное кодирование для инструкций и данных. Компакт-диски , DVD-диски и диски Blu-ray представляют звук и видео в цифровом виде в двоичной форме. Телефонные звонки передаются в цифровом виде по междугородним и мобильным телефонным сетям с использованием импульсно-кодовой модуляции , а также по IP- сетям.

Вес двоичных кодов

Вес двоичного кода, как определено в таблице кодов с постоянным весом , является весом Хэмминга двоичных слов, кодирующих представленные слова или последовательности.

Источник

Первым способ двоичного кодирования предложил

Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером и так далее. Информация, поступает в виде условных знаков или сигналов самой разной физической природы.

Это свет, звук, запах, касания; это слова, значки, символы, жесты и движения.

Для того чтобы произошла передача информации, мы должны не только принять сигнал от кого-то, но и расшифровать его.

Так, услышав звонок будильника, человек понимает, что пришло время просыпаться;

телефонный звонок — кому-то нужно с нами поговорить;

школьный звонок сообщает учащимся о долгожданной перемене.

Для правильного понятия разных сигналов требуется разработка кода или кодирование.

Код — это система условных знаков для представления информации.

Кодирование — это перевод информации в удобную для передачи, обработки или хранения форму с помощью некоторого кода.

Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.

В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре происходит кодирование знака, то есть преобразование его в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс — декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение.

Обратное преобразование называется декодированием.

Декодирование — это процесс восстановления содержания закодированной информации.

Можно рассмотреть в качестве примера кодирования соответствие цифрового и штрихового кодов товара. Такие коды имеются на каждом товаре и позволяют полностью идентифицировать товар (страну и фирму производителя, тип товара и др.).

Знакам цифрового кода (цифрам) соответствуют группы знаков штрихового кода (узкие и широкие штрихи, а также размеры промежутков между ними) — рис. Для человека удобен цифровой код, а для автоматизированного учета -штриховой код, который считывается с помощью узкого светового луча и подвергается последующей обработке в компьютерных бухгалтерских системах учета.

Существует три основных способа кодирования информации:

●Числовой способ — с помощью чисел.

●Символьный способ — информация кодируется с помощью символов того же алфавита, что и исходящий текст.

●Графический способ — информация кодируется с помощью рисунков или значков.

Существует равномерное и неравномерное кодирование. При равномерном кодировании сообщение декодируется однозначно. При неравномерном кодировании для однозначного декодирования сообщения нужно, чтобы выполнялось прямое и обратное условие Фано(прямое: никакой код не должен быть началом другого кода, обратное: никакой код не должен быть концом другого кода)

Понимать, что мы можем закодировать сообщение, даже если условие Фано не выполняется, но возможно не сможем его однозначно декодировать.

Однозначно декодировать –получить один единственный точный вариант.

Двоичное кодирование информации в компьютере.

В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежно работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр):

· электромагнитные реле (замкнуто/разомкнуто), широко использовались в конструкциях первых ЭВМ;

· участок поверхности магнитного носителя информации (намагничен/размагничен);

· участок поверхности лазерного диска (отражает/не отражает);

· триггер, может устойчиво находиться в одном из двух состояний, широко используется в оперативной памяти компьютера.

Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц —

Цифры двоичного кода можно рассматривать как два равновероятных состояния (события). При записи двоичной цифры реализуется выбор одного из двух возможных состояний (одной из двух цифр) и, следовательно, она несет количество информации, равное 1 биту.Даже сама единица измерения количества информации бит (bit) получила свое название от английского словосочетания BinarydigiT (двоичная цифра).Важно, что каждая цифра машинного двоичного кода несет информацию в 1 бит. Таким образом, две цифры несут информацию в 2 бита,три цифры — в 3 бита и так далее. Количество информации в битах равно количеству цифр двоичного машинного кода.

Кодирование текстовой информации.

Текстовую информацию кодируют двоичным кодом через обозначение каждого символа алфавита определенным целым числом. С помощью восьми двоичных разрядов возможно закодировать 256 различных символов. Данного количества символов достаточно для выражения всех символов английского и русского алфавитов.

Для английского языка — Институт стандартизации США выработал и ввел в обращение систему кодирования ASCII (AmericanStandardCodeforInformationInterchange – стандартный код информационного обмена США).

Для кодировки русского алфавита были разработаны несколько вариантов кодировок:

1) Windows-1251 – введена компанией Microsoft — в Российской Федерации она нашла широкое распространение.

2) КОИ-8 (Код Обмена Информацией, восьмизначный) – другая популярная кодировка российского алфавита, распространенная в компьютерных сетях.

3) ISO (InternationalStandardOrganization – Международный институт стандартизации) – международный стандарт кодирования символов русского языка. На практике эта кодировка используется редко.

Ограниченный набор кодов (256) создает трудности для разработчиков единой системы кодирования текстовой информации. Вследствие этого было предложено кодировать символы не 8-разрядными двоичными числами, а числами с большим разрядом, что вызвало расширение диапазона возможных значений кодов. Система 16-разрядного кодирования символов называется универсальной – UNICODE.

Кодирование графической информации.

Существует несколько способов кодирования графической информации.

поэтому способ растрового кодирования базируется на использовании двоичного кода представления графических данных. Общеизвестным стандартом считается приведение черно-белых иллюстраций в форме комбинации точек с 256 градациями серого цвета, т. е. для кодирования яркости любой точки необходимы 8-разрядные двоичные числа.

В основу кодирования цветных графических изображений положен принцип разложения произвольного цвета на основные составляющие, в качестве которых применяются три основных цвета: красный (Red), зеленый (Green) и синий (Blue). На практике принимается, что любой цвет, который воспринимает человеческий глаз, можно получить с помощью механической комбинации этих трех цветов. Такая система кодирования называется RGB. При применении 24 двоичных разрядов для кодирования цветной графики такой режим носит название полноцветного (TrueColor).

Для любого из основных цветов дополнительным будет являться цвет, который образован суммой пары остальных основных цветов. Соответственно среди дополнительных цветов можно выделить голубой (Cyan), пурпурный (Magenta) и желтый (Yellow). Принцип разложения произвольного цвета на составляющие компоненты используется не только для основных цветов, но и для дополнительных. Этот метод кодирования цвета применяется в полиграфии, но там используется еще и четвертая краска – черная (Black), поэтому эта система кодирования обозначается четырьмя буквами – CMYK. Для представления цветной графики в этой системе применяется 32 двоичных разряда. Данный режим также носит название полноцветного.

Кодирование звуковой информации.

В настоящий момент не существует единой стандартной системы кодирования звуковой информации, так как приемы и методы работы со звуковой информацией начали развиваться по сравнению с методами работы с другими видами информации самыми последними. Поэтому множество различных компаний, которые работают в области кодирования информации, создали свои собственные корпоративные стандарты для звуковой информации. Но среди этих корпоративных стандартов выделяются два основных направления.

В основе метода FM (FrequencyModulation) положено утверждение о том, что теоретически любой сложный звук может быть представлен в виде разложения на последовательность простейших гармонических сигналов разных частот. Каждый из этих гармонических сигналов представляет собой правильную синусоиду и поэтому может быть описан числовыми параметрами или закодирован. Звуковые сигналы образуют непрерывный спектр. Обратное преобразование, которое необходимо для воспроизведения звука, закодированного числовым кодом, производится с помощью цифроаналоговых преобразователей (ЦАП). Из-за таких преобразований звуковых сигналов возникают потери информации, которые связаны с методом кодирования, поэтому качество звукозаписи с помощью метода FM обычно получается недостаточно удовлетворительным. Этот метод широко использовался в те годы, когда ресурсы средств вычислительной техники были явно недостаточны.

Основная идея метода таблично-волнового синтеза (Wave-Table) состоит в том, что в заранее подготовленных таблицах находятся образцы звуков для множества различных музыкальных инструментов. Данные звуковые образцы носят название сэмплов. Числовые коды, которые заложены в сэмпле, выражают такие его характеристики, как тип инструмента, номер его модели, высоту тона и тд. Поскольку для образцов применяются реальные звуки, то качество закодированной звуковой информации получается очень высоким и приближается к звучанию реальных музыкальных инструментов, что в большей степени соответствует нынешнему уровню развития современной компьютерной техники.

Множество кодов очень прочно вошло в нашу жизнь.

●числовая информация кодируется арабскими, римскими цифрами и др.

●для общения и письма мы используем код — русский язык, в Китае — китайский и т.д.

●с помощью нотных знаков кодируется любое музыкальное произведение, а на экране проигрывателя вы можете увидеть громкий или тихий звук, закодированный с помощью графика.

●часто бывает так, что информацию надо сжать и представить в краткой, но понятной форме. Тогда применяют пиктограммы, например, на двери магазина, на столбах в парке, на дороге.

Для передачи информации, людьми были придуманы специальные коды, к ним относятся:

Источник