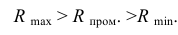Пересечение поверхности способом вспомогательной сферы

Пересечение поверхности способом вспомогательной сферы

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

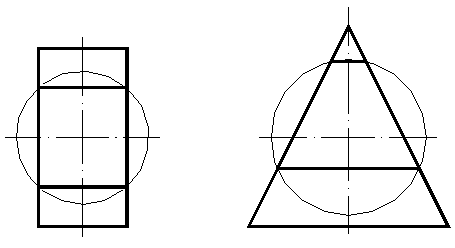
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей — прямые линии, а второй — когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

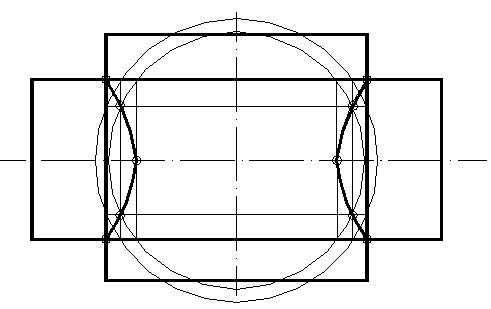
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

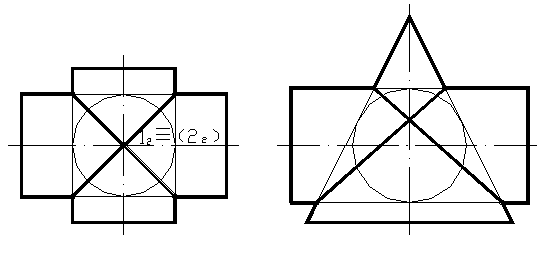
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

4.4. Способ вспомогательных секущих сфер.

Для построения линии пересечения некоторых поверхностей рациональнее применять в качестве вспомогательных секущих поверхностей-посредников – сферы.

Пример№2. Построить линию пересечения тора с цилиндром вращения.

Решение. Так как обе заданные поверхности являются поверхностями вращения, оси которых пересекаются в точке О (O₁; О₂) и параллельны фронтальной плоскости проекций, то применяем метод концентрических сфер. Приняв точку О за центр сфер, описываем одну из них (рис. 244). Она пересекает обе поверхности по окружностям, фронтальные проекции которых есть отрезки А₂В₂, С₂Е₂ прямых. Точки I₂, II₂ пересечения этих отрезков будет принадлежать фронтальной проекции искомой линии пересечения. Горизонтальные проекции I₁, II₁ точек I и II находим обычным образом. Вспомогательные сферы проводим между максимальной и минимальной сферами. R_max равен отрезку O₂K₂, R_min равен наибольшему из перпендикуляров, опущенных из точки О₂ на очерковые образующие. Найдя достаточное количество точек, соединим их плавной лекальной кривой.

Источник

Метод сфер | AutoCAD

Еще один метод построения линии пересечения поверхностей вращения – метод сфер. Он применяется в случаях, когда метод секущих плоскостей использовать нецелесообразно – например, когда оси одной или обеих поверхностей вращения расположены так, что при пересечении этих поверхностей с плоскостями, параллельными плоскостям проекций, образуются сложные фигуры. Один из таких случаев – когда оси поверхностей вращения пересекаются в пространстве. Пусть одна из поверхностей – цилиндр, а вторая – тело вращения, образованное кривой 2-го порядка. Оговоримся, что для применения метода сфер необходимо привести чертеж к такому виду, когда оси вращения обеих поверхностей параллельны одной из плоскостей проекций.

1. Пусть исходный чертеж выглядит так:

2. При построениях такого рода целесообразно применять концентрические сферы-посредники, центры которых расположены в точке пересечения осей исходных тел вращения. Эти сферы, пересекаясь с исходными телами, образуют окружности, а искомые точки линии пересечения будут общими точками пар окружностей, принадлежащим двум телам. Построим «крайние» сферы – самую большую и самую малую из всего диапазона. Видно, что самая большая из сфер пройдет через наиболее удаленную от центра точку пересечения поверхностей, а самая малая будет касаться «внутренней» поверхности одного из тел (сферы меньшего диаметра уже не пересекают оба тела, т.е. в построении не участвуют).

Эти сферы дадут нам первые точки пересечения поверхностей. Находим их так: сначала строим линии пересечения сферы-посредника с каждым из тел на фронтальном виде. Эти линии – окружности, которые на фронтальном виде превращаются в прямые:

3. Пересечение двух линий, образованных одной сферой, даст соответствующую точку искомой линии пересечения поверхностей (поскольку линия симметрична относительно вертикальной плоскости, в которой лежат оси обоих тел, на фронтальном виде будем строить только видимую часть линии. Итак, вот две первые точки:

Переносим эти точки на вид сверху. Здесь важно понимать следующее: точки лежат на окружностях, образованных пересечением сфер-посредников с каждым из тел, причем это утверждение справедливо для любых проекций. Поэтому нам нужно построить эти окружности на виде сверху для любого из тел (очевидно, что цилиндр в этом случае неудобен, поскольку его ось наклонена) и перенести на них точки с фронтального вида. Сферы, изображенные на виде сверху, можно удалить, чтобы они не мешали построениям:

4. Построим еще несколько сфер-посредников, охватывающих всю область пересечения тел. Одна из сфер должна пройти через вторую «пиковую» точку – самую нижнюю точку пересечения поверхностей. Кстати, строить эту сферу необязательно – эта точка, как и верхняя, явно видна на чертеже. Вот результаты построений для фронтальной проекции:

И для вида сверху:

Для того, чтобы не запутаться в множестве линий построения, можно удалять их после нахождения каждой точки. Также полезно выделить точки, находящиеся на виде сверху ниже «границы видимости», другим цветом. Эти точки на фронтальном виде расположены ниже оси цилиндра. Точка, отделяющая «нижние» точки от «верхних», лежит на оси цилиндра. В нашем случае она практически совпадает с точкой, лежащей на малой сфере, вообще же она требует отдельного построения:

После соединения полученных точек командой Spline и удаления всех вспомогательных линий получим такие результаты:

Стоит отметить, что команда Spline может не сразу дать правильное отображение линии пересечения, особенно на виде сверху. Может оказаться целесообразным рисовать отдельно «правую» и «левую» части кривой.

5. Осталось только сравнить наши построения с пересечением двух поверхностей, которое Autocad строит автоматически. Для этого изобразим исходные тела с помощью команд 3D-моделирования, объединим их и расположим рядом с полученными чертежами:

Как видим, метод сфер позволяет достаточно адекватно изображать пересечение сложных поверхностей вращения. И хотя сегодня он носит достаточно иллюстративный характер, разобраться в нем очень полезно для понимания основ геометрии и трехмерного моделирования.

Источник

Способ вспомогательных сфер в начертательной геометрии с примером

Способ вспомогательных сфер:

Этот способ широко используется при решении задач на построе­ние линий пересечения поверхностей вращения с пересекающимися осями.

Прежде чем перейти к рассмотрению этого способа, рассмотрим частный случай пересечения поверхностей вращения, у которых оси совпадают. Такие поверхности называются соосными поверхностями вращения.

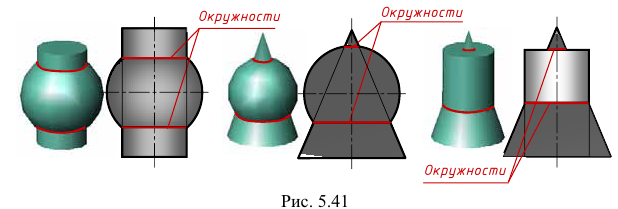
Линия пересечения соосных поверхностей — окружность, плос­кость которой перпендикулярна оси поверхностей вращения. При этом, если ось поверхностей вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой ли­нии (рис. 5.41).

Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические (построенные из одного центра) и эксцентрические (проведенные из разных цен­тров) сферы. Рассмотрим применение вспомогательных концентрических сфер — сфер с постоянным центром.

Следует отметить, что если плоскость осей поверхностей враще­ния не параллельна плоскости проекций, то окружности, по которым пересекаются поверхности, будут проецироваться в эллипсы, а это усложняет решение задачи. Поэтому способ вспомогательных сфер следует применять при следующих условиях:

• а) пересекающиеся поверхности должны быть поверхностями вращения;
• б) оси этих поверхностей должны пересекаться, точку пересечения принимают за центр вспомогательных сфер;
• в) плоскость, образованная осями поверхностей (плоскость сим­метрии), должна быть параллельна одной из плоскостей проекций.

Используя этот способ, можно построить линию пересечения по­верхностей на одной проекции.

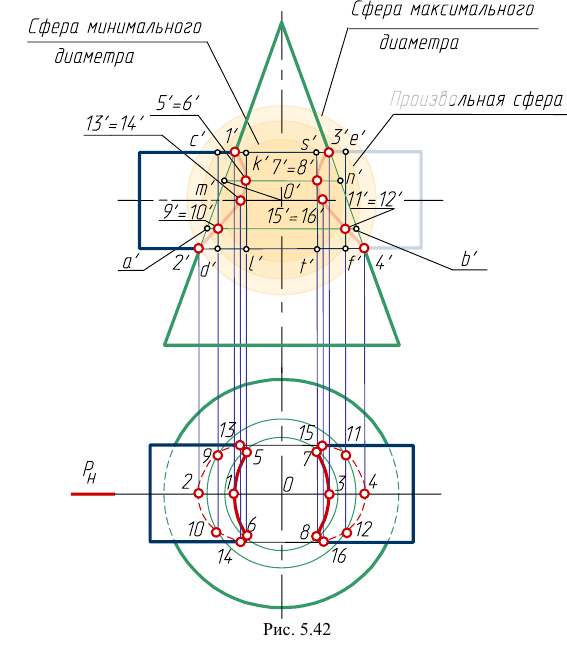
Рассмотрим пример построения линии пересечения цилиндра и конуса вращения (рис. 5.42).

Точки 1, 2, 3, 4 определяются как точки пересечения контурных образующих поверхностей, принадлежащие плоскости пересечения осей (плоскости симметрии

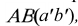
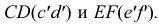
Из точки пересечения осей данных поверхностей (точки О’) построим вспомогательную сферу произвольного радиуса. Эта сфера будет одновременно соосна конусу и цилиндру и пересечет их по окруж­ностям. Плоскости этих окружностей перпендикулярны соответствующим осям вращения. Фронтальные проекции этих окружностей — отрез­ки прямых. Проведенная сфера пересекает конус по окружности диаметра а цилиндр — по окружностям В пересечении окружности АВ с окружностями CD и EF получаем соответственно точки 9-10 и 1 1-12, принадлежащие линии пересечения.

Таким образом, можно построить достаточное количество точек искомой линии пересечения. При этом нужно иметь ввиду, что не все сферы могут быть использованы для решения задачи. Рассмотрим предельные границы вспомогательных сфер.

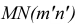
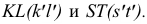
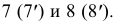
Радиус максимальной секущей сферы будет равен расстоянию от центра о’ до самой удаленной точки пересечения контурных образующих (от точки о’ до точек 2′ и 4′)- Минимальной секущей сферой долж­на быть такая сфера, которая касалась бы одной поверхности (большей) и пересекала вторую (меньшую). В данном примере минимальная сфера касается поверхности конуса по окружности и пересекает ци­линдр по окружностям Пересекаясь между собой, ок­ружности MN и KL дают точки линии пересечения 5 (5′) и 6 (6′), а окружности MN и ST — точки Это самые глубокие точки линии пересечения.

Для точности решения между максимальной и минимальной сфе­рами необходимо построить дополнительные (промежуточные) сферы:

Если дополнительная сфера пересекает только одну данную поверхность, то такая сфера для решения задачи непригодна.

Для построения второй проекции линии пересечения можно ис­пользовать окружности, полученные от сечения конуса вспомогательными сферами.

Можно также построить дополнительные сечения поверхности, Точки 13-14 и 15-16, лежащие на контурных образующих цилиндра, являются точками границы видимости линии пересечения на горизонтальной проекции.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Выполнение и оформление чертежей по ГОСТ и ЕСКД
• Виды в инженерной графике
• Разрезы в инженерной графике
• Сечения в инженерной графике
• Развертка поверхности конуса
• Шаровая поверхность
• Винтовые поверхности
• Способ вспомогательных секущих плоскостей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник