Пересечение поверхностей вращения способ плоскостей уровня

Метод плоскостей уровня. Взаимное пересечение поверхностей вращения

Этот способ применяют для построения линии пересечения поверхностей, пересекающихся с плоскостью по графически простым линиям (прямые или окружности).

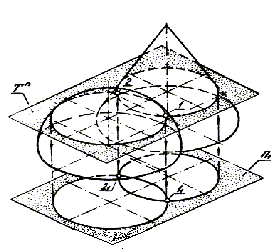
На рисунке 6.21 показано построение проекций линии пересечения поверхностей сферы и закрытого тора..

В качестве посредников применены горизонтальные плоскости уровня, пересекающие обе заданные поверхности по окружностям. Построение начато с определения характерных точек. Так как центр сферы и ось вращения тора, как видно из рисунка, лежат в одной фронтальной плоскости, то в этой плоскости лежат и фронтальные меридианы пересекающихся поверхностей. Эти меридианы пересекаются в точках 1 и 2, являющихся высшей и низшей точками кривой. Точки линии пересечения, принадлежащие экватору сферы, определяют границы видимости горизонтальной проекции линии пересечения. Эти точки (3 и 4) построены с помощью горизонтальной плоскости уровня Г.

Плоскость Г рассекает поверхность сферы по экватору, а поверхность тора по окружности радиуса О₂ К₂. Точки пересечения 3₁ и 4₁ горизонтальных проекций этих окружностей отделяют видимую часть проекции линии пересечения от невидимой.

С помощью горизонтальной плоскости уровня Г 1 построены проекции точек 5 и 6. Горизонтальные проекции 5₁ и 6₁ этих точек определяют места касании горизонтальной проекции линии пересечения и тора. Для построения промежуточных точек 7, 8, 9 и 10 использованы горизонтальные плоскости Г 2 и Г 3 , пересекающих обе поверхности по параллелям.

Источник

Пересечение поверхностей. Метод секущих плоскостей

Пересечение поверхностей. Метод секущих сфер.

Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.

В частном случае, если одна из поверхностей вращения – сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей.

Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:

1. Способом концентрических сфер;

2. Способом эксцентрических сфер.

Способ концентрических сфер.

Этот способ применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхностей вращения, была параллельной какой0либо плоскости проекции.

Способ эксцентрических сфер.

Способ эксцентрических сфер может быть использован для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии. При этом каждая поверхность, имеющих общую плоскость симметрии. При этом каждая поверхность должна иметь семейство окружностей. Как и в способе концентрических сфер, плоскость симметрии должна быть параллельна одной из плоскостей проекции.

Способ эксцентрических сфер можно применять и в тех случаях, когда из пересекающихся поверхностей не является поверхностью вращения. Необходимым условием является наличие на этой поверхности семейства окружностей, которые можно рассматривать как результат пересечения поверхности со сферой. В число условий входит также условие, чтобы перпендикуляры, восстановленные из центров круговых сечений, пересекали ось поверхности вращения.

Пересечение поверхностей. Метод секущих плоскостей.

В качестве поверхностей-посредников используют секущие плоскости. Этот способ применяется в тех случаях, когда можно найти в качестве поверхностей-посредников такие плоскости, которые пересекали бы обе заданные поверхности по геометрически простым линиям — окружностям и прямым (рис. 21). Чаще всего в качестве вспомогательных секущих плоскостей выбираются плоскости уровня, то есть плоскости, параллельные плоскостям проекций. Следует отметить, что способ вспомогательных секущих плоскостей применяется во всех случаях, то есть каждая из пересекающихся поверхностей может быть как гранной, так и поверхностью вращения.

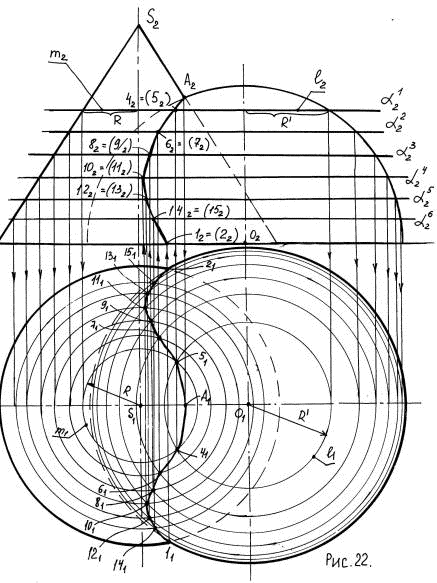
На чертеже (рис. 21, 22) прямой конус вращения пересекается с полусферой.

Построение проекций линии взаимного пересечения поверхностей осуществляется в следующей последовательности:

Определяют на чертеже положения опорных точек кривой пересечения. Фронтальная проекция A2 самой высшей точки кривой пересечения определяется на пересечении главных меридианов пересекающихся поверхностей: для конуса главным меридианом является очерковый треугольник, а для полусферы — очерковая полуокружность во фронтальной плоскости проекций.

Проведя линию связи из точки A2 до пересечения с горизонтальной проекций главных меридианов, получаем горизонтальную проекцию A1 самой высшей точки кривой пересечения. То обстоятельство, что основания фигур располагаются непосредственно в горизонтальной плоскости проекций (рис. 22) позволяет выявить положения самых низших точек 1 и 2 кривой пересечения.

Действительно, точки 11 и 21 пересечения проекций оснований фигур являются горизонтальными проекциями самых низших точек 1 и 2 кривой персечения. Их фронтальные проекции 12 и 22 располагаются на оси ОХ и определяются пересечением оси ОХ с линиями связи, проведенными из точек 11 и 21. В тоже время по отношению к наблюдателю точки 1(11;12) и 2(21;22) являются самой близкой и самой дальней точками кривой пересечения соответственно.

Все точки, кроме A, 1 и 2 являются регулярными точками кривой пересечения. Для определения на чертеже положения их проекций используют способ вспомогательных секущих плоскостей. При этом необходимо удачно выбрать положение секущей плоскости. Это положение выбирают таким образом, чтобы в сечении каждой из заданных поверхностей вращения получались графически простые линии — прямые или окружности.

В данной задаче в качестве вспомогательных секущих плоскостей выбирают горизонтальные плоскости уровня, так как они пересекают обе поверхности: конус и полусферу, по графически простым линиям — окружностям. На чертеже проводят одну секущую плоскость α1, задав ее фронтальным следом α21. Далее строят проекции параллелей — окружностей сечения секущей плоскостью α1 конуса и полусферы. На чертеже фронтальные проекции этих параллелей l2 и m2 располагаются на следе α21 секущей плоскости α1.

Горизонтальные проекции l1 и m1 этих параллелей представляют собой окружности с центрами S1 и O1, радиусами R и R′ соответственно. В пересечении горизонтальных проекций l1 и m1 параллелей получают горизонтальные проекции 41 и 51 регулярных точек кривой пересечения. Проведя линии связи из точек 41 и 51 до пересечения со следом α21 секущей плоскости α1, получают фронтальные проекции 42 и 52 кривой пересечения. Построенные точки 4(41; 42) и 5(51; 52) являются регулярными точками кривой пересечения. Аналогичным образом проводят несколько ниже секущие плоскости α2 — α6, задав их на чертеже фронтальными следами α22 — α26, и строят регулярные точки 6(61; 62) — 15(151; 152) кривой пересечения поверхностей.

После построения на чертеже проекций опорных и регулярных точек кривой соединяют их одноименные проекции плавной кривой (при помощи лекала) и получают горизонтальную и фронтальную проекции кривой взаимного пересечения заданных поверхностей. По чертежу устанавливают, что конус и полусфера имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Тогда горизонтальные проекции точек кривой пересечения окажутся расположенными симметрично относительно горизонтального следа главной меридианальной плоскости, являющейся общей для обеих фигур.

Фронтальные проекции точек кривой пересечения будут совпадать, так как в этом случае они являются конкурирующими по отношению к фронтальной плоскости проекций. Причем проекции точек, расположенных перед главной меридианальной плоскостью фигур, будут видимыми на фронтальной плоскости проекций, а расположенных за ней — невидимыми. Горизонтальные проекции точек кривой пересечения являются видимыми, поэтому горизонтальная проекция кривой пересечения проводится на чертеже сплошной линией.

В заключение отметим, что способ вспомогательных секущих плоскостей уровня используется тогда, когда оси вращения обеих поверхностей (если обе поверхности являются поверхностями вращения) располагаются перпендикулярно одной из плоскостей проекций.

В том случае, когда при пересечении обеих поверхностей одной секущей плоскостью невозможно получить в сечениях графически простые линии — прямые или окружности применяется способ вспомогательных секущих сфер.

Источник

Пересечение поверхностей вращения плоскостью с примерами

Содержание:

Пересечение поверхностей вращения плоскостью:

Линия пересечения кривой поверхности с плоскостью представляет собой плоскую кривую, которая может распадаться и на прямые линии в случае пересечения плоскости с линейчатой поверхностью по ее образующим.

Для построения этой кривой линии на чертеже находят проекции ее отдельных точек, соединяемых с помощью лекала.

Среди точек линии пересечения имеются точки, которые занимают особое расположение на кривой или выделяются своим местоположением относительно плоскостей проекций. Такие точки называют опорными или характерными. К ним относятся высшие и низшие, ближние и дальние, точки, расположенные на крайних образующих (точки видимости) и др.

Остальные точки называются промежуточными или случайными.

Для нахождения точек линии пересечения применяются вспомогательные секущие плоскости (проецирующие или плоскости уровня).

Вспомогательные плоскости выбираются так, чтобы в пересечении с кривой поверхностью получались простейшие линии — прямые и окружности.

Пересечение цилиндра плоскостью

При пересечении цилиндра вращения плоскостью возможны случаи:

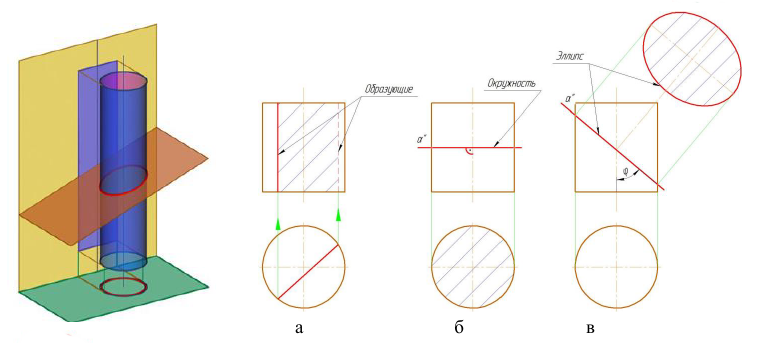
• секущая плоскость параллельна оси — в сечении цилиндрической поверхности полу-чаются две прямые (образующие) (рис. 8.1а);
• секущая плоскость перпендикулярна оси — в сечении получается окружность, равная окружностям оснований (рис. 8.1б);
• секущая плоскость наклонна к оси — в сечении получается эллипс, малая ось которого всегда равна диаметру цилиндра, а большая зависит от угла ϕ (рис. 8.1в).

Рисунок 8.1 — Пересечение цилиндра плоскостью

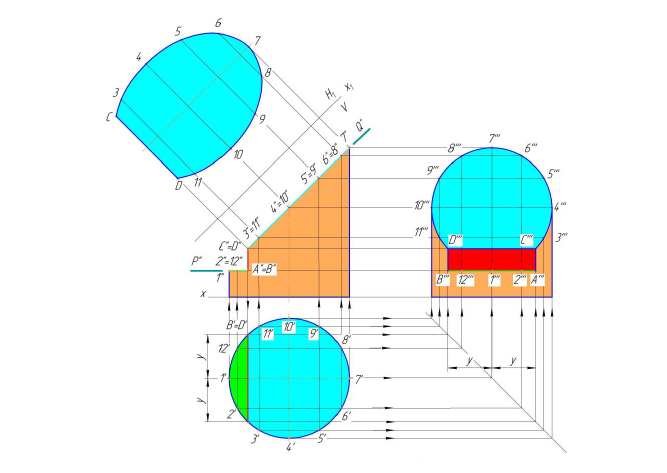
Горизонтальная плоскость Р (Р») пересекает поверхность цилиндра по части окружности, профильная плоскость T (T») по прямым АВ и CD (образующим цилиндра), фронтально-проецирующая плоскость Q (Q») — по части эллипса [5]. Фронтальная проекция линий пересечения совпадает со следами — проекциями секущих плоскостей (P «, T «, Q»), а горизонтальная — с окружностью оснований цилиндра (рис. 8.2).

Рисунок 8.2 — Построение проекций усеченной части цилиндра

Построение профильной проекции сводится к построению профильных проекций точек по двум заданным, направление построений линий связи указано стрелками). Вместо ломаных линий связи при построении профильных проекций точек можно использовать координаты y , которые откладываются на горизонтальных линиях связи по разные стороны оси цилиндра (см. построение точек А, В, С, D).

Обычно для построения точек линий сечения пользуются образующими, равноотстоящими друг от друга. Поэтому горизонтальная проекция цилиндра (окружность) разделена на 12 частей (точки 1, 2. 12). Этой равномерной «разметкой» удобно пользоваться не только для построения проекций сечений, но и для построения развертки.

Действительный вид фигуры сечения плоскостью Q построен способом перемены плоскостей проекций. Новая ось проекций х1 проведена параллельно следу — проекции Q». Выполнив соответствующие построения на плоскости H1, получим натуральную величину сечения цилиндра плоскостью Q.

Пересечение конуса плоскостью

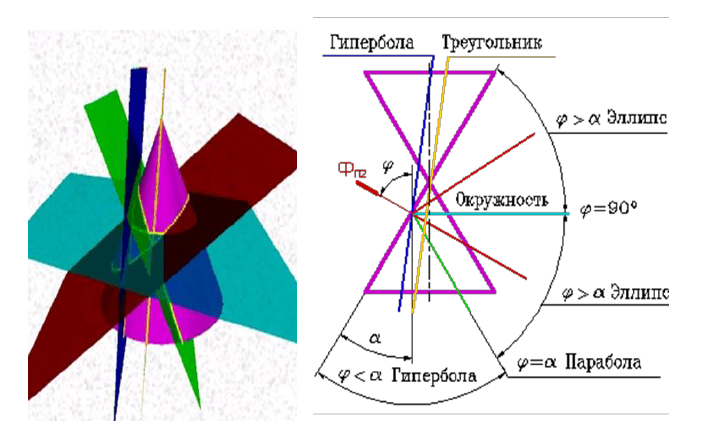
В зависимости от положения секущей плоскости линиями сечения конической поверхности (рис. 8.3) могут быть: эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка.

Рисунок 8.3 — Пересечение конуса плоскостью

Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс. В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.

В частном случае (φ=90) такая плоскость пересекает поверхность конуса по окружности; и сечение вырождается в точку, если плоскость проходит через вершину конуса.

Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ=α, то линией пересечения является парабола. В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую.

Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ δ) (рис. 8.4 а).

В частности, если секущая плоскость перпендикулярна оси конуса, то получается окружность (рис. 8.4 б).

В частном случае, если секущая плоскость проходит через вершину конуса, то в сечении получается пара пересекающихся в вершине прямых (образующих) (рис. 8.4 в).

Секущая плоскость α (α») параллельная одной образующей конуса в сечении получается парабола (φ = φ) (рис. 8.5 а).

Секущая плоскость α1 (α1″) параллельна двум образующим конуса- в се-чении получается гипербола (φ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник