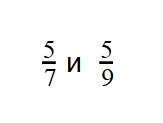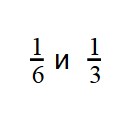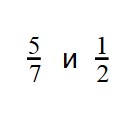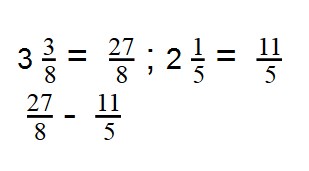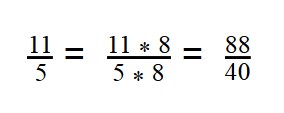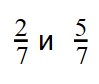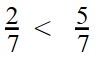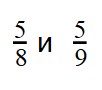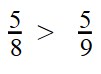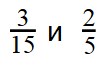Перекрестный способ сравнения дробей

Сравнение дробей, как правильно

О чем эта статья:

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

• Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
  8 8
• Это значит, что 10
  1

Пример 3. Сравните дроби:

• Знаменатели дробей снова равны. Сравниваем числители:
  3 > 1
  1

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

• Запишем в виде дробей: и
• А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
  6 > 5
  5

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  9 > 7
  7 10
• Значит дробь с меньшим знаменателем — больше:
  

Пример 3. Сравните дроби:

У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

• Нужно подобрать число, которое будет делиться на 7 и на 2 (найти наименьшее общее кратное НОК). В данном случае, НОК — 14. Проверим:
  14:7 = 2
  14 : 2 = 7
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 7:
  
• Дроби приведены к общему знаменателю:
  

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

• Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
  30 : 15 = 2
  30 : 2 = 15
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 15:
  
• Дроби приведены к общему знаменателю:
  
• Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
  

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

• 6/5 — неправильная дробь.
• Выделим целую часть:
• Значит, что

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

• 12 — 7 = 6
  12 — уменьшаемое
  7 — вычитаемое
  5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

• 

Вычитаемая дробь меньше уменьшаемой

• Выполняем вычитание:

Пример 2.Найдите разность:

• Смешанные дроби превращаем в неправильные:
  
• Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю:
  
• Наименьшее общее кратное — 40
  40 : 8 = 5
  40 : 5 = 8
• Умножаем первую дробь на дополнительный множитель 5:
  
• Умножаем вторую дробь на дополнительный множитель 8:
  
• Дроби приведены к общему знаменателю:
  

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

• Мы видим, что вычитаемое меньше уменьшаемого, значит можем без труда найти разность:
  

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.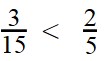

• По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
  
• Наименьшее общее кратное — 15:
  15 : 15 = 1
  15 : 5 = 3
• Умножаем первую дробь на дополнительный множитель 1:
  
• Умножаем вторую дробь на дополнительный множитель 3:
  
• Дроби приведены к общему знаменателю:
  
• Сравниваем числители получившихся дробей: 3

Источник

Перекрестный способ сравнения дробей. Сравнение дробей: правила, примеры, решения

Сравнение дробей: правила, примеры, решения.

В центре внимания данной статьи стоит сравнение дробей. Мы уже знаем про равные и неравные дроби. Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.

Навигация по странице.

Сравнение дробей с одинаковыми знаменателями

Сравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3 доли 1/7 , а дробь 8/7 соответствует 8 долям 1/7 , поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8 , то есть, к сравнению числителей.

Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.

Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.

Какая дробь больше: 65/126 или 87/126 ?

Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87 дроби 87/126 больше числителя 65 дроби 65/126 (при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126 больше дроби 65/126 .

.

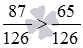
Сравнение дробей с разными знаменателями

Сравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю.

Итак, чтобы сравнить две дроби с разными знаменателями, нужно

• привести дроби к общему знаменателю;
• сравнить полученные дроби с одинаковыми знаменателями.

Разберем решение примера.

Сравните дробь 5/12 с дробью 9/16 .

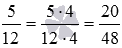
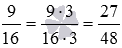
Сначала приведем данные дроби с разными знаменателями к общему знаменателю (смотрите правило и примеры приведения дробей к общему знаменателю). В качестве общего знаменателя возьмем наименьший общий знаменатель, равный НОК(12, 16)=48 . Тогда дополнительным множителем дроби 5/12 будет число 48_12=4 , а дополнительным множителем дроби 9/16 будет число 48_16=3 . Получаем и .

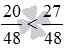
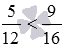
Сравнив полученные дроби, имеем . Следовательно, дробь 5/12 меньше, чем дробь 9/16 . На этом сравнение дробей с разными знаменателями завершено.

.

Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом.

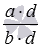
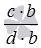
Для сравнения дробей a/b и c/d , их можно привести к общему знаменателю b·d , равному произведению знаменателей сравниваемых дробей. В этом случае дополнительными множителями дробей a/b и c/d являются числа d и b соответственно, а исходные дроби приводятся к дробям и с общим знаменателем b·d . Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b и c/d свелось к сравнению произведений a·d и c·b .

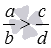
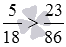
Отсюда вытекает следующее правило сравнения дробей с разными знаменателями: если a·d>b·c , то , а если a·d 414 , то дробь 5/18 больше, чем дробь 23/86 .

.

Сравнение дробей с одинаковыми числителями

Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.

Существует такое правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.

Рассмотрим решение примера.

Сравните дроби 54/19 и 54/31 .

Так как числители сравниваемых дробей равны, а знаменатель 19 дроби 54/19 меньше знаменателя 31 дроби 54/31 , то 54/19 больше 54/31 .

.

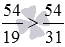
В заключение этого пункта приведем пример, хорошо иллюстрирующий основную суть озвученного правила сравнения дробей с одинаковыми числителями. Пусть перед нами две тарелки, на одной из них 1/2 пирога, а на другой 1/16 этого же пирога. Понятно, что скушав половину пирога, мы будем куда больше сыты, чем съев 1/16 его часть.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом сводится к сравнению двух дробей, если число записать в виде дроби со знаменателем 1 (смотрите натуральное число как дробь со знаменателем 1). Рассмотрим решение примера.

Сравните дробь 63/8 и число 9 .

Число 9 можно представить как дробь 9/1 , этим сравнение дроби 63/8 и числа 9 сводится к сравнению дробей 63/8 и 9/1 . После их приведения к общему знаменателю 8 , получаем дроби с одинаковым знаменателем 63/8 и 72/8 . Так как 63 Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Произвести сравнение заданных дробей 65 126 и 87 126 .

Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

• найти общий знаменатель;
• сравнить дроби.

Рассмотрим данные действия на примере.

Произвести сравнение дробей 5 12 и 9 16 .

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .

Ответ: 5 12 9 16 .

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.

Произвести сравнение дробей 5 18 и 23 86 .

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.

Необходимо выполнить сравнение 63 8 и 9 .

Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 72 , тогда получаем 63 8 72 8 . Значит, заданная дробь меньше целого числа 9 , то есть имеем 63 8 9 .

Мастер-класс: «ХИТРЫЕ» СПОСОБЫ СРАВНЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Курс повышения квалификации за 340 рублей!

Эмоциональное выгорание педагогов. Профилактика и способы преодоления

Муниципальное бюджетное общеобразовательное «Лицей №4» г.о.Коломна

Конспект мастер — класса

тема

«ХИТРЫЕ» СПОСОБЫ СРАВНЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

Заместитель директора по УВР, учитель математики I категории

Ташпулатова Ноила Разимовна

Цели: 1. Формировать способности к построению и использованию

алгоритма сравнения обыкновенных дробей: а) способом

дополнения до 1; б) способом сравнения с промежуточным

Повторить и закрепить: приведение дробей к наименьшему общему числителю, знаменателю, сравнение дробей с одинаковыми числителями и знаменателями, алгоритм сравнения правильных и неправильных дробей, сокращение дробей.

Тип урока: «Открытие» нового знания.

Эпиграф: « Единственный путь, ведущий к

Ход урока: 1.Организационный момент.

Здравствуйте, уважаемые коллеги! Я рада видеть Вас на своём мастер —

классе и надеюсь на взаимное сотрудничество, которое верю, доставит

удовольствие, как мне, так и Вам.

2. Актуализация знаний.

— Открыли тетради, записали число, классная работа.

— запишите их в порядке возрастания

— Каким способом сравнения Вы воспользовались?

— Какие дроби надо прибавить к каждой из этих дробей, чтобы в сумме

получилась единица?

— Какими по отношению к единице являются все использованные нами

— А как из этих дробей получить неправильные?

— Какими они будут по сравнению с 1?

— Сформулируйте правило сравнения правильных и неправильных дробей.

— Приведите дроби последнего ряда к наименьшему общему знаменателю и

запишите их в порядке убывания.

— Сформулируйте правило сравнения, которое Вы применили в этом случае.

— Какая из этих дробей будет лежать на числовом луче правее всех, какая –

— Сформулируйте правило сравнения дробей с помощью числового луча.

Итак, какие способы сравнения обыкновенных дробей мы с Вами повторили?

( Фиксирую на античном сосуде названные способы сравнения).

3. Постановка учебной задачи.

— Сравните дроби и дайте объяснение полученному результату:

( Выполняют задание индивидуально в тетрадях в течение 3 – 4 минут).

По истечении времени проверяем выполненную работу с проговариванием способа сравнения.

— На какой паре дробей возникло затруднение и почему?

— Так какая же возникла перед нами задача?

— А как бы Вы сформулировали тему нашего урока?

Из предложенных вариантов выбираем, подходящее и записываем в тетрадях.

(Возможные варианты: Дополнительные, «хитрые», новые и т.д.

способы сравнения обыкновенных дробей.)

— Повторите ещё раз поставленную на сегодняшний урок задачу.

4. «Открытие» нового знания.

— Чтобы проверить, насколько Вы оказались правы в своих предположениях в 3 и 4 примерах, Вам предлагается выполнить следующие задания:

— представьте частные 8 : 12; 12 : 16; 16 : 20; 20 : 24 в виде несократимых дробей.

— Что интересного Вы заметили в полученном ряду дробей?

— Назовите следующие три дроби.

— Какая дробь стоит на 34 месте? А на 999?

— Предположите, в каком порядке расположены дроби в этом ряду и почему?

— Тогда какой знак сравнения Вы бы поставили между дробями ?

— А как обосновать высказанное предположение?

— Дополните каждую из дробей до 1.

— А легко ли сравнить полученные сравнения?

— Верно, ли было наше предположение в отношении дробей

— А легко ли теперь сравнить дроби из пункта в)?

— Как Вы назвали полученный нами способ сравнения?

— Проговорите ещё раз суть способа сравнения дробей дополнением до 1.

— А можно ли, используя способ дополнения до 1, сравнить дроби

— А может у кого-то из Вас есть гипотеза как это сделать или предположение, в каком направлении нам следует двигаться?

— Тогда я предлагаю Вам поработать в парах над следующим заданием, которое я надеюсь, поможет найти выход из этого затруднительного положения.

— У Вас на партах лежат рисунки, по которым Вам надо:

1. Записать изображённые на рисунках дроби.

2. Составить из них все возможные неравенства.

3. Результат работы представить на доске под соответствующим рисунком.

( Раздаются 4 вида карточек). (Приложение 1)

— Что общего Вы заметили в представленных сравнениях? (1/2).

— Проанализируйте их и сделайте вывод, с каким числом и как Вам приходилось сравнивать?

— А теперь проверьте верно, или неверно было выполнено Ваше сравнение последней пары дробей и объясните почему?

— Какое название данному способу сравнения Вы бы дали?

— Ещё раз сформулируйте суть способа сравнения дробей с ½.

— Более общее название этого способа – это сравнение дробей с промежуточным числом, которое может быть как дробным, так и целым, если мы имеем дело с неправильными дробями.

— Итак, какие новые способы сравнения обыкновенных дробей мы можем применять при решении задач на сравнение?

( Проговаривают названия, а учитель закрепляет их названия на сосуде.)

5. Первичное закрепление во внешней речи.

Выполняют задания карточки №1 «цепочкой» с проговариванием использованного способа сравнения.

КАРТОЧКА № 1 КАРТОЧКА № 1 (Ответы)

(Закрепление полученных знаний) (Закрепление полученных знаний0

Сравните дроби и определите 1.Сравните дроби и определите

способ сравнения: способ сравнения:

и › (по знаменателю)

и ‹ ( сравнение с ½)

и ‹ (сравнение с 1)

и ‹ (приведение к О.З.)

и › ( по числителю)

и ‹ (по дополн. до 1)

и ‹ ( приведение к О.Ч.)

и › (ср с промеж.чис.)

6. Самостоятельная работа с самопроверкой в классе ( 5 минут).

Выполняют задания карточки № 2.

(Самостоятельная работа с самопроверкой)

Сравните дроби наиболее «удобным»

Источник