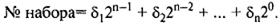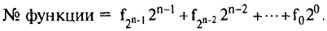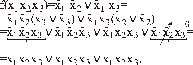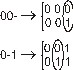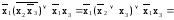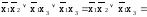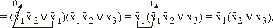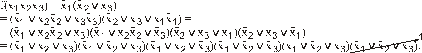Переключательные функции способы задания переключательных функций

Двоичные переключательные функции и способы их задания

Функция f, зависящая от n переменных, называется двоичной переключательной (булевой ), если она и любой из ее аргументов xi, 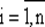принимают значение только из конечного множества, содержащего два элемента.

Таким множеством может быть бинарное множество В = <0, 1>.

Произвольная переключательная функция задается одним из способов: матричным (табличным), геометрическим, аналитическим.

При матричном способе переключательная функция f(x1, . хn) задается таблицей ее значений — таблицей истинности — одномерной или двухмерной (картой Карно), где указываются наборы переменных и соответствующие значения функции.

Под двоичным набором δ = á δ1, δ2, …, δnñ , δ ∈ <0, 1>понимается совокупность значений аргументов x 1, x 2, …, xnПФ.

Иногда двоичные наборы в таблицах истинности удобно представлять номерами наборов:

Значения функций на 2n-наборах также могут быть заданы десятичным номером:

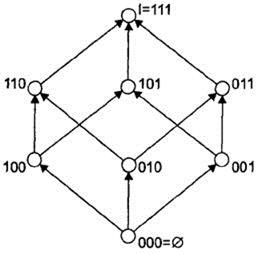
При геометрическом способе ПФ задается с помощью соответствующей отметки вершин n-мерного куба, который по сути является решеткой Хассэ, представляющей собой частично упорядоченное множество наборов (каждая вершина — точка n -мерного пространства). Каждый путь из вершины, соответствующей нулевому набору в вершину единичного набора, соответствует увеличению сравнимых наборов (рис. 28, отношение ≥).

Рис. 28. Геометрическое представление переключательной функции

Этот рисунок изображает частично упорядоченное множество наборов 000, 001, 010, 011, 100, 101, 110, 111, на которых задана переключательная функция трех переменных, например, а, b , с. Вершины, на которых функция равна 1, должны быть как-то отмечены.

Переключательная функция может быть задана и некоторым словесным описанием, указывающим, на каких наборах аргументов какое значение она принимает, и исключающим неверное толкование, всякую двусмысленность. Переключательная функция может быть задана перечислением ее рабочих (единичных), запрещенных (нулевых) и условных наборов (на этих наборах функция не определена). Для упорядоченного задания n -мерных наборов переменных функции f (x 1, x 2, …, xn) удобно рассматривать их в виде целого неотрицательного числа. При этом младший разряд располагается справа. Например, для переменных х5, x 4, х3, х2, х1конкретное их значение истинности 1, 0, 0, 1, 1 соответствует двоичному числу 10011. Это число еще называют номером набора . Для компактной записи наборов значений переменных логической функции целесообразно представлять их номерами — числами в десятичной, восьмеричной, шестнадцатеричной системах счисления. Такой номер-набор называют еще весовым состоянием , или весом этого набора.

Так, 100112↔ 1910↔ 238↔ 1316, ↔ знак эквивалентности.

В случае использования десятичной системы счисления каждой переменной соответствует степень числа 2 (вес разряда) в зависимости от номера переменной, например, в порядке 2423222120. Зафиксированный порядок переменных, каждая из которых имеет свой вес, называется базой функции (старший вес — слева). Переключательная функция может быть задана таблицей истинности, которая иногда еще называется таблицей соответствия.

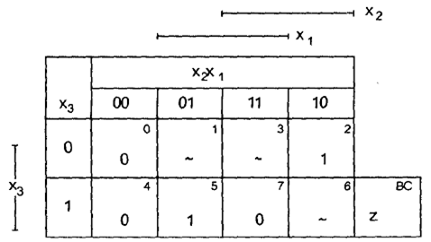
Таблицу истинности можно представить в двухмерном виде, который называется картой Карно (табл. 13–14).

Около карты Карно (табл. 14) иногда указываются области единичного значения переменных. Каждая клетка такой таблицы соответствует одному набору значений переменных, весовое состояние которого указано в правом верхнем углу, и в ней проставлено значение функции на таком наборе.

Таблица 13

Одномерная таблица истинности некоторой функции

Таблица 14

Двухмерная таблица истинности

Переключательная функция может быть представлена в виде формулы, такое представление носит название аналитического. Например, переключательная функция, заданная табл. 13–14, может быть представлена формулой 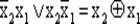, т. е. данная функция не зависит от х3.

Дата добавления: 2016-02-24 ; просмотров: 1487 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Способы задания переключательных функций

Задать переключательную функцию (ПФ) – значит указать ее значение при всех возможных наборах ее аргументов. Логические функции в общем случае могут иметь различные формы представления: словесное, табличное, алгебраическое, графическое (например, карта Карно).

а) табличный способ задания ПФ

Самым простым и наглядным является табличный способ, в котором составляется таблица с указанием всех наборов аргументов и значений функций для них.

Эта таблица называется таблицей истинности или таблицей соответствия.

Кроме наглядности табличный способ обладает тем достоинством, что каждой функции соответствует одна и только одна таблица истинности. Недостаток табл. способа – громоздкость таблицы истинности, растет с возрастанием числа переменных: n=6, 2 6 строк.

Кроме того, эта форма не позволяет выяснить каким образом следует реализовать и можно ли упростить данную функцию.

б) аналитический способ (алгебраический)

Для реализации и последнего упрощения ПФ, их следует представить в аналитической форме, т.е. в принципе можно представить различными аналитическим выражениями. Доказано, что применительно к основному функциональному полному набору (содержащему конъюнкцию, дизъюнкцию и инверсию) любая ПФ, предварительно заданная в табличном виде может быть записана аналитически в двух формах, называемых каноническими (нормальными):

ДСНФ (дизъюнктивная совершенная нормальная форма)

КСНФ (конъюнктивная совершенная нормальная форма)

Аналитическая запись ПФ в ДСНФ и КСНФ строится по средствам суперпозиции (наложения) специальных вспомогательных функций (минтермов m_i и макстермов М_i)

Минтерм – (констентуента единицы) – булево произведение (конъюнкция) от n переменных, в котором каждая переменная входит только один раз, либо в ПК (если ее значение в данном наборе равно 1), либо в инверсном (если значение переменной в наборе равно 0)

Макстерм М_i – (констентуэнта нуля) – булева сумма (дизъюнкция) от n переменных, в который каждая переменная входит только 1 раз в прямом или инверсном виде.

Число макстермов и минтермов равно числу аргументов, на которых функция определена.

Таким образом алгебраическое выражение для любой переключательной функции можно представить в форме:

В принципе обе формы эквивалентны. Выбор формы представления зависит от числа наборов, на которых функция равна 1, либо равна 0.

Где больше 1 – ДСНФ

Где больше 0 – КСНФ.

Однако при минимизации ПФ более удобной является ДСНФ.

в) при относительно небольшом числе элементов (не более 6) в ряде случаев удобным и наглядным является графическое представление ПФ в виде т.н. карт минтермов.

Наиболее распространенная форма – карта Карно.

Карта Карно содержит 2 n клеток, каждая из клеток соответствует одному из минтермов. (q=2 n )

Если требуется представить на карте Карно (кК) функцию, заданную в виде ДСНФ, то в клетках карты для минтермов, входящих в ДСНФ ставится 1, иначе – 0 или оставляются незаполненными.

Существует целый класс, значение которых определено для части наборов аргументов (они называется частично определенные ПФ)

Наборы, для которых ПФ определена – рабочие.

Наборы, для которых ПФ неопределенна – безразличные (в табл. обозначены крестиком). На практике безразличные режимы не реализуются.

Упрощение (минимизация) ПФ

Чем проще логическое выражение для ПФ, тем меньше элементов требуется для ее технической реализации.

Под минимизацией ПФ подразумевают нахождение для нее такой ДНФ, которая имеет минимальную цену или сложность.

Общие методы решения задачи минимизации денежной стоимости цифровых устройств отсутствуют. Наиболее часто процесс минимизации(м.) рассматривается в упрощенной постановке, как поиск дизъюнктивных форм ПФ, содержащих наименьшее число переменных.

Методы минимизации ПФ.

В настоящее время известен целый ряд методов м. в ПФ. Все они основаны на преобразовании логических выражений и подразделяются на систематические и несистематические.

а) систематические методы

Достоинство – их полная формализация, т.е. они описываются строгими алгоритмами. Многие из них реализованы в виде стандартных программ для ЭВМ К числу наиболее распространенных систематических методов относится метод Квайн-Маккласки.

Нахождение минимальной формы производится в 3 этапа:

анализируется вид задания ПФ

Если она задана произвольной формой в булевой алгебре, то с помощью законов алгебры логики она приводится в ДСНФ.

2. нахождение сокращенной ДСНФ с использованием операций склеивания и поглащения. Если в формуле ПФ присутствуют минтермы, отличные друг от друга формой вхождения только одной переменной, то такие минтермы называются смежными (соседними)

Смежные минтермы могут быть попарно склеенными. Результат склеивания – это имбликата, которая представляет собой конъюнкцию, число аргументов в которой на 1 меньше, чем в исходном минтерме.

Обычно в процессе м. склеивают смежные минтермы, затем – имбликаты. Процесс длится до получения имбликат, которые не склеиваются между собой. Такие имбликаты называются простыми, состоящими из дизъюнкции простых импликат, называемых сокращенной ДНФ.

Может показаться, что в сокращенную ДНФ входят имбликаты, наличие или отсутствие которых не сказывается на значение функции. Такие простые имбликаты – избыточные. Если в сокращенной ДНФ удалить все избыточные имбликаты, то получают тупиковую ДНФ.

Искомая минимальная ДНФ совпадает с той из тупиковой, которая содержит наименьшее число вхождений аргументов.

(Метод Квайна Мак Класки – при большом числе переменных, >6. При n≤6 наиболее простым является метод Вейч-Карно, основанный на табличном представлении ПФ.

Карты Карно (диаграмма Вейча) – это прямоугольные таблицы, состоящие из 2 n клеток.

Для задания ПФ надо в каждую клетку занести значение функции, которое она принимает на соответствующем наборе аргументов.

Клетки, содержащие 1 (единица-клетка) –соответствует определенному минтерму. Если в соседних клетках содержится 1, то надо объединить соответствующие минтермы в имбликаты. Такое объединение клеток эквивалентно операции склеивания минтермов, получается более простое выражение для ПФ.

Объединенные клетки будут соответствовать имбликатам, дизъюнкции которых содержат сокращенную ДСНФ:

В прошедшем столетии были сделаны многие открытия и изобретения, сыгравшие революционную роль в развитии современной цивилизации.

создание и развитие средств связи, особенно беспроводной.

Возникновение и развитие авиации и космической техники. Современные летательные аппараты по своим техническим и конструктивным характеристикам не сопоставимы с первыми летательными аппаратами.

Но наиболее разительный прогресс произошел в области вычислительной техники. (ок 50 лет назад первые ЭВМ имели вез ок. 30 тонн, площадь ок. 200м 2 )

время выполнения вычислений измерялось часами или сутками.

Теперь ЭВМ можно разместить на кремниевом кристалле S=5мм 2 , время выполнения расчетов – микросекунды, стоят мало.

При этом в отличие от 1ых ЭВМ, которые программируют в математических кодах и способны были выполнять главным образом только громоздкие математические вычисления, то современные ЭВМ способны доказывать теоремы, переводить текст, воспроизводить движущиеся объекты.

Появление первой машины для выполнения четырех арифметических действий дотируется началом 17 в. (1623 г В. Шикард изобрел мех. машину сложения, вычитания, частично умножения и деления), но более известным оказался настольный арифмометр (1642г.) франц. ученым Паскалем. 1671г. Лейбниц изобрел т.н. зубчатое колесо Лейбница, позволяющее выполнять 4 арифметические операции.

В 19 в. обострилась потребность в выполнении вычислении, связанных с обработкой результатов астрономических наблюдений, расчеты, связанные с составление математических таблиц. Поэтому в 1823 англ. математик Чарльз Бэббидж начал разрабатывать автоматизированную разностную машину, приводимую в действие паровым двигателем.

Машина должна была вычислять значения полиномов и печатать результаты на негативе для фотопечати, однако существующее в то время технические средства не дали возможности завершить воплощение этой идеи, а кроме того, сам Бэббидж увлекся проектированием более мощной счетной машины. Новая счетная машина Бэббиджа получила название «аналитическая».

Источник

26.27. Формы представления переключательных функций. Сднф. Скнф

Одним из способов задания переключательных функций является их представление в виде аналитических выражений (формул). Существуют дизъюнктивная, конъюнктивная и смешанная (скобочная) формы.

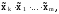
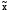
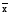
Рассмотрим дизъюнктивные формы представления переключательных функций. Выражение вида содержащее множество попарно различных переменных или их инверсий, называется элементарной конъюнкцией (ЭК). Подпонимается либо сама переменная х, либо ее инверсия.

Если логическая функция, зависящая от n переменных, записана в виде дизъюнкции элементарных конъюнкций ЭК₁ЭК₂. ЭК_r и хотя бы одна ЭК не содержит все n переменных, то такая форма задания называется дизъюнктивной нормальной формой (ДНФ). ДНФ – дизъюнкция конечного множества попарно различных элементарных конъюнкций.

Например: f(аbсd)=а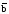bd.

Произвольная функция, например, так называемая скобочная форма, может быть приведена к ДНФ следующим образом:

выполнить все операции инверсии, применяемые к логическим выражениям (группе переменных);

раскрыть все скобки;

в полученном выражении произвести все упрощения.

f(х₁х₂х₃)==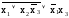

===

==.

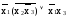
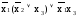
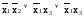
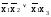
Если все элементарные конъюнкции, входящие в ДНФ, содержат все n переменных, от которых зависит функция, то такая форма называется совершенной дизъюнктивной нормальной формой (СДНФ). СДНФ может быть получена по рабочим (единичным) наборам функций, например по таблице истинности, и наоборот, если задана СДНФ, можно получить таблицу истинности. Однако, если не оговорены условные наборы, все остальные наборы, кроме наборов, соответствующих членам СДНФ, будут считаться запрещенными.

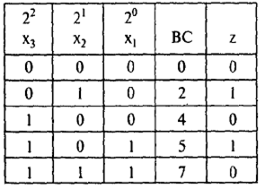
Пусть задана таблица истинности функции сложения по модулю 2 () (табл. 32).

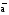
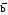
Тогда z(аb)= bа, т.е. это СДНФ.

Первый член СДНФ соответствует строке 01, второй – строке 10.

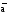
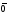
Элементарные конъюнкции, входящие в СДНФ функции, называются конституентами единицы (или минтермами). Конституента единицы обращается в 1 (истинна) на единственном наборе значений переменных. Так, подстановка входного набора 01 (база аb) обращает в 1 конституенту b (1=1). Если считать выражениеz(аb) уравнением, то наборы 01, 10 – его решения.

От СДНФ легко перейти к номерам рабочих наборов в различных системах. Так: z(аb)01₂10₂1₁₀2₁₀.

Аналогично по СДНФ можно получить рабочие наборы, считая остальные запрещенными: z(аb)=1,2[0,3].

Получили символическую форму задания логической функции в десятичных номерах рабочих и запрещенных наборов. Очевидно, не составляет труда и обратный переход – от символической формы, от номеров наборов – к СДНФ.

Для преобразования ДНФ в СДНФ можно выполнить конъюнкцию каждой элементарной конъюнкции, не содержащую i-ю переменную, с тождественно истинным выражением . Таких переменных может быть несколько, будет несколько и тождественно истинных выражений. После этого раскрываются скобки и производятся необходимые упрощения.

Имеется способ получения СДНФ из ДНФ с использованием обобщенного кода, в котором для обозначения недостающих переменных в соответствующих позициях используются знаки «–» (или «

» – «тильда»), а для остальных – символы 0,1.

Функцию 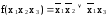представим в виде: 00-0-1.

Тогда, подставляя вместо «–» всевозможные комбинации 0,1, получим:

Таким образом, получили номера 000, 001, 011, которые соответствуют членам СДНФ.

СДНФ переключательной функции, тождественно равной 1 (тождественно истинной), содержит 2 n констинтуэнт (n – число переменных).

Переключательная функция может быть представлена в конъюнктивной форме.

Выражение вида 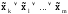, содержащее множество попарно различных переменных или их инверсий, называется элементарной дизъюнкцией (ЭД).

Если переключательная функция, зависящая от n переменных, записана в виде конъюнкции элементарных дизъюнкций ЭД₁·ЭД₂·. ·ЭД_r и хотя бы одна ЭД не содержит все n переменных, то такая форма задания называется конъюнктивной нормальной формой (КНФ). КНФ – конъюнкция конечного множества попарно различных элементарных дизъюнкций.

Например: f(аbсd)=а(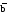с)(bd).

Произвольная функция, например, скобочная форма, может быть всегда приведена к КНФ следующим образом:

заданную функцию инверсировать, получить ДНФ инверсной функции;

ДНФ инверсной функции инверсировать еще раз, получить тождественную исходной функцию в КНФ;

на каждом этапе следует производить необходимые упрощения.

f(х₁х₂х₃)=;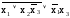

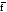
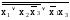
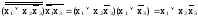
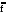
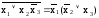
(х₁х₂х₃)==

=;

(х₁х₂х₃)=.

Второй способ получения КНФ заключается в выполнении всех операций инверсии, применяемой к группе переменных (логическим выраженииям), затем используется распределительных закон.

f(х₁х₂х₃)=

=

=

Если все элементарные дизъюнкции, входящие в КНФ, содержат все n переменных, от которых зависит функция, то такая форма называется совершенной конъюнктивной нормальной (СКНФ).

СКНФ может быть получена по запрещенным (нулевым) наборам функции, например по таблице истинности. Для получения СКНФ по таблице истинности необходимо составить элементарные дизъюнкции всех переменных для каждой строки таблицы, в которой функция равна 0. При этом в дизъюнкцию входит сама переменная, если ее значение равно 0, и отрицание переменной, если ее значение равно 1.

Так, для функции сложения по модулю 2 (табл. 32) СКНФ имеет вид:

.

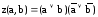
Элементарные дизъюнкции, входящие в СКНФ функции, называются конституентами нуля (макстермами).

Конституента нуля обращается в нуль на единственном наборе переменных, который является запрещенным (нулевым) набором функции. Например, для функции сложения по модулю 2 конституента нуля (аb) обращается в 0 на наборе 00, а конституента нуля 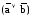– на наборе 11.

От СКНФ можно перейти к номерам запрещенных наборов в различных системах счисления. Для получения двоичных номеров в порядке базы функции (например, аb) необходимо заменить символы переменных с инверсией на 1, а без инверсии – на 0 и записать вместо элементарных дизъюнкций соответствующие совокупности двоичных чисел.

Если дополнительной информации нет, то все остальные числа из области задания функции считаются рабочими.

Для преобразования КНФ в СКНФ можно выполнить дизъюнкцию каждой элементарной дизъюнкции, не содержащей i-ю переменную, с тождественно ложным выражением 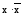. Таких недостающих переменных может быть несколько; тогда надо добавлять соответствующие тождественно истинные выражения. Затем применяется распределительный закон и производятся необходимые упрощения.

Соответствующие запрещенные наборы: 100, 110, 101, 111, 010 (база х₁х₂х₃).

Получим СДНФ и СКНФ ПФ, заданной десятичным номером №174₁₀.

Таблица истинности ПФ №174₁₀ показана в табл. 33

Источник