- Перпендикуляр к прямой
- Теорема
- Проведение перпендикуляра из точки к прямой
- Переформируйте описание способа проведения перпендикуляра
- Теорема о перпендикулярных прямых
- Свойство перпендикулярных прямых
- Интересное по рубрике
- Найдите необходимую статью по тегам
- Подпишитесь на нашу рассылку
- Мы в инстаграм
- Рекомендуем прочитать
- Реальный опыт семейного обучения
- Учитель информатики
- Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
- ГДЗ по Информатике 11 класс. Основные сведения об алгоритмах.
Перпендикуляр к прямой
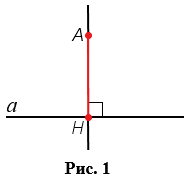
Возьмем прямую 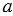
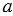
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой 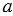
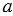
Теорема
| Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. |
Доказательство:
1. Существование перпендикуляра.
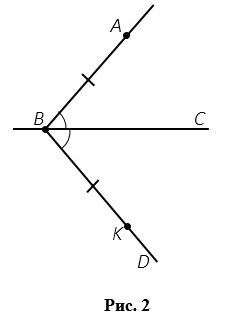
Пусть точка А не лежит на прямой ВС. Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (Рис.2).
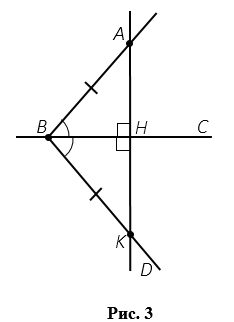
Проведем прямую АК, пусть Н — точка пересечения прямых ВС и АК (Рис.3).
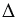
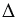










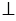
2. Единственность перпендикуляра.
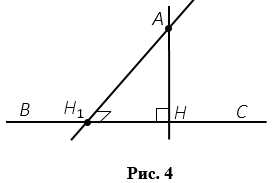
Предположим, что через точку А можно провести еще один перпендикуляр АН1 к прямой ВС, тогда получим, что две прямые АН и АН1, перпендикулярные к прямой ВС пересекаются в точке А (Рис.4). Но по свойству перпендикулярных прямых, прямые АН и АН1 пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.
Проведение перпендикуляра из точки к прямой
Для проведения перпендикуляра из точки к прямой, используют чертежный угольник (Рис.5). Чертежный угольник прикладывают так, чтобы одна из его сторон, образующих прямой угол угольника, располагалась вдоль прямой, к которой нужно провести перпендикуляр. Вдоль второй стороны, образующей прямой угол угольника, проводим прямую так, чтобы она проходила через точку, из которой нужно провести перпендикуляр к прямой. Отрезок, соединяющий точку на прямой, к которой нужно провести перпендикуляр, и точку, из которой нужно провести перпендикуляр, и есть перпендикуляр проведенный из данной точки к данной прямой. На Рис.5 АН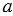
Поделись с друзьями в социальных сетях:
Источник
Переформируйте описание способа проведения перпендикуляра
Углы бывают острые, прямые и тупые.
Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.
Два угла с одной общей стороной называются смежными.
На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.
Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°
При пересечении двух прямых образуются четыре угла:
Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.
∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4
То же справедливо и для ∡1 и ∡3.
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.
∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.
Перпендикулярность прямых принято обозначать так: a⟂b
Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!
Теорема о перпендикулярных прямых
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.
Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.
Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.
Свойство перпендикулярных прямых
Две прямые, перпендикулярные третьей, не пересекаются.
Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Интересное по рубрике
Найдите необходимую статью по тегам
Подпишитесь на нашу рассылку
Мы в инстаграм
Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Рекомендуем прочитать
Реальный опыт семейного обучения
Звонок по России бесплатный
Пишите нам письма
Посмотреть на карте
Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.
Источник
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
ГДЗ по Информатике 11 класс. Основные сведения об алгоритмах.
§ 5. Основные сведения об алгоритмах
Придумайте систему команд исполнителя Колдун. Запишите с их помощью план действий исполнителя по приготовлению эликсира.
Сколько разных алгоритмов, состоящих из пяти команд, можно составить для этого исполнителя? Сколько из них будут приводить к одинаковым результатам для заданного числа х?
9. Исполнитель Автомат получает на вход четырёхзначное число. Это число он преобразует по следующему алгоритму:
1) вычисляется сумма первой и второй цифр числа;
2) вычисляется сумма второй и третьей цифр числа;
3) вычисляется сумма третьей и четвёртой цифр числа;
4) из полученных трёх чисел (сумм) выбирается и отбрасывается одно — не превышающее двух других чисел;
5) оставшиеся два числа записываются друг за другом в порядке неубывания без разделителей.
Так, если исходное число 9575, то, преобразуя его, автомат создаст суммы: 9 + 5 = 14, 5 + 7 = 12, 7 + 5 = 12. Сумма, не превышающая двух других, 12. Оставшиеся суммы: 14, 12. Результат: 1214.
Опишите систему команд этого исполнителя.
Могут ли результатом работы этого исполнителя быть числа 1610, 1010, 1019?
Укажите минимальное и максимальное значения результата работы этого исполнителя.
При обработке некоторого числа х автомат выдаёт результат 1418. Укажите наименьшее и наибольшее значения х, при которых возможен такой результат.
Источник

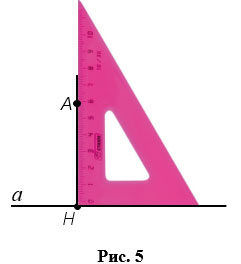
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)














