Перечислительный способ задания множества

02. Способы задания множеств

Существуют два основных способа задания множеств:

1. Перечислительный способ (перечисление элементов)

2. Высказывательный способ (описание свойств элемента).

Перечислительный Способ состоит в составлении полного списка элементов множества, заключенного в фигурные скобки и применяется только для конечных множеств с небольшим числом элементов. Множество записывается в следующей форме:

Высказывательный Способ состоит в задании такого свойства, наличие которого у элементов определенного множества является истиной. Описание свойства элементов обычно задается так: пусть

Р(х) — утверждение, заключающееся в том, что элемент х обладает свойством Р. Тогда запись

Х = <X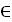M | Р(х)>

Означает, что рассматриваемое множество Х состоит из элементов некоторого множества М, обладающих свойством Р.

Пример. Запись А=<X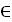R| (X2+2X-15=0)> означает, что множество A состоит из действительных корней уравнения: X2+2X-15=0. Это же множество можно также задать перечислительным способом: A=<-5,3>.

Конечное множество может быть задано обоими способами, а бесконечные – лишь высказывательным способом. Пустые множества относятся к конечным.

Если рассматривать теорию множеств без ограничений на способы задания множеств, то такая теория называется Наивной теорией множеств.

Еще при жизни Г. Кантора, создателя наивной теории множеств, были обнаружены многочисленные парадоксы в этой теории.

Приведем один из известных парадоксов Б. Рассела.

Пусть М — множество всех множеств. Тогда очевидно, что М ϵ М. Тем самым, существуют множества, содержащие себя как свой элемент.

Рассмотрим некоторое множество X, которое не содержит себя как свой элемент.

Пусть Y — множество всех таких множеств X, т. е. множество всех множеств, не содержащих себя как свой элемент.

Зададимся вопросом: каково множество Y? Содержит оно себя как элемент или нет? Возможны два случая: 1) содержит; 2) не содержит.

В первом случае YϵY. Тогда по определению множества Y имеем Y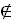Y. Получили противоречие.

Во втором случае Y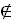Y. Тогда по определению множества Y имеем YϵY. Получили также противоречие.

Иногда этот парадокс Рассела облекают в бытовую форму. Тогда появляется следующая парадоксальная ситуация. В полку имеется полковой Брадобрей, который руководствуется следующим приказом. Брить бороды только у тех людей, которые сами себя не бреют. Спрашивается, может ли Брадобрей брить себе бороду? Получается так, что если он не бреет себе бороду, то по приказу он должен себя брить. Как только Брадобрей начинает брить себе бороду, то по приказу он не должен себя брить. Парадокс.

Избежать парадоксов удается только в рамках аксиоматической теории множеств, т. е. теории, которая ограничивает способы задания множеств специальной аксиоматикой.

Источник

1.2 Способы задания множеств

Существуют два основных способа задания множеств:

Перечислительный способ (перечисление элементов)

Высказывательный способ (описание свойств элемента).

Перечислительный способ состоит в составлении полного списка элементов множества, заключенного в фигурные скобки и применяется только для конечных множеств с небольшим числом элементов. Множество записывается в следующей форме:

Высказывательный способ состоит в задании такого свойства, наличие которого у элементов определенного множества является истиной. Описание свойства элементов обычно задается так: пусть

Р(х) — утверждение, заключающееся в том, что элемент х обладает свойством Р. Тогда запись

Х = <xM | Р(х)>

означает, что рассматриваемое множество Х состоит из элементов некоторого множества М, обладающих свойством Р.

Пример. Запись А=<xR| (x 2 +2x-15=0)> означает, что множество A состоит из действительных корней уравнения: x 2 +2x-15=0. Это же множество можно также задать перечислительным способом: A=<-5,3>.

Конечное множество может быть задано обоими способами, а бесконечные – лишь высказывательным способом. Пустые множества относятся к конечным.

Если рассматривать теорию множеств без ограничений на способы задания множеств, то такая теория называется наивной теорией множеств.

Еще при жизни Г. Кантора, создателя наивной теории множеств, были обнаружены многочисленные парадоксы в этой теории.

Приведем один из известных парадоксов Б. Рассела.

Пусть М — множество всех множеств. Тогда очевидно, что М ϵ М. Тем самым, существуют множества, содержащие себя как свой элемент.

Рассмотрим некоторое множество X, которое не содержит себя как свой элемент.

Пусть Y — множество всех таких множеств X, т. е. множество всех множеств, не содержащих себя как свой элемент.

Зададимся вопросом: каково множество Y? Содержит оно себя как элемент или нет? Возможны два случая: 1) содержит; 2) не содержит.

В первом случае YϵY. Тогда по определению множества Y имеем Y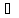Y. Получили противоречие.

Во втором случае YY. Тогда по определению множества Y имеем YϵY. Получили также противоречие.

Иногда этот парадокс Рассела облекают в бытовую форму. Тогда появляется следующая парадоксальная ситуация. В полку имеется полковой Брадобрей, который руководствуется следующим приказом. Брить бороды только у тех людей, которые сами себя не бреют. Спрашивается, может ли Брадобрей брить себе бороду? Получается так, что если он не бреет себе бороду, то по приказу он должен себя брить. Как только Брадобрей начинает брить себе бороду, то по приказу он не должен себя брить. Парадокс.

Избежать парадоксов удается только в рамках аксиоматической теории множеств, т. е. теории, которая ограничивает способы задания множеств специальной аксиоматикой.

Глава 2. Операции над множествами

2.1 Сравнение множеств

Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие.

Два множества равны, если они являются подмножествами друг друга:

А = В = А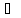В & ВА.

Мощность множества М обозначается как |М|. Для конечных множеств мощ­ность — это число элементов. Например, |0| = 0, но |<0>| = 1. Если |А| = |В|, то множества А и В называются равномощными.

Если множества A и В содержат одни и те же элементы и мощности их равны, то эти множества считаются равными. Это обозначается так: А=В. Неравные множества состоят из различных элементов, обозначается так: А≠В.

Равенство множеств обладает следующими свойствами:

• А = В — рефлексивность;

• если А = В, то В = А — симметричность;

• если А = В и В = С, то А = С — транзитивность.

Отметим, что множества, которые содержат себя в качестве одного из своих элементов, называются экстраординарными. Остальные множества, не относящиеся к ним, называются ординарными.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

—> Детская Энциклопедия —>

Два способа задания множества. Множества и высказывания

Поставим теперь вопрос о том, каким обра­зом можно задать то или иное множество. Про ще всего это сделать, перечислив все элементы, в совокупности составляющие данное множе­ ство: так, можно сказать, что фигурирующее выше множество А состоит из школьников Пе ти, Саши, Кати, Веры и Наташи. Однако в тех случаях, когда множество содержит много эле­ментов, этот явный, или перечислительный, способ задания множества может оказать­ся очень неудобным. Кроме того, при таком за­дании множества обычно оказывается зама­скированным самый принцип его образования, то общее, что служит причиной объединения отобранных элементов в одно множество.

Второй способ задания множества состоит в том, что мы указываем признак, харак­теризующий все элементы множества, и только эти элементы. Так, выше мы говорили: «множе­ство отличников» или «множество уча­щихся, сидящих в классе в пер­вом ряду». Такой способ задания множе­ства называется неявным или описатель­ным. Этот способ заключается в том, что мы фор­мулируем некоторое высказывание, касающееся элементов рассматриваемого уни­версального множества I («быть отлични­ком» или «сидеть в первом ряду»); далее отби­раем те, и только те, элементы множества I, которые этому высказыванию удовлетворяют.

Описательный способ задания множества связывает учение о множествах с учением о высказываниях, составляющим предмет математической логики. Высказы­ванием мы называем всякое утверждение, которое может оказаться истинным или лож­ным; при этом предполагается, что в принципе существует возможность установить, истинно данное высказывание или ложно, хотя мы, быть может, этой возможности не имеем. С этой точ­ки зрения утверждение «ровно через 100 лет в этот. день в Москве будет ясная погода» является высказыванием, поскольку через 100 лет можно будет проверить, правда это или нет. Напротив, утверждение «неделя — это большой промежуток времени» высказыва­нием не является в силу неопределенности выражения «большой промежуток времени», которое у разных лиц и в различных обстоя­тельствах может иметь совершенно разный смысл; здесь, не обладая несколькими допол­нительными сведениями, никак нельзя сказать, является это утверждение истинным или нет.

Рассмотрим теперь высказывания, относя­щиеся к элементам определенного универсаль­ного множества I; в случае, когда этим мно­жеством является множество учащихся дан­ного класса, это могут быть высказывания: «он отличник», «он сидит в первом ряду», «он выше 1 м 50 см», «он старше 50 лет», «он — это девочка», «он левша», «он имеет две головы» и т. д. Каждому такому высказыванию отве­чает некоторое множество элементов из I, для которых это высказывание является истинным; это множество называется множеством истинности данного высказывания. Мно­жество истинности может оказаться пустым; в этом случае высказывание называется тож­дественно ложным или проти­воречивым. Так, для множества учеников данного класса тождественно ложными будут высказывания «он имеет две головы» или «ему больше 50 лет»; выше у нас фигурировало еще одно высказывание, также заведомо противо­речивое в применении к ученикам какого-либо класса: «он слон». В определенном смысле противоположный случай — это тот, когда мно­жество истинности данного высказывания сов­падает со всем универсальным множеством I; в этом случае высказывание называется тож­дественно истинным или бес­содержательным. Тождественно истин­ными являются, например, высказывания: «он (ученик определенного класса) моложе 50 лет», «он мальчик или девочка».

Источник

Способы задания множеств.

ПЛАН

1. Понятие множества.

2. Способы задания множеств.

3. Отношения между множествами.

4. Операции над множествами.

5. Свойства операций над множествами.

6. Понятие «система счисления».

7. Непозиционная система счисления.

8. Позиционная система счисления.

9. Перевод чисел из одной системы счисления в другую.

Понятие множества.

Для сокращенной записи будем использовать следующие символы:

• a Î A — а является элементом множества А;

• a Ï A — а не является элементом множества А;

• — пустое множество;

• <a, d, с> — множество, состоящее из трех элементов a, d и с;

• <х|Р(х)> — множество, состоящее из таких элементов х, для которых истинно утверждение Р(х);

• A È B — объединение множеств A и В;

• A Ç B — пересечение множеств А и В;

• A Ì B — А является подмножеством В;

• — дополнение множества А до универсального множества;

• U — универсальное множество;

• a R b — между a и b существует бинарное отношение R.

Множество является самым широким понятием в математике и поэтому принимается без определения. Множество считается заданным, если относительно каждого объекта можно сказать, принадлежит он данному множеству или нет. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли — всё это примеры множеств.

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

Пустое множество ( ) не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения sin x = 2 и т.д.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Счётное множество — множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке) или бесконечным (множество целых чисел, его элементы можно пронумеровать следующим образом:

элементы множества: . -5, — 4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .

номера элементов: . 11 9 7 5 3 1 2 4 6 8 10 . ).

Несчётное множество — множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным.

Выпуклое множество — множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружность не является выпуклым множеством.

Способы задания множеств.

Если объект a является элементом множества A, то говорят, что a принадлежит A, и записывают a A . Запись a Ï A означает, что a не принадлежит A.

Множество может быть задано следующим образом:

• перечислением всех его элементов по их названиям (так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

Множество можно задать перечислением всех его элементов в любом порядке. Если множество A, например, состоит из первых четырех букв русского алфавита, то записывают

• заданием общей характеристики (общих свойств) элементов данного множества (например, множество рациональных чисел, собаки, семейство кошачьих и т.д.);

Множество может быть задано с помощью характеристического свойства, т.е. такого свойства, которым обладают все элементы данного множества и не обладают никакие другие объекты. Если множество A задано с помощью характеристического свойства P, то записывают A = <x|p(x)>

Например, запись A = <x|x R,—7

N — множество натуральных чисел;

Z — множество целых чисел;

Q — множество рациональных чисел;

R — множество действительных чисел.

Пример 1.1. Запишем различными способами множество A, элементами которого являются натуральные числа, не превосходящие числа 6.

Решение. Натуральными числами, не превосходящими числа 6, являются: 1, 2, 3, 4, 5, 6. Поэтому множество A можно записать так: A = <1, 2, 3, 4, 5, 6>, или A = <1, 3, 5, 2, 4, 6>, или A = <6, 5, 4, 3, 2, 1>, или перечислением элементов в каком-либо другом порядке.

По условию множество A задано описанием характеристического свойства его элементов «Быть натуральным числом, не превосходящим числа 6». Используя это свойство, множество можно записать так: A = <x|x N,x б>.

Пример 1.2. Прочитаем различными способами следующие записи:

а) 37 N ;

Решение. а) Число 37 является натуральным. Число 37 принадлежит множеству N. Число 37 — элемент множества N. Число 37 содержится во множестве N. Множество N содержит число 37.

б) Число 2,5 не является натуральным. Число 2,5 не принадлежит множеству N. Число 2,5 не является элементом множества N. Число 2,5 не содержится во множестве N. Множество N не содержит числа 2,5.

Пример 1.3. Используя понятие характеристического свойства, зададим следующие множества:

Решение. Множества A, B и C заданы способом перечисления элементов. Используя характеристические свойства, указанные множества можно задать следующим образом:

A — множество согласных букв русского алфавита;

B — множество цветов радуги;

C — множество дней недели.

Пример 1.4. Изобразим на числовой прямой элементы следующих множеств:

б) A = <x|x Z,—4 x

Источник