Перечислите способы задания плоскости зарисуйте рисунки

Способы задания плоскости в пространстве

Все возможные способы задания плоскости в пространстве представлены в следующей таблице.

Аксиома о плоскости, заданной тремя точками.

Через три различные точки в пространстве проходит одна и только одна плоскость.

Теорема о плоскости, определяемой прямой и точкой.

Через прямую и точку, не лежащую на этой прямой, проходит одна и только одна плоскость.

Теорема о плоскости, определяемой двумя пересекающимися прямыми.

Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Теорема о плоскости, определяемой двумя параллельными прямыми.

Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Аксиома о плоскости, заданной тремя точками.

Через три различные точки в пространстве проходит одна и только одна плоскость.

Теорема о плоскости, определяемой прямой и точкой.

Через прямую и точку, не лежащую на этой прямой, проходит одна и только одна плоскость.

Теорема о плоскости, определяемой двумя пересекающимися прямыми.

Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Теорема о плоскости, определяемой двумя параллельными прямыми.

Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Утверждение . Через любую прямую в пространстве проходит бесконечно много плоскостей (рис.5).

Замечание . Через любые две скрещивающиеся прямые скрещивающиеся прямые не проходит ни одной плоскости.

Источник

Перечислите способы задания плоскости зарисуйте рисунки

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис. 41 );

Фигура	Рисунок	Тип утверждения и формулировка
Три различные точки
Прямая линия и точка, не лежащая на этой прямой
Две пересекающиеся прямые
Две параллельные прямые
Прямая линия и точка, не лежащая на этой прямой

Рисунок 41. Плоскость, заданная тремя точками, не лежащими на одной прямой

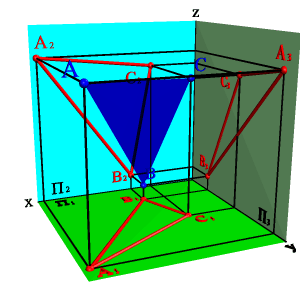
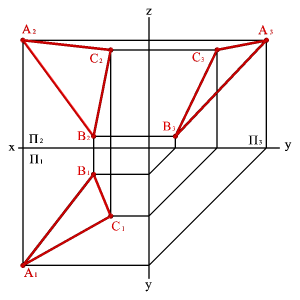
а) модель		б) эпюр

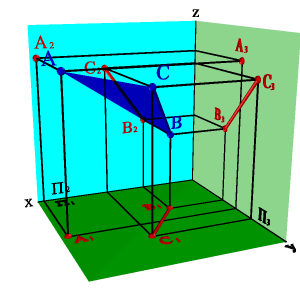
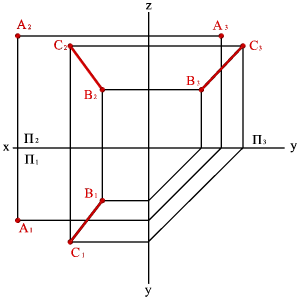
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);

Рисунок 42. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии

а) модель		б) эпюр

3. двумя пересекающимися прямыми (рис.43);

Рисунок 43. Плоскость, заданная двумя пересекающимися прямыми

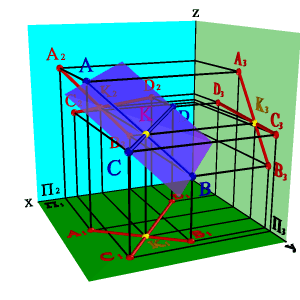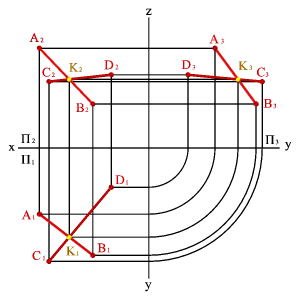а) модель		б) эпюр

4. двумя параллельными прямыми (рис.44);

Рисунок 44. Плоскость, заданная двумя п араллельны ми прямы ми

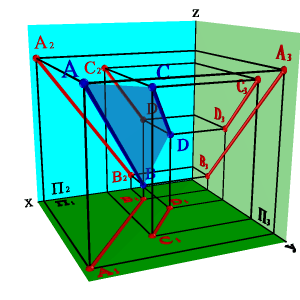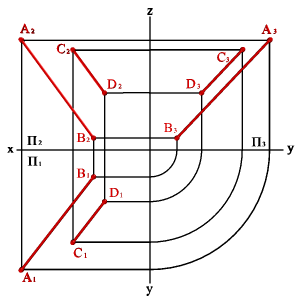а) модель		б) эпюр

5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).

С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a _П1, фронтальный a _П2 и профильный a _П3 следы.

Рисунок 45. Плоскость, заданная следами

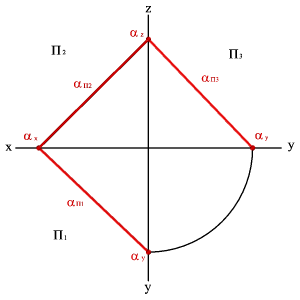а) модель		б) эпюр

Следы плоскости общего положения пересекаются попарно на осях в точках a _x , a _y , a _z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

Источник

Способы задания плоскости. Положение прямой относительно плоскости. Взаимное положение плоскостей

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования «Алтайский государственный технический университет

Бийский технологический институт (филиал)

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ.

ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТИ.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Методические рекомендации по изучению курса начертательной геометрии для студентов специальностей 151001 дневной, вечерней и заочной форм обучения

Куничан, задания плоскости. Положение прямой относительно плоскости. Взаимное положение плоскостей: методические рекомендации по изучению курса начертательной геометрии для студентов специальностей 151001 дневной, вечерней и заочной форм обучения / .

Алт. гос. тех. ун-т, БТИ. — Бийск.

Изд-во Алт. гос. тех. ун-та, 20с.

В методических рекомендациях представлен теоретический материал для изучения тем «Способы задания плоскости. Положение прямой относительно плоскости. Взаимное положение плоскостей».

Рассмотрены и одобрены на заседании
кафедры технической графики.

Протокол № 17 от 01.01.01 г.

Рецензент: к. т.н. доцент каф. МРСиИ (БТИ АлтГТУ)

ã БТИ АлтГТУ, 2007

1 ПЛОСКОСТЬ. СПОСОБЫ ЗАДАНИЯ.

ПРЯМЫЕ И ТОЧКИ ПЛОСКОСТИ

1.1 Способы задания плоскости

На эпюре плоскость может быть задана проекциями геометрических элементов, определяющих ее (рисунок 1.1): проекциями трех точек А, В, С, не лежащих на одной прямой; проекциями прямой EF и точки D вне её; двумя пересекающимися прямыми m, n; двумя параллельными прямыми k, l.

Кроме этого, плоскость может быть задана проекциями любой плоской фигуры — треугольника, квадрата, круга и т. д.

На рисунке 1.1 нетрудно увидеть, что от одной формы задания плоскости путем несложных построений можно перейти к любой другой форме. Так, соединив точки А и В прямой линией, перейдем от способа задания плоскости проекциями трех точек к способу задания плоскости проекциями прямой и точки вне ее и т. д.

Плоскость можно задать следами. На рисунке 1.2 изображена некоторая плоскость Р в системе V, Н, W. Эта плоскость пересекает плоскости проекций по прямым, обозначенным на чертеже PV, PH и PW.

Прямые, по которым некоторая плос-кость Р пересекает плоскости проекций, называются следами этой плоскости:

PV — фронтальный след плоскости Р;

PH — горизонтальный след плоскости Р;

Точки Рх, Pу, Pz — точки пересечения следов плоскости (точки схода следов), лежащие на соответствующих осях.

Следовательно, плоскость на эпюре может быть задана проекциями ее следов.

На рисунке 1.4 дан эпюр плоскости Р, заданной проекциями ее следов, в системе V/H.

Следует иметь в виду, что фронтальная проекция фронтального следа плоскости совпадает с самим следом, а горизонтальная проекция его — с осью X. Аналогично, горизонтальная проекция горизонтального следа совпадает с самим следом, а фронтальная проекция горизонтального следа — с осью X.

Рисунок 1.3 Рисунок 1.4

1.2 Характерные положения плоскости относительно плоскостей

проекций (плоскости частного положения)

По положению плоскостей относительно плоскостей проекций различают следующие:

1. Плоскости, не перпендикулярные и не параллельные ни одной из плоскостей проекций. Это плоскости общего положения (рисунок 1.5). Следы плоскостей общего положения никогда не перпендикулярны к осям проекций.

2. Плоскости, перпендикулярные к одной из плоскостей проекций:

а) плоскости, перпендикулярные к горизонтальной плоскости проекций — это горизонтально проектирующие (проецирующие) плоскости (рисунок 1.6), у которых фронтальный след всегда перпендикулярен к оси X.

Если в горизонтально проектирующей плоскости находится точка или прямая, то их горизонтальные проекции всегда будут находиться на горизонтальном следе плоскости. Угол b (см. рисунок 1.6) – угол между горизонтально проектирующей (проецирующей) плоскостью и плоскостью проекций V;

б) плоскости, перпендикулярные к фронтальной плоскости проекций — это фронтально проектирующие (проецирующие) плоскости (рисунок 1.7), у которых горизонтальный след всегда перпендикулярен к оси X. Если во фронтально проектирующей плоскости находится точка или прямая, то их фронтальные проекции всегда лежат на фронтальном следе плоскости. Угол a (см. рисунок 1.7) — угол между фронтально проектирующей плоскостью и плоскостью проекций Н;

в) плоскости, перпендикулярные к профильной плоскости проекций — это профильно проектирующие (проецирующие) плоскости (рисунки 1.8, 1.9).

3. Плоскости, перпендикулярные к двум плоскостям проекций, — плоскости уровня:

а) плоскости, перпендикулярные к плоскостям V и W, т. е. параллельные плоскости Н, — это горизонтальные плоскости уровня (рисунок 1.10);

б) плоскости, перпендикулярные к плоскостям Н и W, т. е. параллельные плоскости V, — это фронтальные плоскости уровня (рисунок 1.11);

в) плоскости, перпендикулярные к плоскостям Н и V, т. е. параллельные плоскости W, — это профильные плоскости уровня (рисунок 1.12).

1.3 Прямая и точка в плоскости

Возможны следующие три случая относительного расположения прямой и плоскости: прямая принадлежит плоскости, прямая параллельна плоскости, прямая пересекает плоскость.

1.3.1 Принадлежность прямой и точки плоскости

Из элементарной геометрии известно, что прямая принадлежит плоскости, если она:

1) проходит через две точки, принадлежащие данной плоскости;

2) проходит через точку, принадлежащую данной плоскости, и параллельна какой-либо прямой, находящейся в этой плоскости или ей параллельной.

На рисунке 1.13 построены произвольные прямые, принадлежащие плоскости ΔАВС. На рисунке 1.13а прямая 1-2 удовлетворяет первому условию, а на рисунке 1.13б прямая m удовлетворяет второму условию. (Точки 1 и 2 лежат на сторонах треугольника, т. е. заведомо принадлежат ему, а прямая m параллельна стороне ас и проходит через точку b треугольника.)

На рисунках 1.14 и 1.15 построены прямые m и n, принадлежащие плоскостям, заданным следами.

Рисунок 1.14 Рисунок 1.15

Точка принадлежит плоскости, если лежит на прямой, принадлежащей плоскости. Рассмотрим подробнее на примере.

Задача. Постройте произвольный пятиугольник abcde, все точки которого лежат в одной плоскости (рисунок 1.16).

Решение: Точки abc на фронтальной и горизонтальной плоскостях строим произ-вольно (соблюдая только перпендикуляр-ность линий связи). Для построения точки d проводим прямую а-1, которая заведомо принадлежит плоскости треугольника. На ее продолжении произвольно отмечаем точку (т. е. две проекции точки). Для построения точки е произвольно проводим прямую с-2; на ее продолжении отмечаем точку с (т. е. две проекции точки).

1.3.2 Построение следов плоскости

От любого из способов задания плоскости можно перейти к заданию её следами, т. е. построить следы заданной плоскости.

На рисунках 1.17 и 1.18 построены следы плоскостей, заданных двумя параллельными и двумя пересекающимися прямыми. Построения в обоих случаях аналогичны: вначале построены следы прямых и через одноименные следы прямых проведены следы плоскости (так как следы прямых, принадлежащих плоскости, всегда находятся на одноименных следах плоскости).

Рисунок 1.17 Рисунок 1.18

1.3.3 Прямые особого положения в плоскости

К прямым особого положения в плоскости относятся следующие.

Горизонтали плоскости — это прямые, лежащие в данной плоскости и параллельные плоскости проекций Н.

Горизонтальная проекция горизонтали всегда параллельна горизонталь-ному следу плоскости, а фронтальная — параллельна оси X.

На рисунке 1.19 изображены горизонтали плоскостей, заданных
а) следами; б) параллельными прямыми; в) треугольником.

Рисунок 1.19

Фронтали плоскости — это прямые, лежащие в заданной плоскости и параллельные плоскости проекций V.

Фронтальная проекция фронтали всегда параллельна фронтальному следу плоскости, а горизонтальная — параллельна оси X (рисунок 1.20а).

На рисунке 1.20б изображена фронталь плоскости, заданной ΔABC, которая проходит через точки m, n.

На рисунке 1.20в фронталь плоскости, заданной параллельными прямыми, проходит через точку А.

Рисунок 1.20

Линии наибольшего ската плоскости относительно плоскостей Н и V — это прямые, лежащие в заданной плоскости и перпендикулярные к горизонталям и фронталям этой плоскости, в том числе и к её горизонтальному и фронтальному следам.

ВК — линия наибольшего ската плоскости Q к плоскости Н (рисунок 1.21). BК ^ QH, но и bk ^ QH (на основании теоремы о проекциях прямого угла). Значит, угол ВКb — линейный угол двугранного угла, образованного плоскостями Q и Н. Следовательно, линия наибольшего ската плоскости может служить для определения угла наклона этой плоскости к плоскости проек-
ций Н.

Рисунок 1.21

Из рисунка 1.21 видно, что угол наклона линии ската к плоскости проекций равен углу наклона самой плоскости. А это значит, что для того, чтобы найти углы наклона плоскости общего положения к плоскостям проекций, достаточно найти углы наклона линии ската к соответствующим плоскостям проекций. Подробнее это рассмотрено на примере (рисунок 1.24).

На рисунках 1.22 и 1.23 приведено построение линии наибольшего ската ВК в плоскостях, заданных следами (см. рисунок 1.22) и ΔABC (см. рисунок 1.23).

Рисунок 1.22 Рисунок 1.23

Пример. Определить углы наклона ΔАВС к плоскостям H и V.

Решение: Проведите в плоскости ΔАВС горизонталь h. На горизонтальной проекции постройте проекцию линии ската 21-31. По линиям связи постройте ее фронтальную проекцию 22-32. Методом прямоугольного треугольника определите натуральную величину угла α линии ската 21-31. Он соответствует углу наклона всей плоскости ΔАВС к плоскости Н (рисунок 1.24).

Чтобы определить угол наклона ΔАВС к фронтальной плоскости проекций, постройте линию ската на фронтальной плоскости проекций. Для этого проведите фронталь f. На фронтальной плоскости перпендикулярно фронтальной проекции фронтали проведите проекцию линии ската 52-62. Методом прямоугольного треугольника определите натуральную величину угла β линии ската 5-6. Он соответствует углу наклона ΔАВС к плоскости V.

2 ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ

ОТНОСИТЕЛЬНО ДРУГ ДРУГА

Прямая относительно плоскости может занимать следующие положения:

а) прямая может принадлежать плоскости (условия принадлежности рассмотрены ранее (см. рисунок 1.13));

б) прямая может быть параллельна плоскости;

в) прямая может пересекать плоскость.

Последние два случая рассмотрим подробнее.

2.1 Построение прямой, параллельной плоскости

Из элементарной геометрии известно, что если прямая линия параллельна какой-либо прямой, находящейся в плоскости, то она параллельна этой плоскости. Следовательно, для построения прямой, параллельной заданной плоскости, надо взять в этой плоскости какую-либо прямую и построить ей параллельную.

На рисунке 2.1 через точку К проведена прямая, параллельная плоскости Р. Для этого в плоскости Р взята произвольная прямая MN, и проекции искомой прямой проведены параллельно одноименным проекциям прямой MN.

На рисунке 2.2 через точку С проведена прямая, параллельная плоскости, заданной параллельными прямыми Е и F, и параллельная плоскости проекций V. Для этого в заданной плоскости построена фронталь 1-2, и проекции искомой прямой проведены параллельно соответствующим проекциям этой фронтали.

На рисунке 2.3 решена обратная задача — через прямую ВС проведена плоскость, параллельная прямой L.

Плоскость, образованная пересекающимися прямыми ВС и CD, есть искомая, так как прямая CD проведена параллельно заданной прямой L.

2.2 Построение прямой, пересекающей плоскость общего положения

При решении вопроса о положении прямой относительно плоскости следует помнить, что:

а) прямая параллельна плоскости, если она параллельна какой-либо прямой в этой плоскости;

б) прямая принадлежит плоскости, если проходит хотя бы через две точки, принадлежащие плоскости;

в) прямая пересекает плоскость, если не удовлетворяет первым двум требованиям.

Следуя приведенным выше соображениям, оценим взаимное положение прямой l и плоскости ΔABC, представленных на рисунке 2.4.

Если прямая l принадлежала бы плоскости треугольника, то обе проекции отрезка 11-21 и 12-22 совпали бы с проекциями прямой (рисунок 2.4а). Если бы прямая l и ΔАВС были бы параллельны, то проекции 11-21 и l1 и проекции
12-22 и l2 были бы соответственно параллельны. Так как прямая l и не принадлежит, и не параллельна плоскости, то очевидно, что прямая l пересекает плоскость ΔАВС и имеет с ним общую точку k рисунок 2.4б.

Если прямая общего положения, а плоскость частного положения, то решение вопроса об их взаимном положении не требует дополнительных построений. На рисунке 2.5а прямые l и n параллельны плоскости ΔАВС (n//ab, l//ac), а на рисунке 2.5б пересекают плоскости в точке К.

Рисунок 2.5

Определение видимости участков прямых и плоскостей осуществляется с помощью конкурирующих точек. На рисунке 2.6а изображены горизонтально конкурирующие точки А и В, а на рисунке 2.6б изображены фронтально конкурирующие точки C и D. Горизонтально конкурирующая точка А является видимой на горизонтальной проекции, так как ее фронтальная проекция наиболее удалена от оси Х. На фронтальной плоскости (рисунок 2.6б) видимой является проекция точки D, так как ее горизонтальная проекция наиболее удалена от оси Х.

Рисунок 2.6

На рисунке 2.4 в точке 22 находятся две фронтально конкурирующие точки: одна принадлежит прямой l, вторая — стороне ab. На горизонтальной проекции дальше от оси Х лежит точка, принадлежащая прямой аb.
Это означает, что на фронтальной проекции сторона ab находится сверху прямой l.

2.3 Взаимное положение двух плоскостей

Две плоскости в пространстве могут быть либо взаимно параллельными, в частном случае совпадая друг с другом, либо пересекающимися. Взаимно перпендикулярные плоскости представляют собой частный случай пере-секающихся плоскостей и будут рассмотрены далее.

Из элементарной геометрии известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Иными словами, если плоскости параллельны, то всегда в каждой из них можно построить по две пересекающиеся прямые так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости (рисунок 2.7). Все три плоскости, изображенные на рисунке 2.7, параллельны между собой.

Но такими пересекающимися прямыми могут быть и следы плоскости. Следовательно, если два пересекающихся между собой следа одной плоскости параллельны одноименным следам другой плоскости, то обе плоскости параллельны между собой (рисунок 2.8).

Если хотя бы одна пара одноименных следов двух плоскостей пересекается, то плоскости пересекаются (рисунок 2.9).

Рисунок 2.8 Рисунок 2.9

Если же плоскости заданы не пересекающимися, а параллельными следами (рисунок 2.10), то для решения вопроса, пересекаются они или параллельны, надо построить их следы на третьей плоскости проекций (рисунок 2.11).

Изображенные на рисунке 2.11 плоскости Р и Q пересекаются, а плоскости R и S параллельны.

Рисунок 2.10 Рисунок 2.11

2.4 Построение взаимно параллельных плоскостей

На рисунке 2.12 через точку К проведена плоскость, параллельная плоскости, заданной двумя пересекающимися прямыми АВ и ВС. Искомая плоскость также выражена двумя пересекающимися прямыми, соответственно параллельными заданным.

Рисунок 2.12 Рисунок 2.13

На рисунке 2.13 через точку С проведена плоскость, параллельная плоскости, заданной двумя параллельными прямыми Е и F. Искомая плоскость выражена двумя пересекающимися прямыми, одна из которых проведена параллельно прямым, определяющим заданную плоскость, а вторая — параллельно произвольной прямой 1-2, взятой в заданной плоскости.

На рисунке 2.14 через точку А проведена плоскость Q, параллельная плоскости Р, заданной следами. Для этого через точку А проведена вначале горизонталь AN плоскости (горизонтальная проекция искомой горизонтали искомой плоскости должна быть параллельна РН, определен фронтальный след этой горизонтали, и через фронтальную проекцию п2 проведен фронтальный след QV искомой плоскости. Горизонтальный след QH плоскости проведен из точки а1 параллельно РH (или параллельно горизонтальной проекции горизонтали AN).

2.5 Пересекающиеся плоскости

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, общие для обеих плоскостей, либо одну точку и направление линии пересечения плоскостей.

Перед тем как рассмотреть построение линии пересечения двух плоскостей, разберем важную вспомогательную задачу: найдем точку К пересечения прямой общего положения с проецирующей плоскостью.

Пусть, например, даны прямая а и горизонтально проецирующая плоскость P (рисунок 2.15). Тогда горизонтальная проекция К1 искомой точки должна одновременно лежать на горизонтальной проекции Ph плоскости P и на горизонтальной проекции а1 прямой а, т. е. в точке пересечения а1 с Ph (К1 = а1 ∩ Ph) (рисунок 2.16).

Фронтальная проекция К2 точки К расположена на линии проекционной связи и на фронтальной проекции а2 прямой а.

Рисунок 2.15 Рисунок 2.16

А теперь разберем один из частных случаев пересекающихся плоскостей, когда одна из них – проецирующая.

На рисунке 2.17 приведены плоскость общего положения, заданная ΔАВС, и горизонтально проецирующая плоскость a. Найдем две общие точки для этих двух плоскостей. Очевидно, этими общими точками для плоскостей ∆АВС и α будут точки пересечения сторон АВ и ВС ΔАВС с проецирующей плоскостью a. Построение таких точек D и Е, как на пространственном чертеже (см. рисунок 2.17), так и на эпюре (рисунок 2.18) не вызывает затруднений после разобранного выше примера (см. рисунки 2.15, 2.16).

Рисунок 2.17 Рисунок 2.18

Соединяя одноименные проекции точек D и Е, получим проекции линии пересечения плоскости ∆АВС и плоскости a.

Таким образом, горизонтальная проекция D1E1 линии пересечения заданных плоскостей совпадает с горизонтальной проекцией проецирующей плоскости a (с ее горизонтальным следом a1).

Рассмотрим теперь общий случай. Пусть в пространстве заданы две плоскости общего положения a и b (рисунок 2.19). Для построения линии их пересечения необходимо, как отмечалось выше, найти две точки, общие для обеих плоскостей.

Для определения этих точек заданные плоскости пересекают двумя вспомогательными плоскостями. В качестве таких плоскостей целесо-образнее взять проецирующие плоскости и, в частности, плоскости уровня. На рисунке 2.19 первая вспомогательная плоскость уровня g каждую из данных плоскостей пересекает по горизонталям h и h1, которые определяют точку 1, общую для плоскостей a и b, а значит, и принадлежащую линии их пересечения. Взяв вторую вспомогательную плоскость d, например, также параллельную Н, получим еще одну точку – 2, принадлежащую плоскостям a и b. Эта точка определяется пересечением горизонталей h2 и h3, по которым вспомогательная плоскость d пересекает каждую из данных плоскостей.

Описанный метод применен для эпюрного построения проекций линии пересечения двух плоскостей, первая из которых задана двумя параллель-ными прямыми, а вторая – тремя точками (рисунок 2.20). С помощью вспомогательной плоскости g найдена точка 1 как точка, в которой пересекаются горизонтали h и h1. Точно так же с помощью плоскости d определена вторая точка – 2.

Некоторого упрощения можно достичь, если вспомогательные прое-цирующие плоскости проводить через прямые, задающие плоскость, что и сделано на рисунке 2.21, где построена линия 1–2 пересечения плоскостей a (∆АВС) и b (∆DEF) Точка 1 этой линии определена с помощью фронтально проецирующей плоскости g, проведенной через сторону DЕ треугольника DEF. Именно эта сторона, проекции которой заданы, и является линией пересечения плоскости треугольника DEF и g (DE = b ∩ g).

Видимость сторон треугольника определена с помощью конкурирующих точек. На рисунке 2.21 в точке K2 находятся две конкурирующие точки: одна принадлежит проекции прямой D2E2, а вторая проекции стороны А2С2. На горизонтальной проекции дальше от оси х лежит точка на прямой D1E1. Это означает, что на фронтальной проекции сторона DE находится сверху прямой АС.

Упрощение графического решения в том и состоит, что не нужно чертить эту прямую, входящую в число элементов, задающих плоскость b.

Аналогично, проведя через сторону ВС горизонтально проецирующую плоскость d, найдем точку 2. На рисунке 2.21 прямая ВС = d ∩ a, а MN = d ∩ b. Пересечение этих прямых определяет точку 2. Причем ее фронтальная проекция 22 была построена раньше, чем 21.

Ниже приведем примеры пересечения плоскостей, заданных следами (рисунок 2.22).

Плоскость P – общего положения, плоскость Q – фронтально проецирующая. Линия пересечения 1-2 является прямой общего положения (рисунок 2.22а).

Плоскость Р – общего положения, плоскость Q – горизонтально проецирующая. Линия пересечения 1-2 является прямой общего положения (рисунок 2.22б).

Плоскость Р – общего положения, Q – горизонтальная плоскость уровня. Линия пересечения является горизонталью (рисунок 2.22в).

Плоскость Р – общего положения, Q – фронтальная плоскость уровня. Линия пересечения является фронталью (рисунок 2.22г).

Плоскости Р и S – являются фронтально проецирующими. Линия пересечения является фронтально проецирующей прямой (рисунок 2.22д).

Плоскости Р и Q – общего положения. Но, так как их фронтальные следы параллельны, то пересекаются они по прямой, являющейся фронталью (рисунок 2.22е).

Плоскости Р и Q – общего положения. Линия пересечения является прямой общего положения (рисунок 2.22ж).

Плоскости профильно проецирующие. Линия пересечения – профильно проецирующая (рисунок 2.22з).

В тех случаях, когда одна из заданных пересекающихся плоскостей является плоскостью частного положения, построение линии пересечения их значительно упрощается.

На рисунке 2.23а одна из заданных плоскостей (плоскость ΔDEF) является горизонтально проектирующей. Построение линии пересечения этих плоскостей свелось к построению фронтальных проекций точек 1 и 2, принадлежащих искомой линии. На рисунке 2.23б одна из плоскостей (плоскость ab//cd) является фронтально проецирующей. Построение линии пересечения свелось к построению горизонтальной проекции точек 1 и 2.

2.6 Прямая линия, пересекающая плоскость общего положения

При определении точки пересечения прямой с плоскостью удобно пользоваться вспомогательной секущей плоскостью частного положения. Различают следующие три этапа решения этой задачи:

1) построение вспомогательной плоскости g, которую проводят через прямую а (а Î g);

2) построение линии пересечения n вспомогательной плоскости g и ΔВСD;

3) определение искомой точки К как точки пересечения двух прямых: данной а и построенной n (К = a ∩ n) (рисунок 2.24).

Точно в такой же последовательности решают два примера на эпюре (рисунки 2.25, 2.26). При выполнении эпюрных построений необходимо проявлять особое внимание к последней стадии решения, когда опреде-ляются проекции искомой точки.

Рассмотрим решение примеров. На рисунке 2.25 дано изображение прямой а, пересекающейся с плос-костью ΔВСD.

Точка пересечения К найдена с помощью горизонтально проецирую-щей плоскости g, которая с заданной плоскостью пересекается по пря-
мой n.

Искомая точка К пересечения прямой а с данной плоскостью ΔBCD определена как точка пересе-чения линий а и n.

Следует иметь в виду, что если в качестве вспомогательной плоскости взята горизонтально проецирующая, то первой из двух будет определена фронтальная проекция искомой точки (см. рисунок 2.25). Применяя же фронтально проецирующую плоскость, сначала находят горизонтальную проекцию К1, а затем К2 (см. рисунок 2.26).

Решение задачи на эпюре должно завершиться определением видимых участков на проекциях данной прямой. Видимость прямой а относительно плоскости ΔBCD (см. рисунок 2.25) установлена с помощью специальных лучей, которые мысленно проводят через точки пересечения проекций данной прямой и сторон треугольника (метод конкурирующих точек).

На рисунке 2.27 приведен пример пересечения фронтально проецирующей прямой а с плоскостью общего положения ΔАВС. Для построения точки пересечения К прямая а заключена во вспомогательную фронтально проецирующую плоскость g (плоскость g пересекает ABC по прямой n). Горизонтальная проекция К1 лежит на пересечении n1 и а1. Фронтальная проекция К2 точки К совпадает с фронтальной проекцией а2 прямой.

Рисунок 2.25 Рисунок 2.26

1. Гордон, В. О. Курс начертательной геометрии / , -Огиевский; под ред. изд., стер. — М.: Высшая школа, 2003.

2. Гордон, В. О. Сборник задач по курсу начертательной геометрии / , , ; под ред. . — 9-е изд., стер. — М.: Высшая школа, 2003.

3. Курс начертательной геометрии / под ред. изд, стер. – М.: Выcшая школа, 2002.

4. Начертательная геометрия / под ред. . -7-е изд., перераб. и доп. — М.: Выcшая школа, 2000.

5. Начертательная геометрия. Инженерная и машинная графика: программа, контрольные задания и методические указания для студентов-заочников инженерно-технических и педагогических специальностей вузов / , , ; под ред. . — 2-е изд., испр. — М.: Выcшая школа, 2001.

6. Фролов, геометрия / — М.: Машиностроение, 1978.

7. Бубенников, геометрия / , . – М.: Высшая школа, 1973.

8. Начертательная геометрия / под общей ред. . — Минск: Вышейшая школа, 1967.

9. Боголюбов, : учебник для машиностроительных специальностей средних специальных учебных заведений. – 3-е изд., испр. и доп. – М.: Машиностроение, 2000.

10. Начертательная геометрия: учебник для вузов / , , ; под ред. . – 6-е изд., перераб. и доп. – М.: Высш. шк., 1990. – 240 с.: ил.

11. Алексеева, чертеж плоскости. Взаимное положение плоскостей: методические указания по изучению курса начертательной геометрии для студентов специальностей 120100 всех форм обучения / , . – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 28 с.

1 Плоскость. Способы задания. Прямые и точки плоскости_____________

1.1 Способы задания плоскости___________________________________

1.2 Характерные положения плоскости относительно плоскостей проекций (плоскости частного положения)___________________________

1.3 Прямая и точка в плоскости___________________________________

2 Положение прямых и плоскостей относительно друг друга____________

2.1 Построение прямой, параллельной плоскости____________________

2.2 Построение прямой, пересекающей плоскость общего положения___

2.3 Взаимное положение двух плоскостей__________________________

2.4 Построение взаимно параллельных плоскостей__________________

2.5 Пересекающиеся плоскости___________________________________

2.6 Прямая линия, пересекающая плоскость общего положения________

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ.

ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТИ.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Методические рекомендации по изучению курса начертательной геометрии

для студентов специальностей 151001

дневной, вечерней и заочной форм обучения

Подписано в печать 15.08.2007. Формат 60´84 1/8

Усл. п. л. — 3,48. Уч.-изд. л. — 3,75

Печать — ризография, множительно-копировальный

Источник