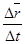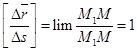Перечислите способы задания движения материальной точки

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Перечислите способы задания движения материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

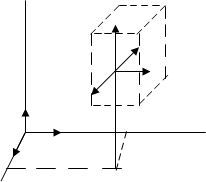
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Способы задания движения.

Кинематика, задачи кинематики

Кинематикой называется раздел теоретической механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.

В ней устанавливаются: 1) классификация движения, 2) основные кинематические величины, характеризующие эти движения, и зависимости между ними (расстояния, скорости, ускорения).

Система отсчета

Непрерывное изменение положения тела А в пространстве с течением времени по отношению к другому телу В называется движением тела А относительно тела В.

С телом, относительно которого будем изучать движение другого тела или точки, свяжем систему координатных осей и назовем ее системой отсчета (движущаяся, условно неподвижная).

Пространство, неизменно связанно с системой отсчета, будем рассматривать как трехмерное, для которого справедлива геометрия Евклида. Время будем считать универсальным, то есть протекающим во всех системах отсчета одинаково. За единицу времени принимается 1 секунда. (Время – скалярная непрерывно изменяющаяся величина).

Кинематика точки.

Способы задания движения.

S

o

Представим (.) М, которая движется в системе отсчета охуz (рис. 1).

z

Рис.1

k

r

z

y

j

x

x

При движении она проходит через различные точки пространства. Множество точек пространства, через которые последовательно проходит точка, называется траекторией движущейся точки.

Если траектория (.) прямая линия, движение точки называется прямолинейным, если траектория (.) кривая, то криволинейным.

Траектория – суть непрерывная линия.

Условимся называть (.) пространства системы отсчета охоу, через которую в данный момент проходит точка, положение движущейся точки в этой системе отсчета в данный момент времени.

Задать движение (.) – это значит указать способ, при помощи которого можно определить положение ее в пространстве в любой момент времени.

Существует 3 способа задания движения точки:

Векторный, координатный, естественный.

Рассмотрим эти способы.

А) Векторный способ задания движения (.) состоит в том, что положение движущейся (.) в пространстве в каждый момент времени определяется радиусом-вектором r, проведенным как правило, из начала координат в данную точку (рис. 1).

Этот радиус вектор в общем случае движения (.) изменяется, как по величине, так и по направлению и является функцией времени.

Равенство (1.1) называется уравнением движения (.) в векторном виде.

Функция r(t) предлагается дважды дифференцируема во времени.

Б) Координатный способ задания движения (.) состоит в том, что положение движущейся (.) в пространстве в каждый момент времени определяется ее координатами (рис. 1). Координаты (.) с течением времени меняются, предлагаются дважды дифференцируемые функции времени.

Равенство (1.2) называется уравнением движения (.) в декартовых координатах.

= х+ y+ z

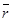
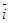
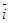
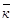
Вспоминая определение траектории (.), заключаем, что уравнения (1.2) представляют собой так же уравнения траекторий (.) в паралитическом виде, в котором параметром является t. Чтобы получить уравнение траектории в координатной форме, надо из уравнений (1.2) исключить время t.

Пример. Движение задано уравнениями:

y=вcos kt+c , где: а,в,с,d-соnst.

Найти уравнение траектории в непараметрическом виде.

Замечаем, что движение происходит в плоскости оху

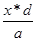
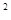
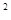
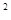
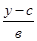
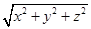
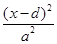
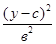
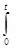
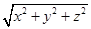
Находим =sin kt ds =dx +dy +dz

=cos kt ds= dt

+ =1 S= dt

Траекторией является эллипс с центром, координаты которого х=-d, у=-с и полуоси а,в.

Замечание. Движение (.)можно задать и в других координатных осях, например полярных, цилиндрических, сферических.

В) Естественный способ задания движения (.) состоит в том, что линия, по которой движется (.) заранее задана, причем ее рассматривают как криволинейную координатную ось, устанавливая на ней начало отсчета и положительное направление на обычной координатной оси. Положение (.) М на этой линии определяется криволинейной координатной,

Которая предполагается дважды дифференцируемой функции времени t.

Равенство (1,3) называется уравнением движения (.) в естественном виде или уравнением движения (.) по траектории.

Следует различать понятия пути П, проходимого (.) и криволинейной координатной S. Криволинейная координата указывает, где находится (.) в данный момент времени; путь П- расстояние, проходимое (.) по траектории за определенный промежуток времени. Криволинейная координата м.б. + и -, т.е. является алгебраической величиной. Путь же (.) – неотрицательная величина.

Основными кин. Величинами, характеризующими движение (.), является ее скорость υ и ускорение

Скорость точки.

V

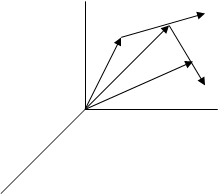
Движение (.) есть непрерывное изменение положения ее в пространстве с течением времени.

М0

М

М0

Z

Последовательные перемещения (.), изображаемые как направленные отрезки, соединяющие любое ее положение с любым последующим, подчиняются правилам сложения векторов. Следовательно, перемещение (.) является векторной величиной.

При изменении времени t перемещение (.) измеряется по модулю и по направлению. Мерой такого изменения перемещения (.) за каждый конечный промежуток времени является средняя скорость – среднее перемещение (.) за единицу времени, т.е.

= = = = и т. д.

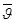
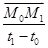
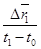
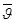
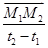
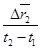
Средняя скорость (.) направлена так же, как перемещение (.) за соответствующий конечный промежуток времени (рис. 2.)

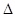
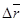
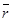
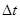
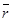
а). При векторном способе задания движения (.) (рис. 3) перемещение (.) из положения, соответствующему любому моменту времени t, за промежуток времени t равно приращению радиуса – вектора, т.е.

= (t+ )- (t)

Средняя скорость (.) на этом перемещении определяется по формуле.

z

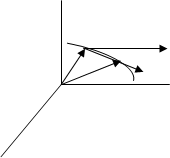
M V рис. 3 =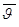

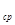
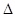
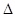
r , t – конечные величины.

Предел средней скорости (.) выражает собой скорость (.) в любой момент времени t и обозначается через υ.

Предел правой части существует, т.к. функция r=r(t) дифференцируема и представляет собой производную от r по t. Следовательно,

= = (1.4.)

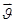
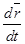
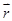
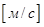
Т. о., мерой движения (.) является скорость (.) При векторном способе задания движения (.) она выражается первой производной по времени от радиуса-вектора (.). Скорость (.) в любой момент времени направлена по касательной к траектории (.) (рис. 3.)

б). Определение скорости (.) при координатном способе задания ее движения. При этом способе движения (.) задано уравнениями:

х=х(t), у=у(t), z=z(t) (рис. 4)

Требуется найти скорость (.).

Будем исходить из определения скорости (m) при векторном способе задания движения

Имеем: = = ( х+ у+ z)?, (1.5.)

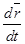
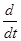
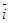
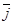
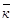
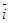
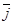
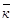
Где: , , — един. векторы коор.осей; x, y, z – координаты движущейся (.).

Проектируем вектора равенства (1.5.) на координатные оси, получим

, , (1.6)

; ; .

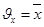
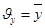
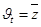
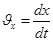
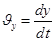
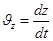
Т.е. проекции скорости (.) на Декарт. Координатные оси выражаются производными по времени от соответствующих координат (.)

Зная ортогональные проекции скорости (.) , находим модуль скорости

= + + ;

= . (1.7)

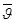
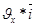
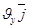
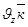
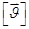
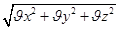
Направление скорости м. определить посредством направляющих конусов.

соs( )= соs ( )= ; cos( )= . (1.8)

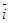
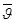
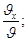
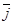
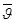
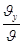
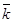
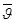
в). Определение скорости (.) при естественном способе задания движения.

Пусть движение (.) задано естественном способом. (рис. 5.)

r рис. 5

Будем исходить из определения скорости (.) при векторном способе задания ее движения. Введем в качестве промежуточной переменной дуговую координату S

= = * = S ,

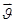
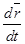
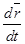
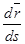
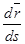
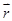
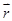
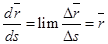
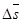
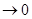
где d s – элементы приращения дуговой координаты, соответствующие элементу перемещения d .(.). Вектор d Направлен по касательной к траектории в данной точке.

— единичный вектор касательной, направленный в «+» направление дуговой оси S

Lim

M

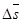
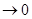
— единичный вектор касательной, направленный в «+» направление дуговой оси S.

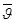
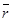
Следовательно, =s (1.9.)

Проектируя вектора равенства (1.9.) на касательную к траектории в данной точке, получим

(1.10)

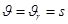
Т.е. проекция скорости (.) на касательную к траектории в данной точке равна производной по времени от дуговой координаты (.)

= =s

Источник